[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Number patterns Decimals Multiplication and divisionMedian
Here you will learn about the median, including what the median is and how to find it.
Students will first learn about the median as part of statistics and probability in 6 th grade.
What is the median?
The median is the middle number of a data set, which is found by arranging the values in ascending order from the smallest value to the highest value and finding the middle value.
For example, find the median:
5 \hspace{0.5cm} 8 \hspace{0.5cm} 10 \hspace{0.5cm} 11 \hspace{0.5cm} 13

The median is 10.
When there is an odd number of values, finding the middle value can be relatively straightforward.
You can use a formula to help you find the position of the median:
\text{median}=(\cfrac{n+1}{2}) \, ^\text{th} \ \text{value}
Where n is the number of values. So when n=5, the median is the 3^\text{rd} value.
\text{position of the median}=(\cfrac{n+1}{2}) \, ^\text{th}=(\cfrac{5+1}{2}) \, ^\text{th}=3^\text{rd} \, \text{value}

However, when there is an even number of values, you get a middle pair. In this case, to find the median you need to find the average or arithmetic mean of the middle pair of values.
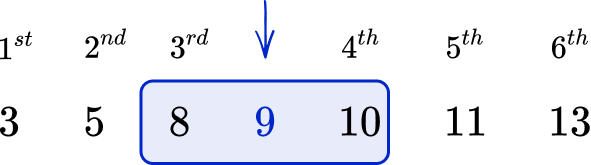
For example, find the median:
3 \hspace{0.5cm} 5 \hspace{0.5cm} 8 \hspace{0.5cm} 10 \hspace{0.5cm} 11 \hspace{0.5cm} 13

The middle pair of values is 8 and 10. The average of 8 and 10 is 9.
You find this by adding the two values together and dividing by 2.
\cfrac{8+10}{2}=\cfrac{18}{2}=9
The median is 9.
You can use a formula to help you find the position of the median:
\text{median}=(\cfrac{n+1}{2}) \, ^\text{th} \ \text{value}
Where n is the number of values. So when n=6, the median is the 3.5^\text{th} value, so the midpoint of the 3^\text{rd} and 4^\text{th} values.
\text{position of the median}=(\cfrac{n+1}{2}) \, ^\text{th}=(\cfrac{6+1}{2}) \, ^\text{th}=3.5^\text{th} \, \text{value}
The median is a measure of central tendency because it describes a set of numbers by identifying a central position or middle point within the data.
What is the median?

Common Core State Standards
How does this relate to 6 th grade math?
- Grade 6 – Statistics and Probability (6.SP.B.5c)
Giving quantitative measures of center (median and/or mean) and variability (interquartile range and/or mean absolute deviation), as well as describing any overall pattern and any striking deviations from the overall pattern with reference to the context in which the data were gathered.
How to find the median
In order to find the median:
- Order the list of numbers.
- Find the middle number.
- Write down the median.
![[FREE] Averages and Range Check for Understanding (Grade 6)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Averages-and-Range-listing-image.png)
[FREE] Averages and Range Check for Understanding (Grade 6)
![[FREE] Averages and Range Check for Understanding (Grade 6)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Averages-and-Range-listing-image.png)
Use this quiz to check your 6th grade students’ understanding of averages and range. 10+ questions with answers covering a range of 6th grade averages and range topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Averages and Range Check for Understanding (Grade 6)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Averages-and-Range-listing-image.png)
[FREE] Averages and Range Check for Understanding (Grade 6)
![[FREE] Averages and Range Check for Understanding (Grade 6)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Averages-and-Range-listing-image.png)
Use this quiz to check your 6th grade students’ understanding of averages and range. 10+ questions with answers covering a range of 6th grade averages and range topics to identify areas of strength and support!
DOWNLOAD FREEMedian examples
Example 1: odd number of values
Find the median of this set of data:

- Order the list of numbers.
The list of numbers is not in order, so you need to put the numbers in ascending order from smallest value to largest value.

2Find the middle number.
To find the middle number, you can count in from the bottom and the top of the list.

3Write down the median.
The median value is 11.
Alternatively there is a formula you can use to find the position of the median.
\text{median}=(\cfrac{n+1}{2}) \, ^\text{th} \, \text{value}
Where n is the number of values. So when n=5, the median is the 3^\text{rd} value.
\text{position of the median}=(\cfrac{n+1}{2}) \, ^\text{th}=(\cfrac{5+1}{2}) \, ^\text{th}=3^\text{rd} \, \text{value}

The median is 11.
Example 2: odd number of values
Find the median of the following data:

Order the list of numbers.
The list of numbers is not in order, so you need to put the numbers in ascending order from smallest value to largest value.

Find the middle number.
To find the middle number, you can count in from the bottom and the top of the list.

Write down the median.
The median is 10.
Alternatively, there is a formula you can use to find the position of the median.
\text{median}=(\cfrac{n+1}{2}) \, ^\text{th} \, \text{value}
Where n is the number of values. So when n=7, the median is the 4^\text{th} value.
\text{position of the median}=(\cfrac{n+1}{2}) \, ^\text{th}=(\cfrac{7+1}{2}) \, ^\text{th}=4^\text{th} \ \text{value}

The median is 10.
Example 3: odd number of values
Find the median:

Order the list of numbers.
The list of numbers is not in order, so you need to put the numbers in ascending order from smallest value to largest value.

Find the middle number.
To find the middle number, you can count in from the bottom and the top of the list.

Write down the median.
The median is 9.
Alternatively, there is a formula you can use to find the position of the median.
\text{median}=(\cfrac{n+1}{2}) \, ^\text{th} \, \text{value}
Where n is the number of values. So when n=9, the median is the 5^\text{th} value.
\text{position of the median}=(\cfrac{n+1}{2}) \, ^\text{th}=(\cfrac{9+1}{2}) \, ^\text{th}=5^\text{th} \, \text{value}

The median is 9.
Example 4: even number of values
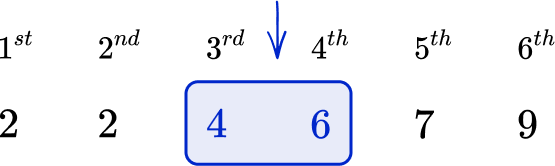
Find the median:

Order the list of numbers.
The list of numbers is not in order, so you need to put the numbers in ascending order from smallest value to largest value.

Find the middle number.
To find the middle number you can count in from the bottom and the top of the list.

Since there is an even number of values, you have a middle pair. You need to find the arithmetic mean, or average, of this middle pair.
\cfrac{4+6}{2}=\cfrac{10}{2}=5
Write down the median.
The median is 5.
Alternatively, there is a formula you can use to find the position of the median.
\text{median}=(\cfrac{n+1}{2}) \, ^\text{th} \, \text{value}
Where n is the number of values. So when n=6, the median is the 3.5^\text{th} value.
This would be the average of the 3^\text{rd} and 4^\text{th} values.
\text{position of the median}=(\cfrac{n+1}{2}) \, ^\text{th}=(\cfrac{6+1}{2}) \, ^\text{th}=3.5^\text{th} \, \text{value}
The median is 5.
Example 5: even number of values
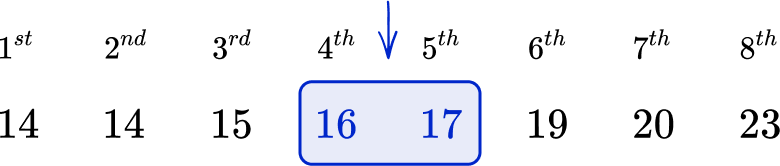
Find the median:

Order the list of numbers.
The list of numbers is not in order, so you need to put the numbers in ascending order from smallest value to largest value.

Find the middle number.
To find the middle number you can count in from the bottom and the top of the list.

Since there is an even number of values, you have a middle pair. You need to find the arithmetic mean, or average, of this middle pair.
\cfrac{16+17}{2}=\cfrac{33}{2}=16.5
Write down the median.
The median is 16.5.
Alternatively, there is a formula you can use to find the position of the median.
\text{median}=(\cfrac{n+1}{2}) \, ^\text{th} \, \text{value}
Where n is the number of values. So when n=8, the median is the 4.5^\text{th} value.
This would be the average of the 4^\text{th} and 5^\text{th} values.
\text{position of the median}=(\cfrac{n+1}{2}) \, ^\text{th}=(\cfrac{8+1}{2}) \, ^\text{th}=4.5^\text{th} \, \text{value}
The median is 16.5.
Example 6: even number of values
Find the median:

Order the list of numbers.
The list of numbers is not in order, so you need to put the numbers in ascending order from smallest value to largest value.

Find the middle number.
To find the middle number you can count in from the bottom and the top of the list.

Since there is an even number of values, you have a middle pair. You need to find the arithmetic mean, or average, of this middle pair.
\cfrac{8+11}{2}=\cfrac{19}{2}=9.5
Write down the median.
The median is 9.5.
Alternatively, there is a formula you can use to find the position of the median.
\text{median}=(\cfrac{n+1}{2}) \, ^\text{th} \, \text{value}
Where n is the number of values. So when n=10, the median is the 5.5^\text{th} value.
This would be the average of the 5^\text{th} and 6^\text{th} values.
\text{position of the median}=(\cfrac{n+1}{2}) \, ^\text{th}=(\cfrac{10+1}{2}) \, ^\text{th}=5.5^\text{th} \, \text{value}

The median is 9.5.
Teaching tips for median
- Provide a real-life scenario where the median can be applied. For example, you can talk about finding the median age or median income of a group of people or the median score in a sports tournament. This helps students understand the relevance of the concept.
- Talk about how outliers can affect the median. Explain that outliers are extreme values that are significantly different from the other values in a data set. Show examples where removing or including outliers can change the median value.
Easy mistakes to make
- Not placing numbers in ascending order
Check that the list of numbers is in numerical order before finding the median number.
- Thinking that the median must be a number shown in the data set
The median can be a number that is not in the original data set.
When there is an odd number of values, the median is one of the original values.
When there is an even number of values, it is acceptable that the median is NOT one of the original values.
- Confusing median with mean or mode
The mean is the average of all the values, the median is the middle value, and the mode is the most frequently occurring value(s) in a data set. Each measure provides different information about the data and is useful in different scenarios.
Related averages and range lessons
- Averages and range
- Mean median mode
- Mean in math
- Mode in math
- Range in math
Practice median questions
1. Find the median.
![]()




Put the numbers in ascending order from the smallest value to largest value. Then find the middle value.
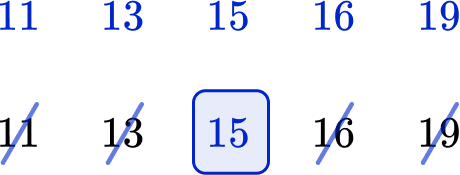
The middle value is 15, so this is the median.
2. Find the median.
![]()




Put the numbers in ascending order from the smallest value to largest value. Then find the middle value.
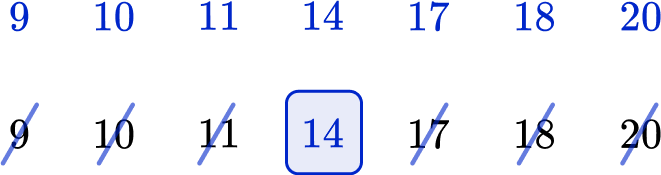
The middle value is 14, so this is the median.
3. Find the median.
![]()




Put the numbers in ascending order from the smallest value to largest value. Then find the middle value.

The middle value is 18, so this is the median.
4. Find the median.
![]()




Put the numbers in ascending order from the smallest value to largest value. Then find the middle value. Since this data set has an odd number of observations, we need to find the mean of the middle pair of values.

The middle pair of values are 20 and 23. The average of these is 21.5. The median is 21.5.
\cfrac{20+23}{2}=\cfrac{43}{2}=21.5
5. Find the median.
![]()




Put the numbers in ascending order from the smallest value to largest value. Then find the middle value. Since this data set has an odd number of observations, we need to find the mean of the middle pair of values.
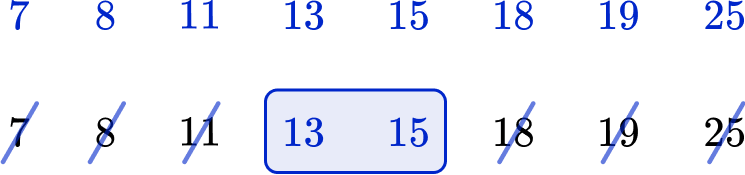
The middle pair of values are 13 and 15. The average of these is 14. The median is 14.
\cfrac{13+15}{2}=\cfrac{28}{2}=14
6. These are the heights, in meters, of members of a water polo team. Find the median height of the 7 players.
![]()




Put the numbers in ascending order from the smallest value to largest value. Then find the middle value.

Median FAQs
The median is the middle number of a data set, which is found by arranging the values in ascending order from the smallest value to the highest value and finding the middle value.
To find the median of a data set with an even number of data points, you need to find the average or arithmetic mean of the middle pair of values.
Descriptive statistics are used to summarize or organize a data set. Some common descriptive statistics are mean, median, mode, and range.
In geometry, the median refers to a line segment that connects a vertex of a triangle or a polygon to the midpoint of the opposite side. It divides the shape into two equal parts.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!