20 Math Strategies Proven To Improve Progress And Understanding

Working with thousands of students every week, we’ve developed a clear schema of math strategies that really make an impact on math students’ achievement and progress in math across grade levels, from elementary school to high school.

These math strategies are drawn from the most effective teaching strategies we believe you need when teaching math.

Here at Third Space Learning, we have delivered online math tutoring to over 100,000 students across 3,000 schools. Every lesson is taught by professionally trained math tutors working one-on-one with the learners.

Origins of our math approach

As part of our quality control and to ensure the best outcomes for every child, we realized early on that we needed a clear framework for our tutors to follow – a rubric that identifies the ‘Third Space Learning’ approach.

So, drawing on what we know about quality first teaching and a math mastery approach, as well as the specific requirements of online tutoring and tutoring in a one-to-one environment, this is the list of what we believe to be crucial in math, and indeed, what every subject leader or teacher involved in teaching math should be aware of.

We hope that it proves to be valuable in helping you to reflect on your own math practice and that there will be an idea here that you can take to further support your own students with math.

Why are these strategies important in math?

Excellence in math depends on a combination of factors – the right math resources, good quality teaching and progress monitoring backed up by regular professional development, strong subject leadership in the school from the math coordinator, and a whole school math curriculum and progression from kindergarten onwards that teachers understand and feel ownership of.

One of the joys of math (unlike other subjects like History or Geography) is that each piece of new knowledge builds on prior knowledge.

Provide children with the building blocks of place value, and explain to them the value of learning their number bonds, and by the time you get to addition problems and subtraction at elementary school, much of the cognitive load of learning a new technique like standard algorithm subtraction will be lifted.

Similarly, without a good grasp of multiplication charts, they will find long division, fractions and even pie charts, significantly harder.

With a whole school approach, the child’s learning journey in math can progress logically from early numeracy through to the more sophisticated calculations and reasoning they make as they are ready to transition from elementary school to middle school and beyond.

Read more:

• 8 Common Core math examples
• 18 FREE math intervention resources
• Math strategies for problem solving

The list of math strategies

These are the math strategies and math intervention strategies we use to ensure progression through every tutoring lesson we deliver.

1: Build interest and rapport

Nothing captures a student’s imagination more than their own interests! While learning your students’ hobbies and favorite pastimes can be time-consuming, it should happen naturally over the course of the year. You can then use this knowledge to personalize classroom explanations and make it more interactive.

Our 1-on-1 math specialist tutors prepare for each lesson by thinking about how they can effectively engage students and relate content to their interests and use images related to these to personalize the session. It’s simple, but it’s also a great way to turn a new concept from ‘mundane’ to ‘memorable’ and to improve students’ impressions of math class!

Don’t think this is only a strategy for the elementary math classroom- this is equally effective in middle school and high school classrooms. While you cannot personalize for every child, engaging students with fun real life math activities is a great start.

2. Know your students and your resources

Differentiation and differentiated instruction should be the bread and butter of teaching for interventions (and in general). If you’re not sure if a math resource is pitched at the right level for your student(s), then you need to find out. Without appropriate differentiation in the classroom, time spent on a resource could well be time wasted.

Before your intervention, look at previous session data or student profiles. Are there any areas you should be aware of, such as ELL, dyscalculia, etc?

Like our tutors, we advise you tally this against the intervention resources and make notes against any potential areas of difficulty, or likely misconceptions. Remember, forewarned is forearmed and avoiding speed bumps when time is limited is crucial to maximizing learning.

With a class of up to 30 students, it can be more tricky to ensure you’re aware of every misconception. We recommend using diagnostic assessments wherever possible at the start and end of every topic. See also this blog post on effective mixed ability grouping in math.

3. Recap prior learning

Particularly in math, where learning needs to build upon previous learning and foundation concepts, recapping prior knowledge through retrieval practice or other methods is essential.

When teaching students through our specialist math intervention, our tutors always create a linking question from past lessons to activate students’ math skills and kick-start learning a new one.

This can save precious time and ensure you never try to teach a new concept to a class that they’re simply not ready for.

4. Share lesson objectives to improve math progress

Don’t assume that just showing your class the learning objectives will make them understand them. Our tutors do this by; asking students to identify keywords they don’t understand, and asking open ended questions such as ‘what is the difference’ and ‘what do you think of’, and discussing how the lesson objectives link to prior learning. This makes the thought processes of the student ‘visible’ to the tutor.

Discussing lesson objectives is much better for long term memory retention than just stating them.

5. Teach key math vocabulary

If a student does not understand key math vocabulary, it is important to get them up to speed before undertaking new learning. To address any misunderstanding, our tutors will often get students to describe mathematical terms in their own words before they start the math instruction of a new topic.

Plus if students are struggling they will simplify keywords and, for example, discuss ‘sharing’ instead of ‘division’.

6. Use AfL to adjust pitch and pace

Where possible, learning should be paced to the needs of the student(s). The last thing any teacher wants is to find that they have moved too quickly through a topic and caused cognitive overload in their student(s).

New to cognitive load theory? Read Clare Sealy’s post on the topic to find out more about this valuable educational psychology tool, with a focus on how it impacts elementary school students.

This is why our tutors use assessment for learning and formative assessment strategies to adjust the pitch and pace of their lessons.

This is as simple as moving quickly through content that the student understands, and slowing down to expand or explain a concept that they’re not getting.

The key element is not to move on from content that a student is yet to secure, regardless of how much time you spend on it.

7. Personalize learning and link questions to students’ interests

Personally relevant problems are way more fun to solve. Posing a question in the context of the student’s name, or their favorite animal, is likely to increase their engagement.

To this end, our tutors often use the student’s name, favorite animal, or interests to create personally relevant math problems for them to solve. As familiarity and rapport with your class builds throughout the year, this should become easier and easier to do.

We’ve got plenty of math activities you can use to personalize learning to students’ interest such as these math activities about notable female mathematicians throughout history and more modern examples of famous female mathematicians for International Women’s Day.

8. Create more opportunities for student talk

Finding time for high quality math talk class is hard. But, wherever possible, you should encourage active learning and promote discussion rather than lecturing.

Short attention spans are an ever-present hurdle and classroom discussion keeps students from zoning out. Plus it enhances metacognitive development.

Remember, however, that direct or explicit instruction is still often your most valuable teaching method. Student talk should come after you’ve covered the fundamentals of a topic, not before. Student talk can help you as a teacher to assess students’ understanding and mathematical thinking and adapt your instructional strategies as necessary. 

9. Use ‘Concrete Representational Abstract’ method

The CRA Concrete Representational Abstract method is a staple of many math teachers’ toolkit. Use real objects to build the students’ foundations for conceptual understanding, and follow up with visual representations that help them freely conceptualize a problem.

This technique is tried and tested and not just for low ability students; using it enables all students to grasp more challenging content quickly and effectively.

10. Use variation to improve math progress

There are two stages of this. Conceptual variation, which shows students different ideas that underpin a mathematical concept, can be framed using questions such as ‘what’s the same?’ and ‘what’s different?’ between different representations. It helps students distinguish the essential and obscure characteristics of a math concept.

Procedural variation, which is more useful for multi-step operations and comparing successive procedures (e.g. calculating two different sets of numbers), can be framed as questions such as ‘what do you notice?’ and ‘is there a relationship between?’

11. Frame questions in a real world context

Connecting topics to math in the real world makes them more memorable and engaging. This should be done as often as possible and our tutors are expected to connect all math learning to real life, even in more abstract topics!

For example, if a tutor is teaching rounding up to 1 million, they may look at different populations in towns or cities or ask students to round up the total of people in their hometown.

12. Vary approaches to questions

There’s a big difference between learning a method and gaining real understanding.

Our tutors always teach multiple ways to approach the same problem. For example, when teaching rounding, tutors can use a number line, or ask students to simply use the relevant columns to inform their rounding.

They also make frequent use of goal-free problems and open-ended questions to ensure students learn the underlying concept, rather than simply performing back what they have seen.

13. Move from scaffolding to independent practice

Learning strategies should be structured with gradually decreasing support: from scaffolding to independent learning and finally to stretching. In our intervention, tutors always model answers and show students the steps to success before asking them to answer a question.

Moreover, when moving towards the plenary of a lesson, our tutors provide multiple opportunities for students to work independently and extend their own learning.

Read more

• How to Stretch and Challenge More Able Students
• The 21 Best Math Challenges To Really Stretch Your More Able Elementary School Students

14. Use deeper questioning strategies to help students progress in math

We all know verbal reasoning plays a large part in improving metacognition, but it is the quality of a discussion that counts, not the quantity!

Like our tutors, you can encourage quality student talk by questioning in the classroom in math like ‘how did you get to this answer?’ and ‘how would I extend this question?’ 

15. Use bar-modeling techniques

Bar-modeling is taking the math world by storm for a reason. From routine calculations such as 4 + 3, to more complex multi-step reasoning problems, bar models are a fantastic learning aid as they show the inner workings of math problems.

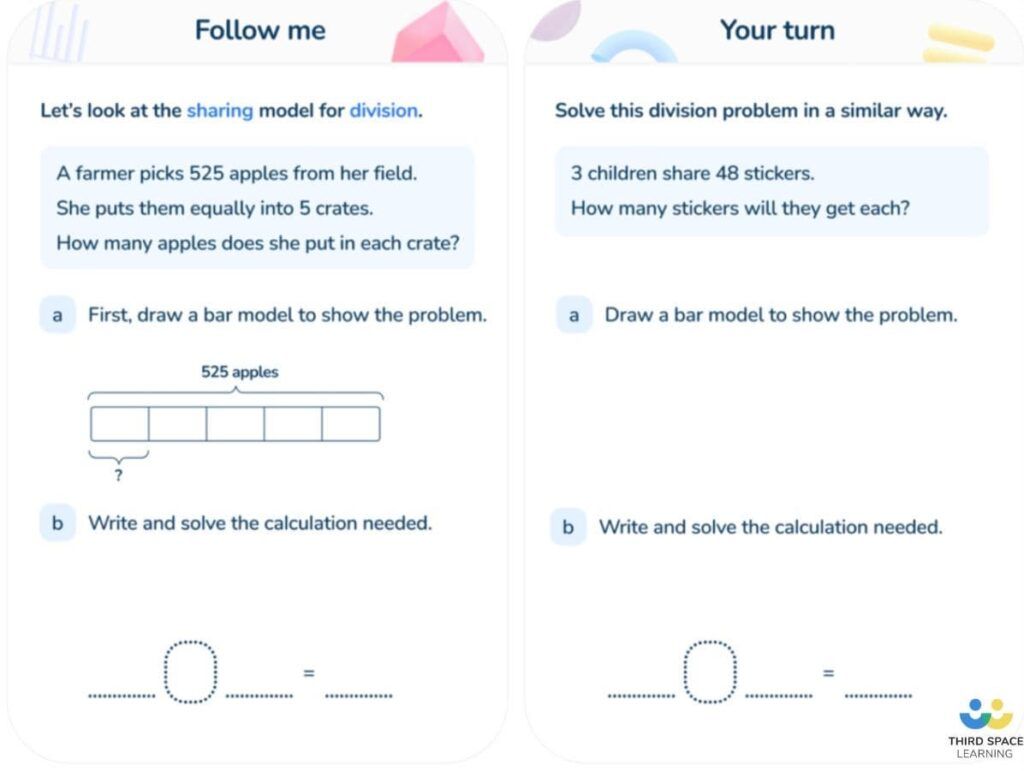
16. Nurture a growth mindset to nurture math progress

Research clearly demonstrates that, compared to other subjects, students are most likely to believe they won’t succeed in math. To build that crucial confidence our tutors always praise the effort a student puts in, rather than the student.

We find phrases like ‘you found a really good way to do that!’, or ‘I can tell you’ve been practicing’, really improve motivation and attitude towards math.

Read more on how to get growth mindset right in schools.

17. Provide a range of strategies and next steps

Just as linking from previous concepts gives students a sense of familiarity, linking to future concepts ensures that students don’t get “lost” in learning. This is why our tutors always signpost the learning in any given lesson.

Signposting can be as simple as telling students that ‘we’re going to move on to rounding numbers to a million, it’ll use the same strategies as rounding to ten thousand, but it’s more of a challenge’. This keeps students engaged and on track.

It’s particularly important when developing reasoning skills.

18. Encourage metacognition to encourage math progress

Metacognition should be an integral part of lessons and students should frequently be assessing their own learning using metacognitive strategies and other thinking skills.

One way to do this is to focus the plenary on what was learned that day and, more importantly, how it was learned. When a child can reflect on their own understanding, what they found more challenging or easier, then you will be starting to achieve metacognition in the classroom.

19. Reward, praise and encourage the student

Praise is a great confidence-builder, and corrections can be incorporated constructively within praise. For example, ‘it’s okay that you’ve made a mistake but it’s important that you learn from it. This is especially crucial with students who may have less math confidence than their peers and those struggling with math anxiety.

20. Teach the teacher

To be effective, student talk requires proper structure and expectations. One technique we use is to ask a student to teach back to the tutor (towards the end of the lesson). It is the ultimate test of understanding.

It’s a particularly effective strategy in 1-to-1 settings, where the student is under less pressure than in a group. However, when used as a group activity (with more confident students doing the teaching) it can be effective in a classroom setting.

If you’re new to this one, at the elementary school level, why not start by trying it to help your students memorize their number facts.

Those are the 20 math strategies that underpin our interventions.

Read more: 9 Tutoring strategies to boost learning

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?