Direct Instruction & Learning From Rosenshine Principles Of Instruction: ‘How I Wish I’d Taught Math’
Clare Sealy looks at the value of explicit and direct instruction in teaching elementary school math and the importance of understanding Rosenshine’s Principles of Instruction to break down teaching into smaller steps.
This article is part of a series published to help elementary school teachers and leaders implement some of the insights and teaching techniques derived from Craig Barton’s bestselling book How I Wish I’d Taught Math. Links to the other 5 articles appear at the end.
This is the second in a series of blog posts inspired by Craig Barton’s book How I Wish I’d Taught Math. If you haven’t already, read the introduction which investigates how cognitive load theory affects elementary school students.
After reading the first blog, we know how easy it is to inadvertently prevent learning by overwhelming working memory through cognitive overload. We can now look further at some teaching methods for avoiding this in elementary school math, the principal of which is direct instruction.
- What is direct instruction?
- Rosenshine’s Principles of Instruction
- 5 key principles of direct instruction for teaching Math
- What does explicit direct instruction look like?
- Elementary school teaching strategies – worked examples using direct instruction in math
- Elementary school teaching strategy – no questions, no checking for understanding
- No talking while modeling
- Words and pictures at the same time are fine
- Supercharged worked examples
- The self-explanation effect
- Supercharged worked examples in an elementary school math context
- The difference with supercharged worked examples
Discovery learning and investigations in math
Craig used to believe that rich tasks such as investigations where children discovered relationships for themselves were more effective teaching strategies than telling children explicitly how to do things.
Discovering was, in his opinion, more creative, required more imagination, was more interesting and much more likely to result in children really understanding the math conceptually, rather than just regurgitating a procedure.
However, Craig now strongly believes that while math investigations have their place, they are completely inappropriate for the initial stage of learning, when children are encountering a concept for the first time. If we want children to become independent problem-solvers, we need to carefully and explicitly teach them new material.
Counter intuitive as it may seem, children do not become independent problem solvers by independently solving problems.
What is direct instruction?
It turns out that there is a lot of research that shows that teaching is much more effective when the teacher explicitly explains material in small, carefully thought out steps, giving children lots of opportunity to practice specific skills before going onto the next small step.
This is particularly true in the early knowledge acquisition phase of learning.
Rosenshine’s Principles of Instruction
If you’re not familiar yet with Rosenshine’s Principles of Instruction, it’s worth taking the time to read his original document – follow the links at the end.
He notably created a list of 10 research-based principles from cognitive science to use in teaching, together with practical strategies for how to implement these in the classroom:
- Begin the lesson with a review of previous learning.
- Present new material in small steps.
- Ask a large number of questions (and to all students).
- Provide models and worked examples.
- Practice using the new material.
- Check for understanding frequently and correct errors.
- Obtain a high success rate.
- Provide scaffolds for difficult tasks.
- Independent practice.
- Monthly and weekly reviews.

5 key principles of direct instruction for teaching Math
Of these ten, Craig particularly focuses on these:
1. Present new information in small steps with student practice after each step
2. Ask a large number of questions and check the response of all students
3. Provide models
4. Guide students through deliberate practice
5. Provide scaffolds for difficult tasks
Craig also cites research from Coe et al (2014) entitled What Makes Great Teaching and the 2014 Center for Education and Statistics report, What works best: evidence-based practices to help improve NSW performance, both of which reach similar conclusions.
What does explicit direct instruction look like?
Direct instruction does not mean boring the pants off children by droning on and on in a math lesson.
Explicit instruction elicits a great deal of student involvement, arguably more than in ‘discovery’ type approaches where some pupils can hide their non-involvement.
This elementary school teaching technique involves lots of questioning in the classroom and guided practice. It is not a one-way lecture, but it is firmly and unapologetically teacher led.
Alternatively, if we try to facilitate children to discover mathematical relationships for themselves, their finite working memories are likely to become overloaded. The information-processing demands of such approaches is very high; too high.
As a result, children often do not learn much from this teaching, despite our best intentions. Even worse, they may learn a misconception, so they actually leave the lesson worse off than when they arrived.
The direct instruction model, on the other hand, breaks learning down into small, readily processed steps.
Elementary school teaching strategies – worked examples using direct instruction in math
The backbone of explicit direct instruction in elementary math is the worked example; that is to say a step-by-step demonstration of how to solve a problem.
“Not that ground-breaking,” I hear you say. “All math teachers use worked examples; they are the bread and butter of our trade.”
But Craig has a very clear process: the use of Example-Problem Pairs.
What this involves is:
- First split the whiteboard in two (headed Worked Example and Your Turn)
- On the left, the teacher works through an example. (In a primary context, this will usually involve using concrete or pictorial representations alongside abstract ones.)
- After having explained this, children copy down this example into their notebooks or journals so that they can refer to it later, and also get practice setting it up correctly.
- On the right is a mathematically, almost identical example for students to try themselves immediately after.
- The teacher then circulates to help anyone who is struggling.
- If the majority of the class is stuck, the teacher stops the class to unpack the misconception, but otherwise children then go on to work through a series of very carefully chosen, structurally similar examples for independent practice.

Elementary school teaching strategy – no questions, no checking for understanding
This might not seem that revolutionary.
However, what I deliberately left out is that during the explanation, the teacher does not stop and ask questions or check for understanding. Students watch and listen in silence.
The reason for this is that questions break up the clarity of the explanation, diverting students’ attention down side streams and away from the crucial focus of the lesson.
Questions are very important at other stages of teaching; prior to teaching something, for example, to check that the required prior knowledge is secure, or later on, once pupils have had a decent stretch of time practicing what has been taught. But not at that fragile point when new knowledge is being introduced.
Cluttering up the working memory with distractions at this delicate stage must be avoided at all costs! So you should avoid asking children mid-explanation questions such as ‘so what comes next?’.
You want working memory focused on what you are teaching, and that alone.
This is not to say that these sorts of questions don’t have their place. There is a significant role for metacognition in the classroom, but it, like many other quality first teaching strategies, is best utilized after the initial explanation stage.
No talking while modeling
In fact, while modeling, do not talk at all at first. Instead, pause briefly between each step, so students have a chance to think about what you have just done. Only once you have finished writing your method on the board should you narrate what you have been doing.
The reason for this is due to something called the split-attention effect.
If students must listen to someone talking at the same time as reading something on the board, then their attention is split – the spoken and the written information compete for attention.
Whereas, if the information is presented in written form first, and then given a clear explanation, this conflict (and the associated increased cognitive load) is avoided.
Words and pictures at the same time are fine
Interestingly, this split-attention effect does not happen if words and pictures are presented at the same time, as the working memory has two ‘channels’ by which it receives information, a visuospatial channel and a phonological channel.
Working memory gets overloaded if too much information flows into one channel, but can cope perfectly well if the information is split between the two.
Written text and speech both use the phonological channel, so should not be used simultaneously. Images however use the visuospatial channel, so do not compete with text – or spoken information – for attention.
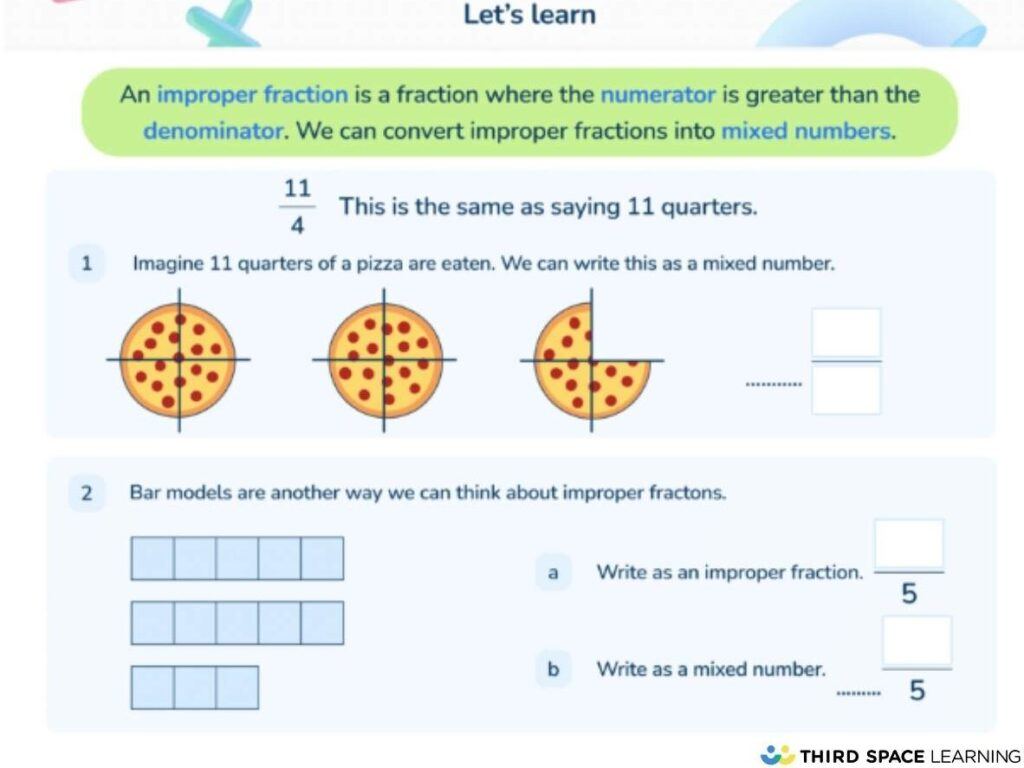
Further vindication of using the math manipulatives approach!
Supercharged worked examples
A further development of this example-problem-pairs approach involves incorporating opportunities for children to try to explain the math to themselves.
Hang on a moment! Isn’t this just the discovery learning type approach just repudiated?
The crucial difference between children explaining their own learning and this approach, is that here, the student is explaining the teacher’s reasoning, not their own, possibly faulty reasoning. This is known as the self-explanation effect.
The self-explanation effect
The self-explanation effect is a potentially powerful technique that involves giving students time – after teacher-led explanation – to try to make sense of information by themselves. It does not involve students explaining things to each other or even talking out loud.
It is giving children the time and space to reflect and begin to make sense of what they have just been taught, one step at a time. The teacher simply pauses after each step so that children can ask themselves: why does this step follow from the previous one?
As children do this, they begin to organize the knowledge in their long-term memory by making links. Seigler (2002) found that children who explained the experimenter’s reasoning learned more than children who explained their own reasoning.
What is more, Seigler also found that explaining why correct answers are correct and incorrect answers are incorrect yielded greater learning than only explaining correct answers.
The timing of this self-explanation is very important for it to be effective.
In super charged worked examples, the teacher outlines a step which children then copy into their notebooks or journals, before being given a prompt to help them think about the math behind the procedure.
Supercharged worked examples in an elementary school math context
Here’s an example of how you might progress through a super-charged worked example as part of a lesson plan. Note that for elementary I wouldn’t recommend writing out the reflection column – it is more for the teacher to use to prompt herself.
Please also note that this is a generic supercharged worked example; you will still need to apply differentiation in the classroom to ensure all your students can follow it, even your low-ability students.
Consider the calculation
653 – 228
Read more: differentiated instruction
Supercharged worked example: Stage 1
The teacher lays out 653 on the board using place value counters on a place value grid in silence and then explains
‘I’ve put 6 hundred counters in the hundreds column, 5 tens counters in the tens column and 3 ones counters in the ones column.’
After a pause, she asks
‘why did I put 5 tens in the tens column?’
Children do not answer or write anything down; they just think.
After a studied pause, the teacher continues her explanation. They point to the 3 then refer back to the written calculation, pointing to the 8. The teacher then starts to subtract counters, silently counting to herself as she does so, giving up and looking frustrated when she ‘realizes’ she can’t get beyond subtracting 3 at this point. She puts the 3 counters back and says
‘I’m not going to do any calculating yet because I can’t subtract 8 from 3’
Next, she asks a question
‘Why can’t I do any calculating yet?’
Again the children do not say anything, they just think about why this might be the case.
Then she continues.
She conspicuously looks at the tens column and ponders for a bit. Then takes one of the ten place value counters and exchanges it for ten one place value counters. After a pause she asks,
‘Why did I exchange one ten for ten ones?’
She then places the exchanged ones in the ones column.
‘Why did I move the counters over to the ones column?’
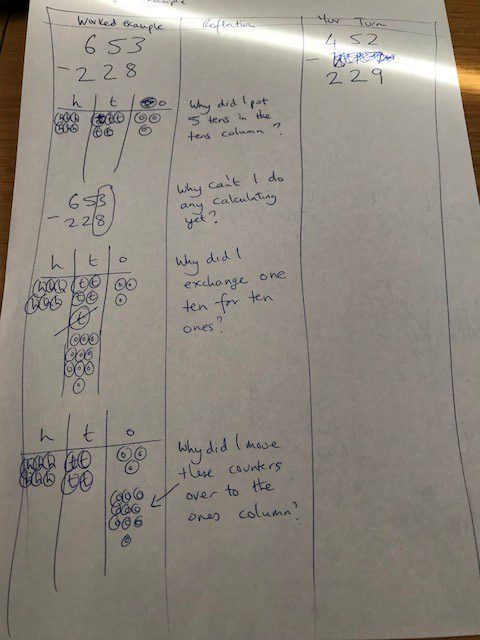
(reflection column for teacher use only – not intended to be seen by students)
Supercharged worked example: Stage 2
She then takes away 8 ones from the thirteen ones in the ones column, leaving 5 ones.
‘Why did I subtract 8 ones?’
She then turns to the tens column, looks at the remaining 4 tens, points back to the written algorithm and points at the written 2.
‘Why am I looking at the 2 digit?’
She then takes away two ten place value counters from the four in the tens column.
She then silently counts how many counters are in the hundreds column and then points to the 2 in the hundreds column in the written algorithm.
‘Why am I checking both digits before I do anything else?’
She then takes away 2 hundreds counters from the 6 in the hundreds column. She then writes then answer 425 after the equals sign in the written algorithm.
‘Why is my answer 425?’
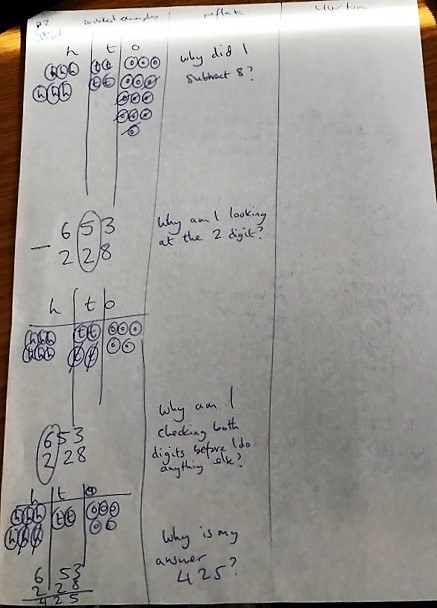
(reflection column for teacher use only – not intended to be seen by students)
The difference with supercharged worked examples
Supercharged worked examples might seem not so different from the elementary school teaching strategies Craig used to use; asking questions in the middle of explaining something, something he now thinks is ineffective. So what is the difference here?
- Children have to answer the question silently, in their own heads, rather than listen to each other’s explanations.
- The pace at which this happens is much more considered. They take longer than ordinary worked examples, and are better off a little way into a topic, once the children know a bit about what they are doing and so are better placed to self-explain.
Read more: Student Centered Learning: A Teacher’s Guide
Other articles in the How I Wish I’d Taught Elementary Math series
- Goal Free Problems And Focused Thinking: How I Wish I’d Taught Primary Math (3)
Sources of inspiration for this article
- Rosenshine, B. (2012) ‘Principles of instruction: research-based strategies that all teachers should know’, American Educator 36 (1) pp.12-39
- Coe, R., Aloisi, C., Higgins, S. and Major, L.E. (2014) What Makes Great Teaching
- Centre for Education and Statistics (2014) What works best: evidence-based practices to help improve NSW performance,
- Seigler, R.S. (2002) ‘Microgenetic studies of self-explanation’ in Granott, N. and Parziale, J. (eds) Microdevelopment: transition process in development and learning. Cambridge University Press pp.31-58
Read more:
- The Learning and Memory in the Classroom: What Teachers Should Know
- When And How To Implement A Spiral Curriculum
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Why not learn more about how it works?
The content in this article was originally written by primary headteacher Clare Sealy and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.




