Developing Math Reasoning In Elementary School And Beyond: The Mathematical Skills Required And How To Teach Them

April 24, 2024 | 4 min read

John Bee

Developing math reasoning skills in elementary school is crucial to succeed in developing a math mastery approach to learning which will support development through to middle school and high school. Students need strong applied reasoning alongside their math skills to be able to succeed – there’s no point in memorizing a theorem if you don’t know when to use it!

The Ultimate Guide to Problem Solving Techniques

Help your students to develop their problem solving skills with this free worksheet.

Download Free Now!

My approach to elementary school level math teaching and learning is that it should be about exploring, reasoning and challenging thinking, rather than learning rote/abstract rules for calculations and facts.

Though I recognize that fluency in math and memorizing key number facts is essential in elementary school mathematics to acquire the basics – these are the prerequisite skills that ought to be used and applied in real life contexts.

To succeed on standardized tests, it is clear that children require deep knowledge of facts and mathematical concepts. Moreover, they need to be able to use and apply these facts to a range of contexts, and different types of word problems, including the more complex multi-step and two-step word problems

What is reasoning in math?

Let’s start with the definition of math reasoning. Reasoning in math is the process of applying logical and critical thinking to a mathematical problem in order to make connections to work out the correct strategy to use (and as importantly, not to use) in reaching a solution.

Reasoning is sometimes seen as the glue that bonds students’ mathematical skills together; it’s also seen as bridging the gap between fluency and problem solving, allowing students to use their fluency to accurately carry out math strategies for problem solving.

In my opinion, it is only when we teach children to reason and give them the freedom to look for different strategies when faced with an unfamiliar context that we are really teaching mathematics in elementary school.

There are two different types of reasoning: inductive reasoning and deductive reasoning.

Inductive reasoning is also called bottom-up logic. When using inductive reasoning, people come to a conclusion based on observations. However, their conclusion may or may not be factual. For example, a student may observe that the following set of numbers is divisible by 4: 12, 36, 40, 48. They also notice that each of the numbers in the set are even. Therefore, they conclude that all even numbers are divisible by 4. This, however, is false.

Deductive reasoning is also called top-down logic and works the opposite way of inductive reasoning. When using deductive reasoning, people use known facts in order to reach a conclusion. For example, a student may be trying to determine if all even numbers are divisible by 4. They may use the examples 22 / 4 and 30 / 4 to prove that not all even numbers are divisible by 4. This makes deductive reasoning more reliable.

Why focus teaching and learning on reasoning?

Logical reasoning requires metacognition (thinking about thinking). It influences behavior and attitudes through greater engagement, requesting appropriate help (self-regulation) and seeking conceptual understanding.

Reasoning promotes these traits because it requires children to use their mathematical vocabulary. In short, reasoning requires a lot of active talk.

It is worth mentioning that with reasoning, active listening is equally important and if done right can also ensure increased learning autonomy for students.

The theory behind mathematical reasoning in elementary school

The infographic (below) from Helen Drury cleverly details what should underpin a mathematics teaching and learning syllabus. It’s a good starting point when you’re thinking about your mathematics curriculum in the context of fluency reasoning and problem solving.

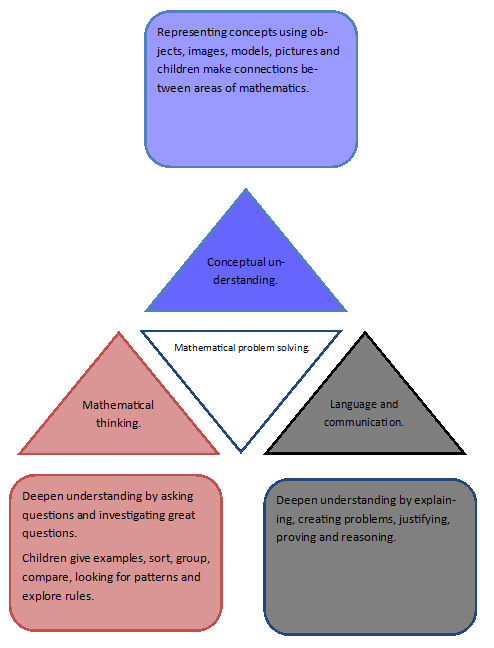
John bee reasoning and problem solving 1

I’ve also been very influenced by the Five Principles of Extraordinary Math Teaching by Dan Finkel

These are as follows, and are a great starting point to developing math reasoning at the elementary school level

1. Start math lessons with a question

2. Students need to wonder and struggle

3. You are not the answer key

4. Say yes to your students original ideas (but not yes to methodical answers)

5. Play!

How to make reasoning central to math lessons in elementary school

Pose lesson objectives as questions to elementary school children.

A ‘light bulb’ idea from my own teaching and learning was to redesign learning objectives, fashioning them into a question for learning. Instead of ‘to identify multiples of a number’, for example, I’ll use ‘why is a square number a square number?’. Another example is: instead of ‘to use ratio to describe the relationship between two quantities,’ we can ask students ‘in a recipe, if the ratio of sugar to flour is 3:5, what does that mean?’

Phrasing LOs as a question instantly engages and enthuses children, they wonder what the answer is. It also ensures that they show their reasoning in a model or image when they answer.

In this instance – interestingly – children knew the process to calculate square numbers but could not articulate or mathematically reason why it worked until after the session.

It seems denying children answers allows them time to use their thinking skills, struggle and learn.

Ban the word ‘yes’ in math lessons

One of the simplest strategies I have found to make reasoning inseparable from mathematical learning is to ban the word ‘yes’ from the classroom.

Instead, asking children to reason their thoughts and explain why they think they are right can allow for greater learning gains and depth of understanding. Admittedly, this is still a work in progress and easier said than done.

To facilitate this, I always tell my children that I am not the answer key.

Using my example of square numbers, I allowed children time to struggle and wrestle with my question without providing an answer or giving hints. Instead, I questioned the students to unpack understanding at the beginning of the lesson and brought together mathematical ideas during a whole class discussion.

After a short discussion on how children might show or visualize a square number we began to show a model using arrays, like below:

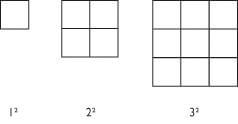
John bee reasoning and problem solving 2 1

The children working at greater depth were encouraged to consider cubed numbers and show how they might be represented using multi-link cubes without any input from me. This made sure links were made between math concepts, mathematical vocabulary, and learning.

Use ‘sometimes, always, never’ classroom activities

A ‘sometimes, always, never’ activity is another great way to foster reasoning and problem-solving skills. Take the image below:

John bee reasoning and problem solving 3 1

Here, children are first required to sort the fraction statements into always, sometimes or never being true. The next day, they are moved on to the lesson with the title phrased as a question. So not ‘to identify patterns’, but ‘how does this pattern work?’ with a pattern already presented on the board.

The children, instantly engaged, begin conjecturing, making predictions and thinking about the next patterns in the sequence (this lesson was actually inspired by an Nrich activity- a math education project run by the University of Cambridge).

5 tips for developing mathematical reasoning in the elementary school

While small changes will not provide the framework you need to properly embed reasoning in the classroom when implemented alongside ideas such as those mentioned above. These tips can help instill greater depth in math in your class for all ability levels.

1. Start lessons with a question.

2. Start lessons with a provocative mathematical statement or mind bender and challenge your class to provide the mathematical proof. Examples include:

“N will always = N”
“Multiples of 9 always have the digital sum of 9”.
“When multiplying decimals the number of decimals places in the answer will be the total number of decimal places in the two numbers being multiplied. (For example, the answer to 2.5 x 3.21, will have 3 decimal places.)”
“A square is always a rectangle, but a rectangle is not always a square.”

3. Present answers to exam questions as a puzzle to generate discussion and make connections. They can use their repertoire of math skills to explore the relationships between the numbers – does the line signify addition, subtraction, multiplication, etc. Puzzles could even be presented on a simple number line. When framed like this, children like to ‘come up’ with what the question could be:

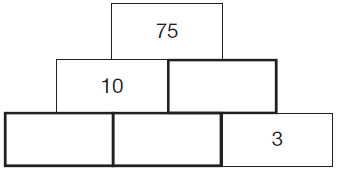
John bee reasoning and problem solving 4 1

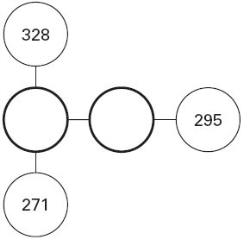
John bee reasoning and problem solving 5 1

4. Grouping children in threes is the magic number when working through problems. Child one talks through the problem. Child two writes down everybody’s reasoning. Child three actively listens and watches.

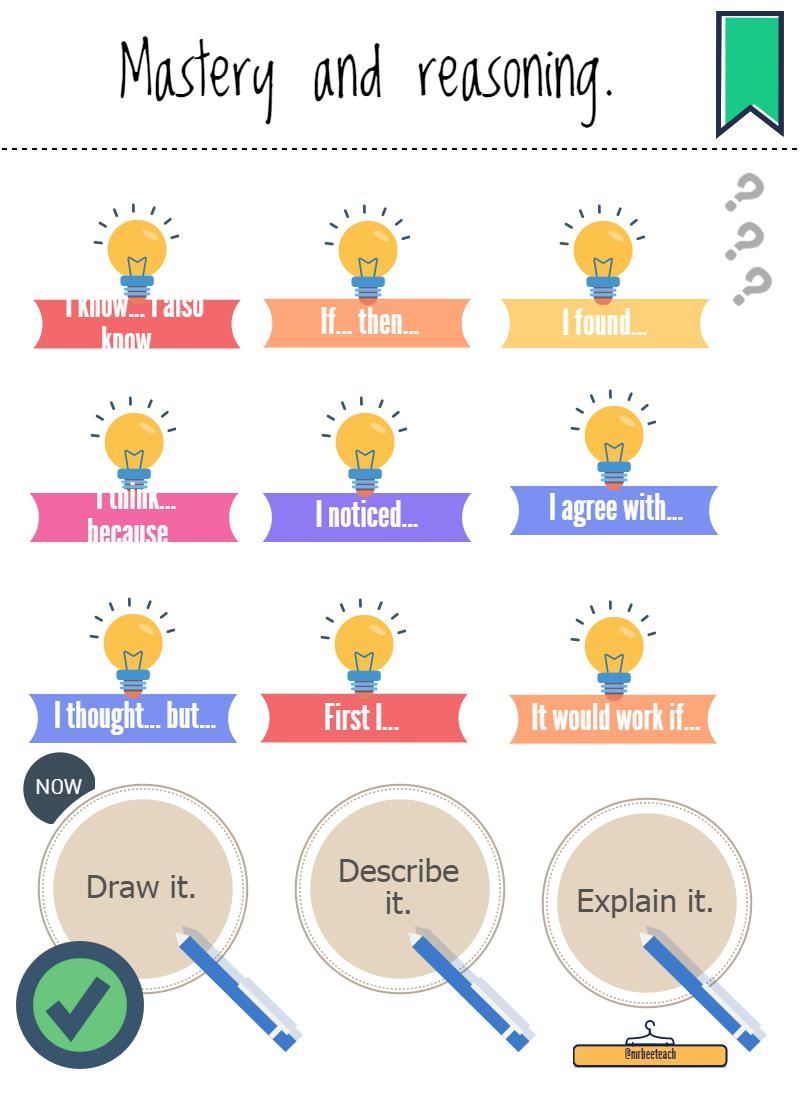
5. Include reasoning prompting posters around the classroom. The image below, for example, can be useful to children who are starting to formulate thoughts, predictions and assertions.

John Bee reasoning and problem solving 6

Your students will need an in-depth understanding of facts and concepts to truly succeed. Plus, they will need to be able to use and apply that knowledge to a range of contexts and in classroom discussion, in workbooks and in homework. As such, it’s clear that we need to provide them with a strong foundation of reasoning skills to give them their very best shot at the assessments they must face.