34 6th Grade Math Problems: Answers With Worked Examples
6th grade math problems signal a pivotal switch from concrete to abstract thinking in the math classroom. Teachers must act as facilitators to encourage critical thinking and problem solving skills, not just on the memorization of formulas.
In this article, we’ve listed 59 6th grade math problems to help students understand underlying principles and application of mathematics in real-world contexts. You can find all the math problems included in this article in a printable format in a convenient download.
What are 6th grade math problems?
6th grade math problems are math problems that suitably challenge 6th grade students to engage in abstract thinking. 6th grade is a pivotal year as students must switch from concrete to abstract thinking.
Students who have spent 5th grade and their early elementary years focusing on reasoning skills and utilizing math manipulatives to bring math alive tend to transition to fractions, graphing, and algebraic concepts such as pythagorean theorem practice problems more easily. Teaching students to identify patterns, draw pictures or models, and reason abstractly through problems teaches them to persevere and approach multi-step problems with ease.
Success in tackling 6th grade math problems depends on the following:
- Conceptual understanding of key concepts from the 6th grade math curriculum
- Effective teaching and support
- Elimination of math anxiety
- Practice in applying math and math formulas to a range of word problems
Math Games for 6th Graders
6 printable games for 6th graders that can be played in pairs, teams or as a whole class as a fun way to build math skills.
Download Free Now!6th grade math curriculum
There are five critical overarching math concepts in 6th grade:
- Ratios and Proportional relationships
- The Number System
- Expressions and Equations
- Geometry
- Statistics and Probability
While it is beneficial for students to learn traditional algorithms, it is even more crucial for them to develop flexible thinking, recognize patterns, and employ strategies to understand word problems and devise effective solutions.
To enhance mathematical comprehension and build perseverance in tackling multi-step problems, students must practice applying their mathematical skills in real-life contexts.
6th grade math curriculum: Common Core
Traditional mathematics teaching strategies emphasize formula memorization and specific learning patterns for each topic.
In contrast, Common Core aims to cultivate a deeper understanding by introducing broader foundational methods of thinking and strategies aligned with comprehensive learning approaches. When effectively integrated, Common Core math enhances critical thinking and fosters a deeper understanding of mathematical concepts, moving beyond the traditional focus on memorizing and applying formulas. The real-world application of mathematical concepts better prepares students for college and careers.

Meet Skye, the voice-based AI tutor making math success possible for every student.
Built by teachers and math experts, Skye uses the same pedagogy, curriculum and lesson structure as our traditional tutoring.
But, with more flexibility and a low cost, schools can scale online math tutoring to support every student who needs it.
Watch Skye in actionHow to teach 6th grade math problems
Drawing on my experience as a classroom teacher and the 10+ years of experience of Third Space Learning as one to one tutoring providers, here are some teaching strategies and ideas to enhance teaching and learning in your 6th grade math classroom:
1. I do, we do, you do
The I do, we do, you do approach allows teachers to model key skills and gradually release students to more independent practice. It offers a structured approach that enhances comprehension and retention of information. I do, we do, you do focuses students’ attention on essential information and provides a scaffolded resource that supports students as they tackle more complex, multi-step real-world problems.
In each of the 6th grade math problems included in this article, we’ve included step by step worked examples to support your classroom teaching.
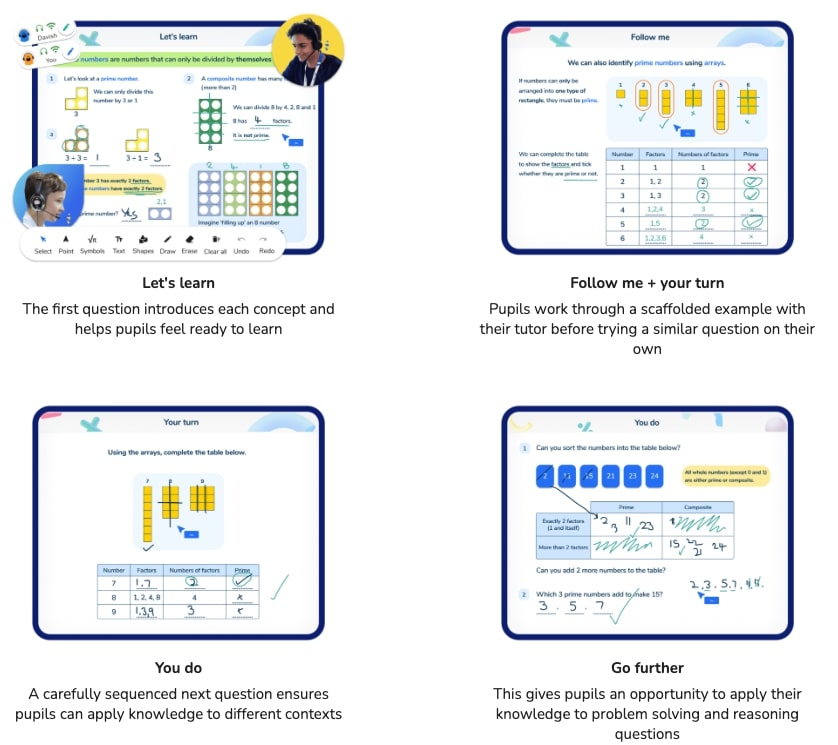
How can Third Space Learning help with math?
The I do, we do, you do method is central to the Third Space Learning math tutoring curriculum from K-8th grade. In Third Space Learning’s one to one online math tutoring sessions, tutors guide students through a problem using the interactive classroom.
The ‘Follow Me’ stage is where tutors break down new skills and concepts into manageable steps, providing verbal explanations and worked examples. Students complete a question with their tutor’s support, called ‘Your turn’. The worked example remains on the same screen for students to refer to as they work with their tutor to complete the new example. When students are ready, Third Space Learning tutors will gradually remove scaffolding to guide students to more independent practice. This stage is ‘You do’.
At every stage, scaffolding, support, and questioning allow tutors to fully personalize the learning experience to support all learners to progress.
2. Engage students in meaningful math talk
Math talk is crucial as it promotes deeper understanding, critical thinking, and collaboration among students. Effectively articulating mathematical ideas and reasoning enhances students’ ability to communicate complex concepts logically.
3. Collaborative problem-solving
Collaborative problem-solving boosts student confidence and motivation. It helps students to view themselves as capable mathematicians and reduces math anxiety. Math discourse supports academic growth and cultivates essential skills needed for future educational and career success.
For each math topic included in this article, there’s a project idea to promote this all-important collaboration.
34 6th grade math problems and solutions
In this article, you’ll find math problems and solutions for the following domains:
- Ratios and proportional relationships
- The number system
- Expressions and equations
- Geometry
- Statistics and probability
Under each domain, you’ll see:
- Practice exercises, guided notes and an answer key.
- Application problems designed to enhance students’ confidence and perseverance in solving word problems.
- Project idea designed to promote collaboration, suitable for use in-class, as homework projects or even as a math club activity.
Ratios and Proportional Relationships: 6th grade math problems
6th grade students work with:
- Integers
- Mixed numbers
- Rational numbers
- Complete operations with fractions
Solving these ratio word problems involves using greatest common factors (GCF), least common multiples (LCM), solving proportional relationships and common denominators.
Question 1
Determine if each pair of ratios forms a proportion:
a) \frac{4}{2} and \frac{30}{6}
b) \frac{3}{2} and \frac{18}{6}
c) \frac{4}{3} and \frac{20}{15}
d) \frac{6}{18} and \frac{1}{3}
Answer: a) no, b) no, c) yes, d) yes
Question 2
Solve each proportion:
a) \frac{x}{2} = \frac{30}{6}
b) \frac{15}{45} = \frac{2}{x}
c) \frac{12}{5} and \frac{x}{10}
d) \frac{7}{8} and \frac{56}{x}
Answer: a) x = 10, b) x = 6, d) x = 24, x = 64
Question 3
A recipe requires 2 cups of flour for every 3 cups of sugar. If you want to make a double batch of the recipe, how much flour do you need?
Answer: \frac{2 c flour}{3 c sugar} x \frac{2}{2} = \frac{4 c flour}{6 c sugar}
4 cups of flour
Question 4
A restaurant orders cans of black beans and cans of pinto beans. The ratio of the number of black beans to pinto beans is 2:3. What is the ratio of pinto beans to all beans?
a) 3:8
b) 3:5
c) 2:8
d) 2:5
Answer: Given: 2 black + 3 pinto = 5 total
2:3 = \frac{2 black}{3 pinto} and \frac{3 pinto}{5 all} = 3:5
Question 5
Samir bought gas for his car.
- Gas cost $3.45 per gallon.
- Samir bought 11.5 gallons.
What was the total cost for Samir’s gas?
Answer:
\frac{3.45 dollars}{1 gallon} = \frac{X dollars}{11.5 gallons}
\frac{3.45}{1 gallon} x \frac{11.5}{11.5} = \frac{39.675 dollars}{11.5 gallons}
He spent $39.68 on 11.5 gallons of gas
Question 6
Ed and Jim are debating the answer to the equation \frac{2}{3}m = \frac{1}{4}m .
- Jim states that m is equal to 2\frac{2}{3}.
- Ed states that m is equal to \frac{3}{8}.
Which statement is true?
a) Jim’s answer of 2\frac{2}{3} is correct because he divided \frac{2}{3} by \frac{1}{4} to get his answer.
b) Jim’s answer of 2\frac{2}{3} is correct because he divided \frac{1}{4} by \frac{2}{3} to get his answer.
c) Ed’s answer of \frac{3}{8} is correct because he multiplied \frac{1}{4} by \frac{2}{3} to get his answer.
d) Ed’s answer of \frac{3}{8} is correct because he divided \frac{1}{4} by \frac{2}{3} to get his answer.
Answer:
\frac{\ \frac{2}{3}m\ }{\frac{2}{3}} = \frac{\ \frac{1}{4}\ }{\frac{2}{3}}
m = \frac{1}{4} × \frac{3}{2}
m = \frac{3}{8}
Question 7
There are 4 cats for every 5 dogs in the pet store. How many cats and dogs could be in the pet store?
a) 64 cats and 80 dogs
b) 72 cats and 73 dog
c) 84 cats and 100 dogs
d) 96 cats and 110 dogs
Answer:
\frac{4}{5} x \frac{2}{2} = \frac{8}{10} x \frac{2}{2} = \frac{16}{20} x \frac{2}{2} = \frac{32}{40} x \frac{2}{2} = \frac{64}{80}
Question 8
a) (-2) + (-8)
b) (-3) – 7 + (-11)
c) -1000 ÷ 10³
Answer:
a) – 2 – 8 = – 10
b) -3 – 7 – 11 = – 21
c) – 1000 ÷ 1000 = – 1
Question 9
Add an inequality sign to show which number is greater.
a) (-6) ___ (-7)
b) -8 ___ 9
c) 67 ___ 84
d) -72 ___ -8
e) 3 ___ -14
Answer: a) > , b) < , c) < , d) < , e) >
Question 10
What is the value of M on the number line?

a) 5.5
b) 6
c) 7.5
d) 9
Answer: c) 7.5
Reasoning: Students need to estimate the value of each dash to determine the number represented on the number line. The number must fall between 5 and 10 which eliminates choice a and b; but 9, choice d, would be situated much closer to 10. The correct answer is c, 7.5.
Question 11
Which of the following numbers is greater than all the numbers in the list below?
-3.25, – \frac{7}{2} -3.1, -3\frac{3}{8}
a) -3.25
b) – \frac{7}{2}
c) -3.1
d) -3\frac{3}{8}
Answer: c) – 3.1
Reasoning: Understanding that negative numbers are greater when they are smaller due to them being closer to 0. Thus, -3.25 can be eliminated immediately because -3.1 is greater. Converting – \frac{7}{2} = -3.5 so it can be eliminated as it is less than -3.1. Last, compare -3\frac{3}{8} as a decimal is -3.333 which is also less than -3.1. Therefore, c, -3.1 is the correct answer.
Question 12
Which point shows the location of 43 on the number line?

a) Point M
b) Point N
c) Point R
d) Point T
Answer: b) Point N
Reasoning: Looking at the number line, students should recognize that each full point is broken into three sections. Thus, the individual lines can be counted as: 0, \frac{1}{3}, \frac{2}{3}, \frac{3}{3} = 1 , \frac{4}{3}, \frac{5}{3}… Therefore, R is \frac{4}{3}.
Question 13
Which list of numbers is ordered from greatest to least?
a) 1.5, \frac{2}{3}, – \frac{3}{4}, – 1.2
b) 1.5, -1.2, \frac{2}{3}, – \frac{3}{4}
c) \frac{2}{3}, 1.5, -1.2, – \frac{3}{4}
d) \frac{2}{3}, 1.5, – \frac{3}{4}, -1.2
Answer: a) 1.5, \frac{2}{3}, – \frac{3}{4}, – 1.2
Reasoning: Logically, negative numbers are smaller than positive numbers, thus, option b can be eliminated immediately. Understanding that when the numerator is smaller than the denominator you have a decimal less than one whole, students can eliminate option c and d as \frac{2}{3} < 1.5. The correct answer is a.
Question 14
Sarah was hiking in the mountains. She started her hike at an elevation of 800 meters above sea level. She climbed up 250 meters to reach a peak and then descended 450 meters to a valley. What is her elevation at the valley?
Answer: 800 + 250 – 450 = 600
Sarah is 600 meters above sea level.
Expressions and equations: 6th grade math problems
6th grade students must utilize their skills in working with order of operations and rational numbers to write equations from word problems and solve one-step and two-step equations. The solving of word problems involves working with fractions, divisors, integers, and percents in multi-step situations to determine the final value.
Question 15
Evaluate the expression:
a) (5² -10) ÷ 5 x 2³
b) -3 x = 48
c) \frac{1}{3}x = 9\frac{1}{3}
Answer:
a)
= (25-10) ÷ 5 x 8
= (15) ÷ 5 x 8
= 3 x 8
= 24
b)
\frac{-3x}{-3} = \frac{48}{-3}
x = – 16
c)
\frac{1}{3}x = 9\frac{1}{3}
\frac{1}{3}x = \frac{28}{3}
\frac{\ \frac{1}{3}x\ }{\frac{1}{3}} = \frac{\ \frac{28}{3}\ }{\frac{1}{3}}
x = \frac{28}{3} × \frac{3}{1}
x = 28Question 16
Sebastian pays $250 each month to rent an office where she earns $35 per hour tutoring students. Which equation represents Sebastian’s profit, y , for working x hours?
a) y = 35 + 250 x
b) y = 35 x + 250
c) y = 35 – 300 x
d) y = 35 x -250
Answer: d) y = 35 x – 250
Reasoning: The starting amount he must pay is $250. The “per hour” implies multiplication as “per” means “to multiply.” Thus, the x must be multiplied by 35. Lastly, understanding that profit is determined by subtracting away expenses from any income forces the elimination of choices a and b. The correct answer is d, y = 35 x -300.
Question 17
Kedar runs the same number of miles, x , every week. His total distance run over the week is less than 60 miles. Which inequality represents how many miles Kedar runs each week?
a) x ≥ 60
b) x ≤ 60
c) x ≻ 60
d) x ≺ 60
Answer: d) x ≺ 60
Reasoning: The original problem states “less than 60” so students should recognize the need to plug in a number for the variable x to ensure the possible answer makes logical sense. Use 50, which is less than 60, and you can eliminate choice a and b. The determining factor is the number 60. Is “60 less than 60” or is “60 less than or equal to 60”. The problem wanted “less than,” thus, the correct answer is d.
Question 18
What is the value of (5 p + \frac{1}{4} )² when p = 0?
Answer:
(5 p + \frac{1}{4} )²
(5(0) + \frac{1}{4} )²
(\frac{1}{4} )²
\frac{1}{16}Question 19
During a weekend special event, the manager of a bookstore gave away gift cards to every 75th person who visited the mall.
- On Saturday, 2,100 people visited the mall.
- On Sunday, 1,675 people visited the mall.
How many people received gift cards?
Answer: The manager gave away 50 gift cards.
Reasoning: To determine how many gift cards are given away, the student must recognize that the problem involves the need to divide the total number of people into groups of 75.
\frac{total people}{75} = number of gift cards given away
\frac{2100 + 1675}{75}\frac{3775}{75} = 50.33
The manager gave away 50 gift cards.
Question 20
Maria is saving money to buy a new bicycle. She has already saved $45. Each week, she earns $15 from her allowance and an additional $10 from doing extra chores. She plans to save all of this money every week. How many weeks will it take for Maria to have at least $300 saved.
Answer:
Step 1: Calculate how much Maria saves each week.15+10=25 dollars per week
Step 2: Set up an expression for the total amount saved after w weeks:
45+25 w
Step 3: Determine the number of weeks required for Maria to have at least $300 saved:
45 + 25 w ≥ 300
Step 4: Solve inequality:
45 + 25 w ≥ 300
-45 -45
25 w ≥ 255
\frac{25w}{25} ≥ \frac{255}{25}
w ≥ 10.2
Since Maria can’t save for a fraction of a week, she will need to save for at least 11 weeks to have at least $300.
Geometry: 6th grade math problems
6th grade geometry deals with using formulas, two-dimensional, and three-dimensional shapes, including parallelograms and quadrilaterals. Students must pay attention to customary units (metric, imperial, etc.) and use substitution and solving equations in addition to memorizing formulas.
Question 21
What is the area of the triangle rounded to the nearest hundredth?
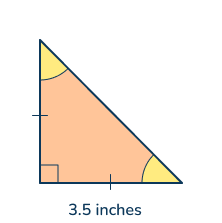
Answer:
A = \frac{1}{2}bh
A = \frac{3.5 × 3.5}{2}
A = \frac{12.25}{2}bh
A = 6.125
A = 6.13 in²
Question 22
The graph shows segment AB and Point C
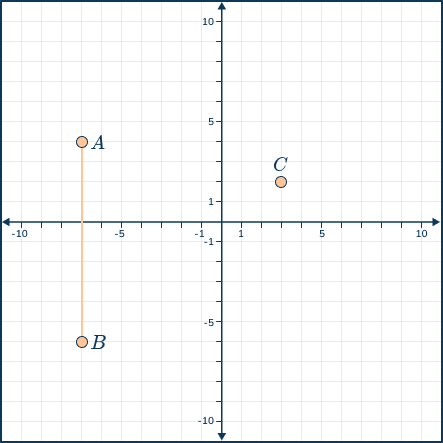
- Point M is located in the fourth quadrant.
- The distance between point C and point M is half the distance between point A and point B.
- Segment CM is parallel to segment AB.
What is the ordered pair of point M?
a) (7, 2)
b) (2, 7)
c) (-3, 2)
d) (3, -3)
Answer: d) (3, -3)
Reasoning: Quadrant four is the lower right-hand quadrant without any existing points. Thus, the student would count line segment AB and determine the length is 10 units. Since half of 10 is 5, the student would count 5 units down from point C to point (2, -3)
Question 23
Suzy is wrapping a cube-shaped box and wants to make sure she has enough wrapping paper. The net for the box is shown.
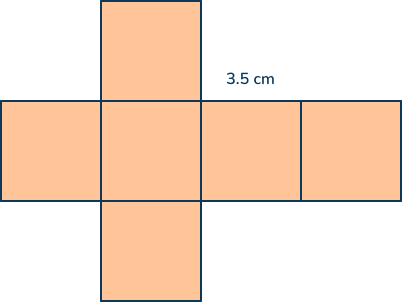
What is the area she needs to cover?
a) 73.5 cm²
b) 21 cm²
c) 42 cm²
d) 96.25 cm²
Answer: a) 3.5cm x 3.5cm x 6 = 73.5cm²
Reasoning: Students need to remember that surface area can be solved by adding the area of each shape. Since this is a cube, there are six identical sides. Area of a square is solved by multiplying length times width. Then, multiply that area times 6.
Question 24
How much water can Sier hold in his fish tank if it has a length of 4 feet, a width of 3 feet, and a height of 5 feet?
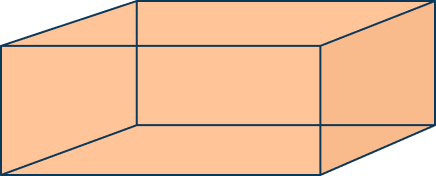
Answer: V = 60 feet³
Reasoning: Students should recognize this as a rectangular prism and now that volume is the term related to how much something can hold. Therefore, the correct answer is:
V = L × W × H =
V = 4 feet × 3 feet × 5 feet
V = 60 feet³
Question 25
Calculate the length of the hypotenuse of a right triangle with legs measuring 6 cm and 8 cm.
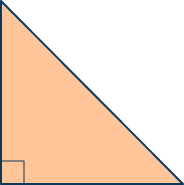
Answer: 10 cm
Reasoning: Students will remember that the hypotenuse is the side opposite of the right angle and c in the pythagorean theorem. Thus, 6 and 8 are the sides that form the right angle and used for variables a and b . Then, students will use the pythagorean theorem to solve for the hypotenuse.
a² + b² = c²(6)² + (8)² = c²
36 + 64 = c²
100 = c²
\sqrt{100} = c²
10 = c
Question 26
Emma and John are playing a treasure hunt game on a coordinate plane. Emma’s starting point is at (2,3) and John’s starting point is at (8, -2). They both move to the treasure located at (8,7).
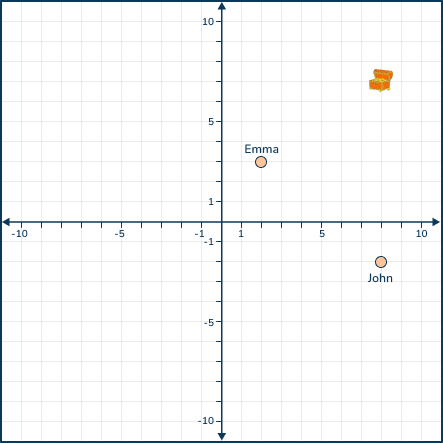
a) Calculate the distance Emma travels to reach the treasure.
b) Calculate the distance John travels to reach the treasure.
c) Determine who travels the longer distance.
Answer:
a) Calculate Emma’s distance using the pythagorean theorem by first creating a right triangle where the 90° angle would be at (8,3); therefore 6 units right and 4 units up to the treasure.
a²+b² = c²
(6)²+(4)² = c²
36 + 16 = c²
52 = c²
\sqrt {52} = \sqrt {c²}7.21 ≈ c
b) Calculate John’s distance to the treasure. Because it is a straight line, students can determine he is 9 units from the treasure.
c) John will travel further.
Statistics and probability: 6th grade math problems
Question 27
If the probability of picking a red marble from a bag is \frac{1}{4} , what is the probability of not picking a red marble?
a) \frac{1}{2}
b) \frac{1}{4}
c) \frac{3}{4}
d) \frac{1}{3}
Answer: c) \frac{3}{4}
Reasoning: The odds of an event occurring and the odds of the event not occurring must add up to 100% or 1 whole. Thus, if picking a red marble is \frac{1}{4} , then you subtract \frac{1}{4} from 1 to determine the probability of the event not occurring.
not occuring + occurring = 1
x + \frac{1}{4} = 1
– \frac{1}{4} – \frac{1}{4}
x = \frac{4}{4} – \frac{1}{4}
x = \frac{3}{4}
Question 28
The following data set represents the number of books read by students in a class over a one month period of time: 3, 5, 8, 3, 6, 7, 3, 9, 5, 4.
a) Find the range.
b) Find the mean.
c) Find the median.
d) Find the mode.
Answer:
a) Mean = 5.3
Reasoning: Mean is the average of the numbers. Add them all and divide by 10 because there are 10 numbers in the set.
\frac{3 + 5 + 8 + 3 + 6 + 7 + 3 + 9 + 5 + 4}{10} = \frac{53}{10} = 5.3
b) Median = 5
Reasoning: Ordered data = 3, 3, 3, 4, 5, 5, 6, 7, 8, 9.
The middle two numbers are 5 and 5. Thus, take the average: \frac{5 + 5}{2} = \frac{10}{2} = 5
c) Mode = 3
Reasoning: This is the number that repeats most often.
d) Range = 6
Reasoning: Subtract the lowest number from the highest to determine range: 9 – 3 = 6
Question 29
The table below shows the number of hours students spend on homework per week:
| Hours | Frequency |
| 0 – 2 | 4 |
| 3 – 5 | 6 |
| 6 – 8 | 8 |
| 9 – 11 | 2 |
a) What is the total number of students surveyed?
b) What is the most common range of hours spent on homework?
Answer:
a) Total number of students: 4 + 6 + 8 + 2 = 20
b) Most common range (mode): 6 – 8 hours
Question 30
A jar contains 10 red, 15 blue, and 5 green marbles. If one marble is selected at random:
a) What is the probability of selecting a blue marble?
b) What is the probability of selecting a red or green marble?
Answer:
a) Probability of selecting a blue marble = \frac{blue}{total no. marbles} = \frac{15}{10+15+5} = \frac{15}{30} = \frac{1}{2}
b) Probability of selecting a red or green marble = \frac{red + green}{total no. marbles} = \frac{15}{30} = \frac{1}{2}
Question 31
The following numbers represent the scores of 10 students on a math test: 45, 67, 72, 78, 81, 85, 88, 90, 92, 95.
Fill in the box and whisker plot labeling the median, lower quartile (Q1), upper quartile (Q3), the minimum and maximum numbers and enter their values.
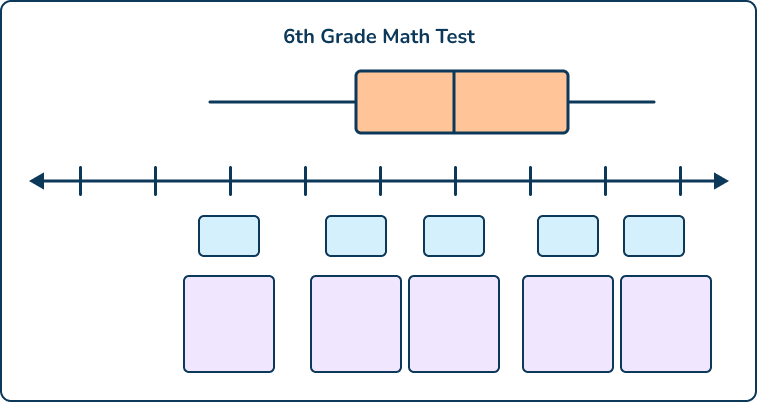
Answer:
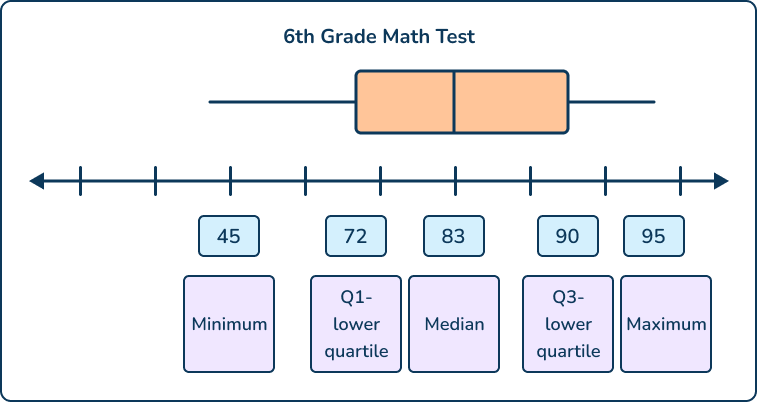
Reasoning:
Step 1: Order the numbers from low to high. 45, 67, 72, 78, 81, 85, 88, 90, 92, 95
Step 2: Determine the location of the following words: minimum, lower quartile, median, upper quartile, maximum.
Step 3: Determine the minimum and maximum values and place in the first and last blue box.
Step 4: Solve for the median by determining the number in the middle = 83
Step 5: Solve for the median of the lower half of the data set (lower quartile) by listing the first half of the numbers from low to high: 45, 67, 72, 78, 81. The median is 72 (the number in the middle).
Step 6: Solve for the median of the upper half of the data set (upper quartile) by listing the second half of the numbers from low to high: 85, 88, 90, 92, 95. The median is 90 (the number in the middle).
Question 32
Rosa is going to survey her classmates to find out if more students walk to school or ride the bus to school. Which sample method is biased?
a) Surveying 25 students chosen randomly on the bus
b) Surveying 25 students chosen randomly in the library
c) Surveying 25 students chosen randomly in the cafeteria
d) Surveying 25 students chosen randomly at an assembly
Answer: a) Surveying 25 students chosen randomly on the bus
Reasoning: Bias should be avoided in statistical analysis and surveys. Participants should be selected randomly, but from a location not involved in your survey.
Question 33
Which of the following describes independent events?
a) Choose a set of earrings, put them on, then choose another set of earrings.
b) Draw a marble from a bag. Do not replace it. Draw another marble.
c) Pick a vegetable for a side dish, then pick a meat for a main course.
d) Pick a name from a hat. Do not replace it. Pick another name.
Answer: c) Pick a vegetable for a side dish, then pick a meat for a main course.
Reasoning: Independent events are events that do not depend on any other event. Solutions a, b, and d all alter the probability because the number of items to choose from is decreased when the first item picked is not returned to the set. However, option c, the number of vegetables is unlimited as is the type of meat. The meat and vegetables do not depend on each other or alter the number of choices.
6th grade math worksheets
Looking for more math worksheets and resources? See our 6th grade math test and selection of sixth grade math worksheets covering key 6th grade topics and more:
- Distributing Exponents Worksheet
- Dividing Decimals Worksheet
- One step equations Worksheet
- Ratio Problem Solving Worksheet
- Fraction to Decimal Worksheet
- Adding and Subtracting Integers Worksheet
- Exponential Notation Worksheet
- 9 Algebra Questions for Middle School
- Greatest Common Factor Worksheet
- Least Common Multiple Worksheet
Frequently asked questions
What do 6th graders struggle with in math?
6th grade math can feel challenging for students. The biggest challenge is the switch to abstract thinking. Learning to identify patterns, draw pictures or models, and reason abstractly through problems will help students to persevere and tackle 6th grade multi-step problems with ease.
What should a 6th grader know in math?
There are five critical overarching math concepts in 6th grade: ratios and proportional relationships, the number system, expressions and equations, geometry statistics, and probability. 6th graders need to know not only the content of these topics, but also know how to use their knowledge and apply their reasoning skills to a range of math problems.
How hard is math for 6th graders?
6th grade math can feel challenging for students. Sixth grade is when you begin building the foundations of algebra, geometry, and statistics. It also marks a switch from concrete to abstract thinking. However, with the right support and opportunity to practice, all students can succeed in 6th grade math.
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Why not learn more about how it works?
Meet Skye, our AI voice tutor. Built on over a decade of tutoring expertise, Skye uses the same proven pedagogy and curriculum as our traditional tutoring to close learning gaps and accelerate progress. Watch a clip of Skye’s AI math tutoring in action.







