25 Fun Math Problems For Elementary And Middle School (From Easy To Very Hard!)

Fun math problems and brainteasers are loved by mathematicians; they provide an opportunity to apply mathematical knowledge, logic, and problem-solving skills all at once.

In this article, we’ve compiled 25 fun math problems and brainteasers covering various topics and question types. They’re aimed at students in upper elementary (3rd-5th grade) and middle school (6th grade, 7th grade, and 8th grade). We’ve categorized them as:

How should teachers use these math problems?

Teachers could make use of these math problem solving questions in a number of ways. They can:

• incorporate the questions into a relevant math lesson.
• set tasks at the beginning of lessons.
• break up or extend a math worksheet.
• keep students thinking mathematically after the main lesson has finished.

Some are based on real life or historical math problems, and some include ‘bonus’ math questions to help extend the problem-solving fun! As you read through these problems, think about how you could adjust them to be relevant to your students and their grade level or to practice different math skills. 

These math problems can also be used as introductory puzzles for math games such as those introduced at the following links:

• Math games for grade 4
• Middle school math games

Math word problems

1. Home on time – easy 

Type: Elapsed time, Number, Addition

A movie theater screening starts at 2:35 pm. The movie lasts for 2 hours, 32 minutes after 23 minutes of previews. It takes 20 minutes to get home from the movie theater. What time should you tell your family that you’ll be home?

Answer: 5:50 pm

2. A nugget of truth – mixed

Type: Multiplication Facts, Multiplication, Multiples, Factors, Problem-Solving 

Chicken nuggets come in boxes of 6, 9 or 20, so you can’t order 7 chicken nuggets. How many other impossible quantities can you find (not including fractions or decimals)?

Answer: 1, 2, 3, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 22, 23, 25, 28, 31, 34, 37, or 43

There is actually a theorem which can be used to prove that every integer quantity greater than 43 can be ordered.

3. A pet problem – mixed

Type: Number, Problem Solving, Forming and Solving Equations, Simultaneous Equations, Algebra

Eight of my pets aren’t dogs, five aren’t rabbits, and seven aren’t cats. How many pets do I have?

Answer: 10 pets (5 rabbits, 3 cats, 2 dogs)

Looking for more word problems, solutions and explanations? Read our article on word problems for elementary school.

4. The price of things – mixed

Type: lateral thinking problem

A mouse costs $10, a bee costs $15, and a spider costs $20. Based on this, how much does a duck cost?

Answer: $5 ($2.50 per leg)

Math puzzles

5. A dicey math challenge – easy

Type: Place value, number, addition, problem-solving

Roll three 6 sided dice to generate three place value digits. What’s the biggest number you can make out of these digits? What’s the smallest number you can make?

Add these two numbers together. What do you get?

Answer: If the digits are the same, the maximum is 666 and the minimum is 111.
Then, if you add the numbers together, 666 + 111 = 777.

If the digits are different, the maximum is 654 and the minimum is 456.
Then, if you add the numbers together, 654 + 456 = 1,110.

Bonus: Who got a different result? Why?

6. PIN problem solving – mixed

Type: Logic, problem solving, reasoning

I’ve forgotten my PIN. Six incorrect attempts locks my account: I’ve used five! Two digits are displayed after each unsuccessful attempt: “2, 0” means 2 digits from that guess are in the PIN, but 0 are in the right place. No two digits in my PIN are the same.

What should my sixth attempt be?

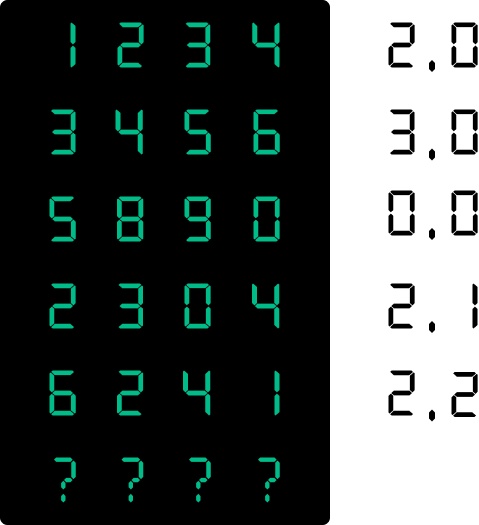
Answer: 6347

7. So many birds – mixed

Type: Triangular Numbers, Sequences, Number, Problem Solving

On the first day of Christmas my true love gave me one gift. On the second day they gave me another pair of gifts plus a copy of what they gave me on day one. On day 3, they gave me three new gifts, plus another copy of everything they’d already given me. If they keep this up, how many gifts will I have after twelve days?

Answer: 364

Bonus: This could be calculated as 1 + (1 + 2) + (1 + 2 + 3) + … but is there an easier way? What percentage of my gifts do I receive on each day?

8. I 8 sum math questions – mixed

Type: Number, Place Value, Addition, Problem Solving, Reasoning

Using only addition and the digit 8, can you make 1,000? You can put 8s together to make 88, for example.

Answer: 888 + 88 + 8 + 8 + 8 = 1,000

Bonus: Which other digits allow you to get 1,000 in this way?

---

Fraction problems

4 friends entered a math quiz. One answered \frac {1}{5} of the math questions, one answered \frac {1}{10} , one answered \frac{1}{4} , and the other answered \frac{4}{25} . What percentage of the questions did they answer altogether?

Answer: 71%

10. Ancient problem solving – easy

Type: Fractions, Reasoning, Problem Solving

Ancient Egyptians only used unit fractions (like \frac {1}{2} , \frac{1}{3} or \frac{1}{4} . For \frac {2}{3} they’d write \frac{1}{3} + \frac{1}{3} . How might they write \frac{5}{8} ?

Answer: 

\frac {1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} is correct. So is \frac {1}{2} + \frac{1}{8} (They are both still unit fractions even though they have different denominators.)

Bonus: Which solution is better? Why? Can you find any more? What if subtractions are allowed?

Learn more about unit fractions here.

11. Everybody wants a pizza the action – hard

Type: Fractions, Reasoning, Problem Solving

An infinite number of mathematicians buy pizza. The first wants \frac{1}{2} . The second wants \frac{1}{4} pizza. The third & fourth want \frac{1}{8} and \frac{1}{16} each, and so on. How many pizzas should they order?

Answer: 1
Each successive mathematician wants a slice that is exactly half of what is left:

12. Shade it black – hard

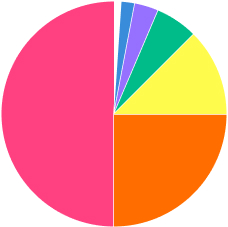
Type: Fractions, Reasoning, Problem Solving
What fraction of this image is shaded black?

Answer: 

\frac{1}{3}

Look at the L-shaped part made up of two white and one black squares: 

\frac{1}{3} of this part is shaded. Zoom in on the top-right quarter of the image, which looks exactly the same as the whole image, and use the same reasoning to find what fraction of its L-shaped portion is shaded. Imagine zooming in to do the same thing again and again…

---

Multiplication and division problems

13. Giving is receiving – easy

Type: Number, Reasoning, Problem Solving

5 people give each other a present. How many presents are given altogether?

Answer: 20

14. Sharing is caring – mixed

Type: Number, Reasoning, Problem Solving

I have 20 candies. If I share them equally with my friends, there are 2 left over. If one more person joins us, there are 6 candies left. How many friends am I with?

Answer: 6 people altogether (so 5 friends!)

15. Multiplication facts secrets – mixed

Type: Area, 2D Shape, Rectangles

Here are 77 letters:

B Y H R C G N E O E A A H G C U R P U T S A S H H S B O R E O P E E M E E L A T P E F A D P H L TU T I E E O H L E N R Y T I I A G B M T N F C G E I I G

How many different rectangular grids could you arrange all 77 letters into?

Can you reveal the secret message?

Answer: Four: 1 × 77, 77 × 1, 11 × 7 and 7 × 11. If the letters are arranged into one of these, a message appears, reading down each column starting from the top left.

Bonus: Can you find any more integers with the same number of factors as 77? What do you notice about these factors (think about prime numbers)? Can you use this system to hide your own messages?

16. Laugh it up – hard

Type: Multiples, Least Common Multiple, Multiplication Facts, Division, Time

One friend jumps every \frac{1}{3} of a minute. Another jumps every 31 seconds. When will they jump together?

Answer: After 620 seconds

---

Geometry problems

17. Pictures of matchstick triangles – easy

Type: 2D Shapes, Equilateral Triangles, Problem Solving, Reasoning

Look at the matchsticks arranged below. How many equilateral triangles are there?

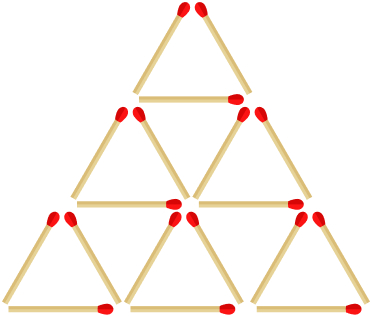
Answer: 13 (9 small, 3 medium, 1 large)

Bonus: What if the biggest triangle only had two matchsticks on each side? What if it had four?

18. Dissecting squares – mixed

Type: Reasoning, Problem Solving

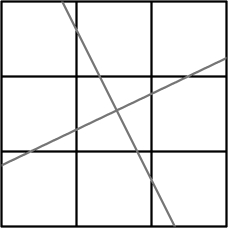
What’s the smallest number of straight lines you could draw on this grid such that each square has a line going through it?

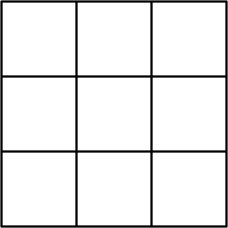
Answer: 2

e.g.

19. Make it right – mixed

Type: Pythagorean theorem

This triangle does not agree with Pythagorean theorem. 

Adding, subtracting, multiplying or dividing each of the side lengths by the same whole number can fix it. What is the number?

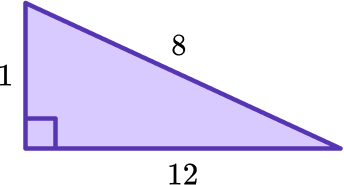
Answer: 3 

3 × 1 = 3

8 – 3 = 5

12 ÷ 3 = 4

The new side lengths are 3, 4 and 5 and  32 + 42 = 52.

20. A most regular math question – hard

Type: Polygons, 2D Shapes, tessellation, reasoning, problem-solving, patterns

What is the regular polygon with the largest number of sides that will self-tessellate?

Answer: Hexagon.

Regular polygons tessellate if one interior angle is a factor of 360°. The interior angle of a hexagon is 120°. This is the largest factor less than 180°.

---

Problem-solving questions

21. Pleased to meet you – easy

Type: Number Problem, Reasoning, Problem Solving

5 people meet; each shakes everyone else’s hand once. How many handshakes take place?

Answer: 10

Person A shakes 4 people’s hands. Person B has already shaken Person A’s hand, so only needs to shake 3 more, and so on.

Bonus: How many handshakes would there be if you did this with your class?

22. All relative – easy

Type: Number, Reasoning, Problem-Solving

When I was twelve my brother was half my age. I’m 40 now, so how old is he?

Answer: 34

23. It’s about time – mixed

Type: Time, Reasoning, Problem-Solving

When is “8 + 10 = 6” true?

Answer: When you’re telling the time (8am + 10 hours = 6pm)

24. More than a match – mixed

Type: Reasoning, Problem-Solving, Roman Numerals, Numerical Notation

Here are three matches:

How can you add two more matches, but get eight?

Answer: Put the extra two matches in a V shape to make 8 in Roman Numerals:

25. Leonhard’s graph – hard

Type: Reasoning, Problem-Solving, Logic

Leonhard’s town has seven bridges as shown below. Can you find a route around the town that crosses every bridge exactly once?

Answer: No!

This is a classic real life historical math problem solved by mathematician Leonhard Euler (rhymes with “boiler”). The city was Konigsberg in Prussia (now Kaliningrad, Russia). Not being able to find a solution is different from proving that there aren’t any! Euler managed to do this in 1736, practically inventing graph theory in the process.

Math puzzles are everywhere!

Many of these 25 math problems are rooted in real life, from everyday occurrences to historical events. Others are just questions that might arise if you say “what if…?”. The point is that although there are many lists of such problem-solving math questions that you can make use of, with a little bit of experience and inspiration you could create your own on almost any topic – and so could your students. 

For a kick-starter on creating your own math problems, read our article on middle school math problem solving.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by primary school teacher Tom Briggs and has since been revised and adapted for US schools by math curriculum specialist and former elementary math teacher Katie Keeton.