Decimal place value

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

Place value Arithmetic BIDMAS

This topic is relevant for:

GCSE Maths Number FDP Decimals

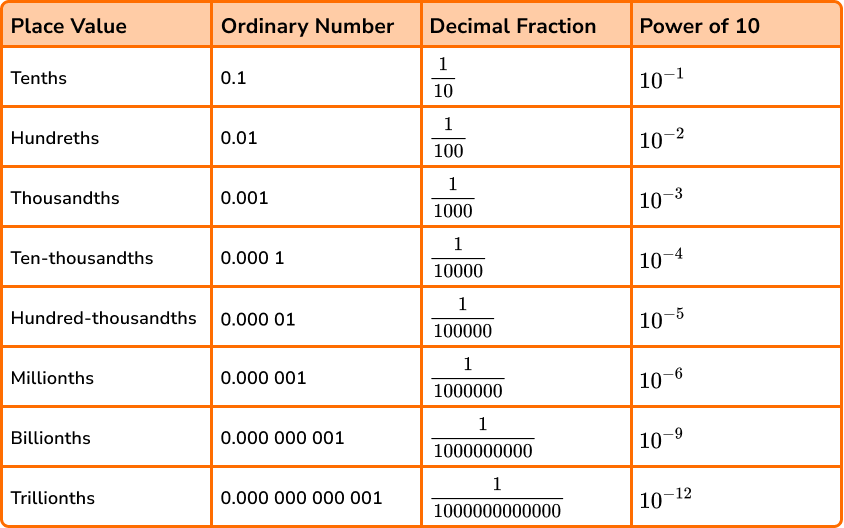
Decimal Place Value

Here we will learn about decimal place values, including what place value means for decimal numbers and how to use it.

There are also decimal place value worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is decimal place value?

Decimal place value extends our understanding of place value to decimal numbers. Decimal places are the digits to the right of the decimal point.

The place value of a number helps us to understand the value of each digit in the number. To determine the value of each digit in a number we can use a place value chart or place value grid.

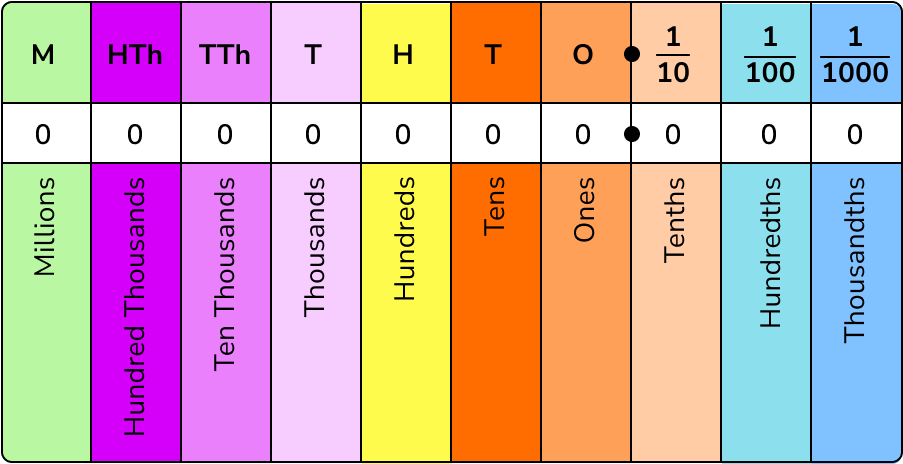
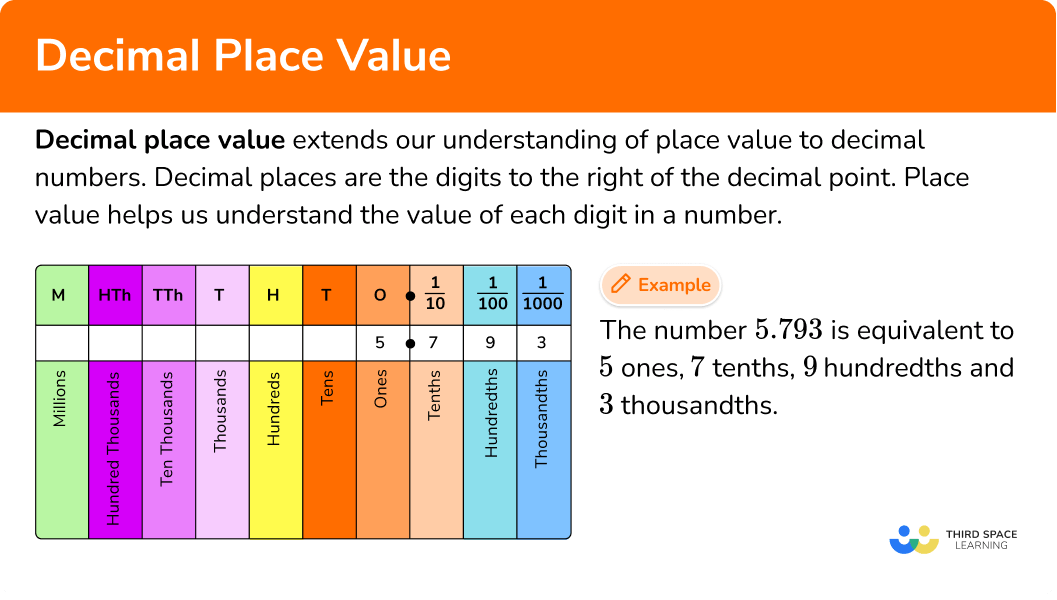
For example, let’s place the number $5.793$ into the place value chart.

The digit $5$ goes in the ones column.

The digit $7$ goes in the tenths column.

The digit $9$ goes in the hundredths column.

The digit $3$ goes in the thousandths column.

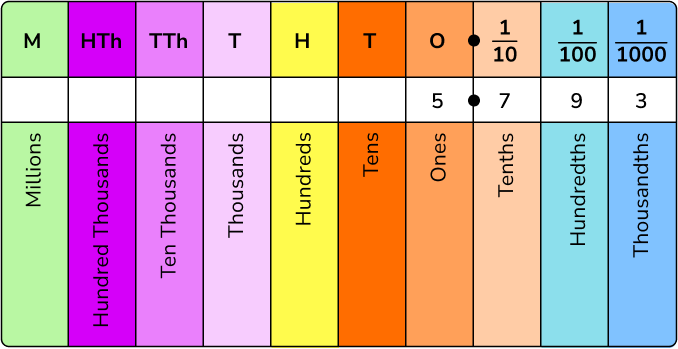
This means that the number $5.793$ is equivalent to $5$ ones, $7$ tenths, $9$ hundredths and $3$ thousandths.

What is decimal place value?

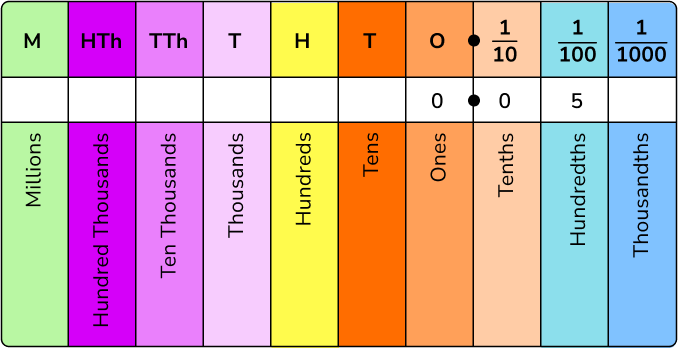
Zero place holder

Sometimes we need to use zero as a placeholder in decimal numbers.

For example, the number $0.05$ has zeros in the ones column and the tenths column. To indicate there are no ones and no tenths.

Decimal fractions

Decimal fractions are fractions where the denominator is $10, \ 100, \ 1000$ or another power of $10.$

For example,

\frac{3}{10} \hspace{1cm} \frac{17}{100} \hspace{1cm} \frac{376}{1000} \hspace{1cm} \frac{19}{1000000}

Decimal fractions can also be used to write the value of the digits in a decimal number. This means that in the number $5.793$ the digit $9$ is worth $9$ hundredths or $0.09$ or $\frac{9}{100}.$

Very small numbers

Decimal place values can be extended beyond tenths, hundredths and thousandths.

The decimal place value chart could be extended so there are more columns to the right. Powers of ten can be used to help write very small numbers.

Ordering decimals

Decimal place value can help with ordering decimals.

For example,

Place these decimals in size order from smallest to largest.

0.06 \hspace{1cm} 0.1 \hspace{1cm} 0.007 \hspace{1cm} 0.0009

Let’s take each decimal and compare the place value of the digits.

The digit $9$ in $0.0009$ represents $9$ ten-thousandths. This is the smallest value.

The digit $7$ in $0.007$ represents $7$ thousandths. This is the next biggest value.

The digit $6$ in $0.06$ represents $6$ hundreths. This is the next biggest value.

The digit $1$ in $0.1$ represents $1$ tenth. This is the biggest value.

The decimals in order of size from smallest to largest will be:

0.0009 \hspace{1cm} 0.007 \hspace{1cm} 0.06 \hspace{1cm} 0.1

How to write the value of a digit in a decimal number

In order to write the value of a digit in a decimal number:

Locate the digit within the number.
Recall the place value of that column.
Write the value of the digit.

Explain how to write the value of a digit in a decimal number

[FREE] Decimals Worksheet (GCSE)

Get your free decimals worksheet with 44 questions and answers to help your students prepare for their Maths GCSE. This resource includes reasoning and applied questions.

FREE DOWNLOAD

[FREE] Decimals Worksheet (GCSE)

Get your free decimals worksheet with 44 questions and answers to help your students prepare for their Maths GCSE. This resource includes reasoning and applied questions.

FREE DOWNLOAD

Related lessons on decimals

Decimal place value is part of our series of lessons to support revision on decimals. You may find it helpful to start with the main decimals lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Decimal place value examples

Example 1: tenths

Write the value of $3$ in the number $4.392.$

Locate the digit within the number.

2Recall the place value of that column.

The $3$ is in the tenths place.

3Write the value of the digit.

The digit and the place value of the digit combine to give the value of the digit.

The value of the digit $3$ in the number $4.392$ is $3$ tenths or $0.3$ or as a decimal fraction $\frac{3}{10}.$

Example 2: tenths

Write the value of $7$ in the number $5.708.$

Locate the digit within the number.

Recall the place value of that column.

The $7$ is in the tenths column.

Write the value of the digit.

The digit and the place value of the digit combine to give the value of the digit.

Note: The $0$ in the hundredths column is a placeholder.

The value of the digit $7$ in the number $5.708$ is $7$ tenths or $0.7$ or as a decimal fraction $\frac{7}{10}.$

Example 3: hundredths

Write the value of $8$ in the number $6.489.$

Locate the digit within the number.

Recall the place value of that column.

The $8$ is in the hundredths column.

Write the value of the digit.

The digit and the place value of the digit combine to give the value of the digit.

The value of the digit $8$ in the number $6.489$ is $8$ hundredths or $0.08$ or as a decimal fraction $\frac{8}{100}.$

Example 4: hundredths

Write the value of $2$ in the number $30.1289.$

Locate the digit within the number.

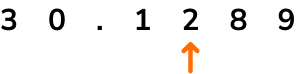
Recall the place value of that column.

The $2$ is in the hundredths place.

Write the value of the digit.

The digit and the place value of the digit combine to give the value of the digit.

Note: The $0$ in the ones column is a placeholder.

The value of the digit $2$ in the number $30.1289$ is $2$ hundredths or $0.02$ or as a decimal fraction $\frac{2}{100}.$

Example 5: thousandths

Write the value of $1$ in the number $35.941.$

Locate the digit within the number.

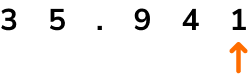
Recall the place value of that column.

The $1$ is in the thousandths column.

Write the value of the digit.

The digit and the place value of the digit combine to give the value of the digit.

The value of the digit $1$ in the number $35.941$ is $1$ thousandths or $0.001$ or as a decimal fraction $\frac{1}{1000}.$

Example 6: thousandths

Write the value of $9$ in the number $835.219.$

Locate the digit within the number.

Recall the place value of that column.

The $9$ is in the thousandths place.

Write the value of the digit.

The digit and the place value of the digit combine to give the value of the digit.

The value of the digit $9$ in the number $835.219$ is $9$ thousandths or $0.009$ or as a decimal fraction $\frac{9}{1000}.$

Common misconceptions

Thousands or thousandths

Numbers to the right of the decimal point are parts of a whole and so they each end with ‘ths’. Numbers to the left of the decimal point do not end in ‘ths’ as they are whole numbers.

Practice decimal place value questions

0.01

one tenth

\frac{1}{100}

one

The digit $1$ is in the tenths column.

The value of the $1$ is $1$ tenth or $0.1$ or $\frac{1}{10}.$

$3$ hundreths

3

0.03

\frac{3}{10}

The digit $3$ is in the tenths column.

The value of the $3$ is $3$ tenths or $0.3$ or $\frac{3}{10}.$

0.004

0.4

\frac{4}{100}

$4$ tenths

The digit $4$ is in the hundredths column.

The value of the $4$ is $4$ hundredths or $0.04$ or $\frac{4}{100}.$

\frac{9}{1000}

$9$ thousandths

0.9

0.09

The digit $9$ is in the hundredths column.

The value of the $9$ is $9$ hundredths or $0.09$ or $\frac{9}{100}.$

\frac{2}{10000}

$2$ ten thousandths

0.02

$2$ thousandths

The digit $2$ is in the thousandths column.

The value of the $2$ is $2$ thousandths or $0.02$ or $\frac{2}{1000}.$

\frac{6}{1000}

$6$ hundreths

0.0006

\frac{6}{100}

The digit $6$ is in the thousandths column.

The value of the $6$ is $6$ thousandths or $0.06$ or $\frac{6}{1000}.$

Decimal place value GCSE questions

1. Use the number $56.973$ to answer the following questions.

(a) What is the digit in the tens place?

(b) Write down the value of the digit $7.$

(2 marks)

Show answer

(a) $5$

(1)

(b) $7$ hundredths or $0.07$ or $\frac{7}{100}$

(1)

2. (a) Write down the value of $3$ in the number $2.319.$

(b) Write down the value of $7$ in the number $58.107.$

(2 marks)

Show answer

(a) $3$ tenths or $0.3$ or $\frac{3}{10}$

(1)

(b) $7$ thousandths or $0.007$ or $\frac{7}{1000}$

(1)

3. (a) Calculate $0.328 \div 10.$

(b) Write down the value of $3$ in the answer to part (a).

(2 marks)

Show answer

(a) $0.0328$

(1)

(b) $3$ hundredths or $0.03$ or $\frac{3}{100}$

(1)

4. (a) Ben says,

“the value of the digit $9$ in $8.459$ is $9000”.$

Is Ben correct? Explain your answer.

(b) Callum says,

$“0.009$ is bigger than $0.08$ because $9$ is bigger than $8”.$

Is Callum correct? Explain your answer.

(4 marks)

Show answer

(a) No

(1)

Correct explanation involving thousandths

(1)

For example, Ben has said that the $9$ is in the thousands column when he meant to say the thousandths column or $0.009.$

(b) No

(1)

Correct explanation using the value of the digits $9$ and $8.$

(1)

For example, the $9$ in $0.009$ is worth $\frac{9}{1000}$ or $9$ thousandths.

The $8$ in $0.08$ is worth $\frac{8}{100}$ or $8$ hundreths.

So, $0.009$ is actually smaller in value than $0.08.$

5. In $2009$ the world record for the $100 \ m$ sprint was $9.69$ seconds.

Usain Bolt broke the world record for $100 \ m$ sprint.

Usain Bolt took $11$ hundreths of a second off the previous world record.

Work out the time Usain Bolt ran, setting the new world record for the $100 \ m$ sprint.

(2 marks)

Show answer

Subtracting $11$ hundredths from $9.69.$

(1)

$9.58$ seconds

(1)

Learning checklist

You have now learned how to:

Understand and use place value for decimals

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.