Summary Of ALL GCSE Maths Papers 2022: Question Analysis, Highlights & Next Steps

Originally published Wednesday 22nd June 2022

With the June 2022 series of GCSE maths exams now behind us, students will be winding down for the summer. However, at Third Space Learning, we’re continuing our series of posts analysing the GCSE maths papers in-depth and considering implications for preparing the next year’s cohort.

GCSE Maths 2024: Stay up to date

Join our email list to stay up to date with the latest news, revision lists and resources for GCSE maths 2024. We’ll be bringing in our expert contributors to analyse each paper and identify key topic areas to focus your revision.

GCSE 2024 dates
GCSE 2024 results (when published)
GCSE results 2023
Analysis of GCSE Maths Paper 1 (2023)
Analysis of GCSE Maths Paper 2 (2023)
Analysis of GCSE Maths Paper 3 (2023)
Summary of ALL GCSE Maths Papers (2023)

Highlights from the June 2022 maths papers

Short on time? Here’s what you need to know and share with your team!

• The Foundation series was generally well-received;
• Higher candidates found GCSE Maths Paper 1 very challenging, but GCSE Maths Paper 2 and GCSE Maths Paper 3 appeared more straightforward;
• The advance information married up almost seamlessly with the papers;
• There was no significant assessment of any topic not mentioned on the prerelease;
• The papers themselves ‘feel’ like a standard set of Edexcel papers;
• Exam adaptations narrowed the content but did not change the way it was assessed;
• There were some interesting topic crossovers, such as finding the volume of a cylinder from a 3D representation on Paper 1.

Exam adaptations were carried into November series

The exam adaptations made for the June 2022 series, namely the release of advance information and provision of a formula sheet, were continued for the November 2022 sitting. This ensured parity for students who re-sat in November, providing a similar set of circumstances to those they experienced in June 2022. Advance information for the November series was published on 27th June.

No adaptations in 2023 year: back to ‘business as usual’

The DfE stated on 10th May that exam adaptations would not apply for the 2022-23 academic year. There is no advance information to consider for the 2023 cohort of Year 11s – and we’re back to ‘business as usual’. However, it’s important to be mindful that the impact of the pandemic and lost learning time will have affected exam cohorts for several years to come.

---

This year’s papers didn’t depart from the norm

Exam adaptations aside, this year’s Edexcel papers haven’t felt particularly different. Patterns within papers, tiers and strands fit with previous years’ papers, and any percentage variations between topics are minor and within expectations.

I wrote two articles earlier in the year based on an analysis of the 2017-19 June and November series of papers and offered some teaching recommendations and exam preparation tips based on these. The June 2022 series does not change these recommendations significantly.

For example, within the Number strand at Foundation, we’ve seen further context-rich work on four operations and calculation skills, flexible application of proportional reasoning to a range of contexts, and procedural work on number properties such as factors and multiples, and topics such as standard form and error intervals.

Within the Shape strand at Higher, there is a continued emphasis on context-based problems within perimeter, area and volume, units and measurements, and Pythagoras and trigonometry – the latter was hit particularly hard in this series of papers.

• The GCSE Maths Topics Your Year 10 And Year 11 Should Revise For Their Foundation Exam
• Preparing For GCSE Higher Maths

Over the exam season, I blogged about each paper in some depth and considered how the advance information may appear on subsequent papers.

In this blog, I consider the exam series as a whole, taking a closer look in particular at which topics were assessed procedurally, and which included further complexity, such as solving problems in unfamiliar circumstances or real-life contexts.

Free GCSE maths revision resources for schools
As part of the Third Space Learning offer to schools, the personalised online GCSE maths tuition can be supplemented by hundreds of free GCSE maths revision resources from the secondary maths resources library including:
– GCSE maths past papers
– GCSE maths worksheets
– GCSE maths questions
– GCSE maths topic list

---

Keep the complexity measure in mind throughout

As usual, I’ve applied my complexity measure to the data.

• C1 – standard procedural problems, often worth one or two marks;
• C2 – problems asking candidates to explain their reasoning, interpret information from tables, diagrams or other contexts, or ‘show that’ type questions;
• C3 – non-standard multi-step problems, often requiring the application of skills from a variety of topics, worth three, four, or more marks.

As regular readers may already know, this isn’t a ‘difficulty’ measure. For example, simultaneous equations is one of the most difficult topics assessed on the Foundation tier, but the majority of problems are procedural, so would be categorised as C1.

What this measure does is help to direct focus for exam revision. We can see where it’s worth investing time in unfamiliar problems or contexts by targeting those topics most likely to assess in that way (e.g. proportional reasoning, shape, particularly perimeter, area and volume, context-based calculations, percentages and so on).

Read more:

• Question Level Analysis Of Edexcel Maths Past Papers (Foundation)
• Question Level Analysis Of Edexcel GCSE Maths Higher Past Papers

---

1. Foundation topic coverage similar to previous years overall

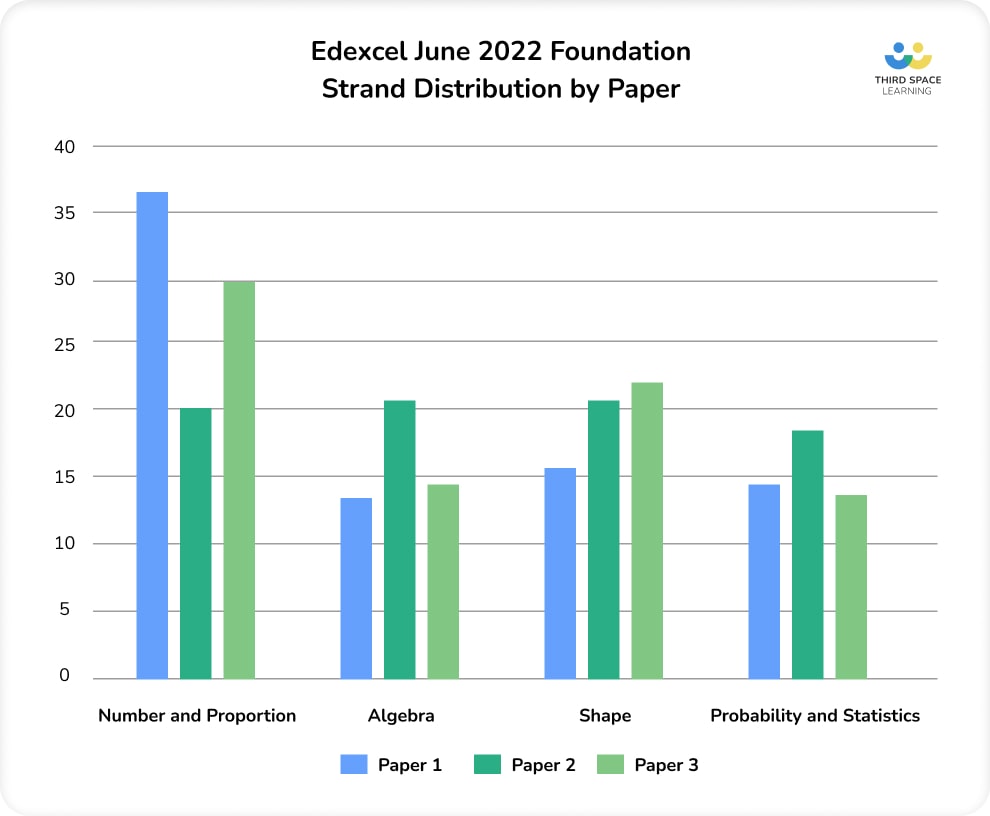
As is usual with Edexcel Foundation papers, the series had more marks available in Number and Proportion than in other strands; this was particularly true on the non-calculator Paper 1. While the advance information may have slightly narrowed content coverage, the balance across strands reflected patterns from earlier examination series.

Algebra and Shape proportions varied across the three papers, with the most Shape work on Paper 3. Typically, there is more Shape than Algebra work on Foundation, and this pattern has continued with this series of exams.

Number was the highest strand across the Foundation papers

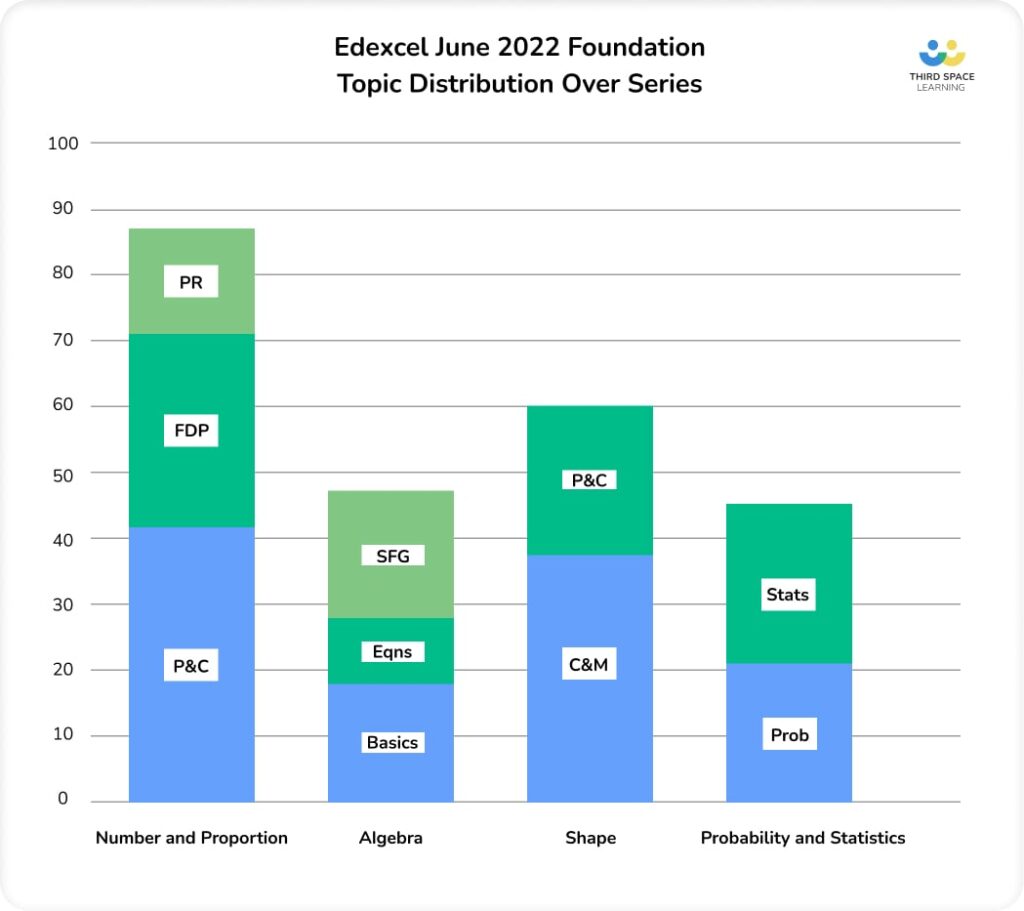
Topic strands: Number and Proportion

Examining each strand further, we see approximately half (48%) of the marks within Number and Proportion for properties and calculations – including integer calculations, rounding, place value and so on. There was very limited assessment of powers and roots.

Topic strands: Algebra

44% of the marks within Algebra were in sequences, functions and graphs, a slightly higher proportion than on some previous series, but within usual percentage variations. In particular, there was a lot of work on coordinates and sequences.

Topic strands: Shape

Calculations and measures, and properties and constructions, were more fairly balanced than in some previous series, such as in June 2019 when almost three-quarters of the marks were for calculations and measures. This is mostly due to comparatively heavy assessment of 2D shape and angle properties, with problem-solving questions on angles in parallel lines, within polygons, and other angle facts.

Topic strands: Probability and Statistics

Probability and Statistics were quite evenly balanced when considering the series as a whole, although Paper 2 had quite a bit more Statistics than Probability.

Foundation June series continued more balanced topic distribution

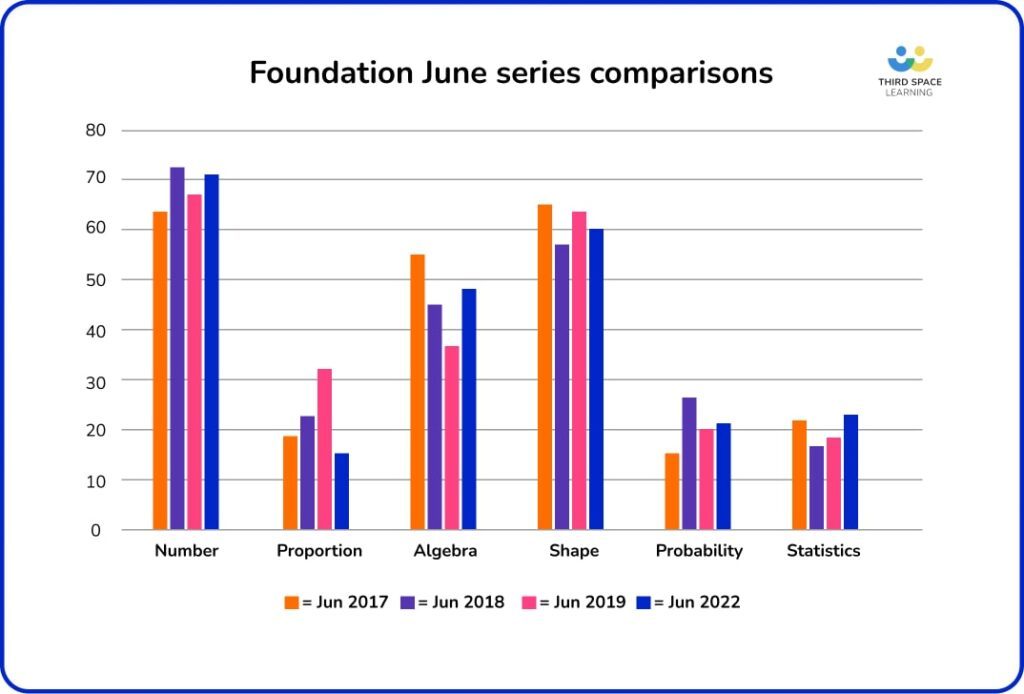
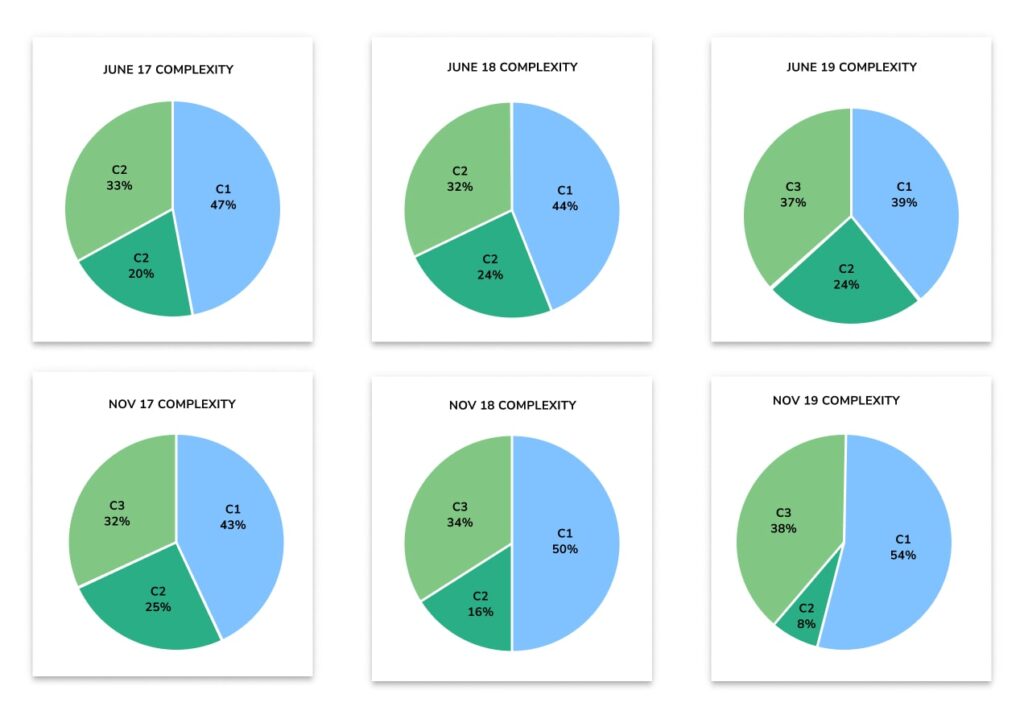
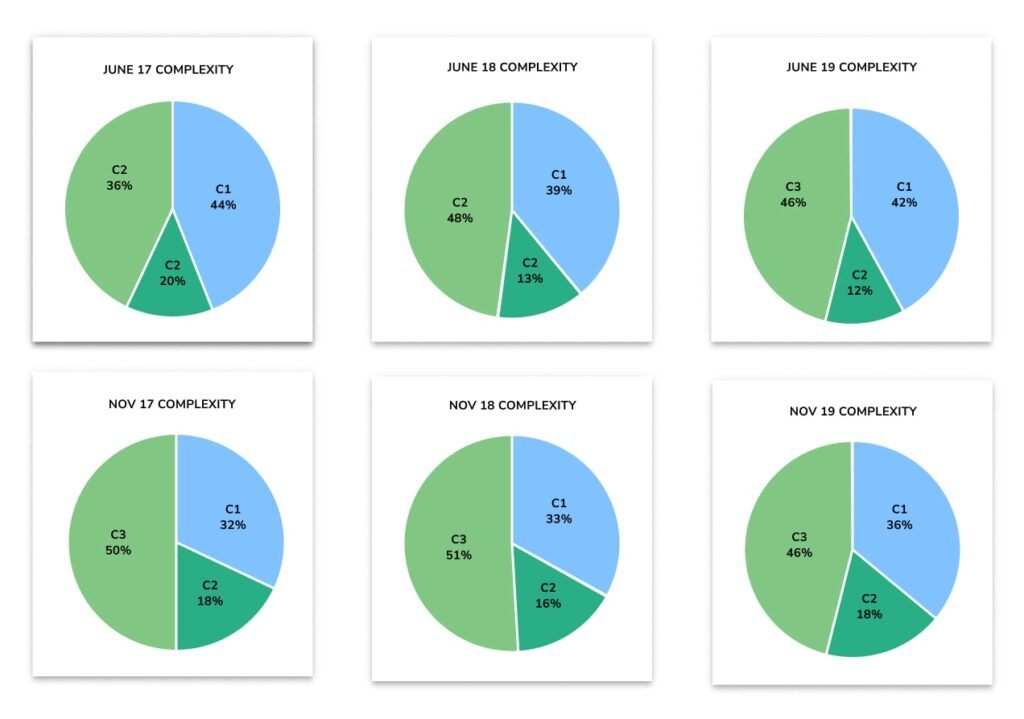
I noted in my 2017-19 Foundation analysis that the November paper series (particularly Nov-18/19) favoured a higher ratio of C1 to C2 questions, with the June series being slightly more balanced. The June 2022 series continues this pattern at Foundation, so it will be interesting to see what happens with this year’s November series.

Foundation series complexity doesn’t equal difficulty

The complexity measure graph is closest to the June 2017 series, indicating that this isn’t necessarily a measure of the perceived difficulty of the exam. Students found the June 2017 series very difficult, but the reception for June 2022 was generally positive. 

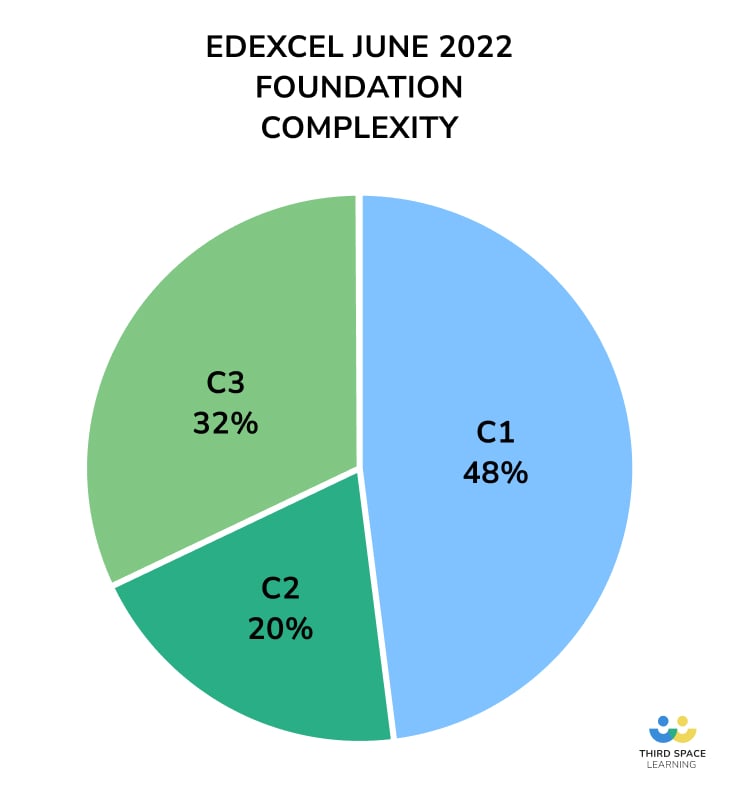
What was missing from the 2022 Foundation papers?

This is not an exhaustive list, but some of the things that weren’t examined in any of the three Foundation papers include:

• Significant explicit work on order of operations
• Systematic listing strategies
• Representing inequalities on a number line
• Expanding and factorising standard quadratic expressions (binomial brackets)
• Solving standard quadratic equations by factorising
• Cubic and reciprocal functions and their graphs
• Finding missing sides/angles using right-angled trigonometry 
• Standard compass and ruler constructions 
• Congruent triangle criteria
• Arc lengths and areas of sectors
• Scatter graphs

Many of these topics are underlined content on the GCSE specification, meaning that they are topics directed at the top end of the Foundation paper (and often appear in crossover content). As such, there is not enough room for assessment of each of these on every exam. However, the fact that they haven’t appeared in this series increases the chance of them appearing next time. However, this is not a guarantee, and we should be wary of over-interpretation!

Foundation paper complexity continued to reflect previous years

Generally, the complexity measure graphs for Foundation continue to reflect patterns from previous series: a heavy weighting towards Number and Proportion content, with lots of problem-solving in the latter, a slightly higher proportion of Shape work when compared to Algebra, and most of the Algebra, Statistics and Probability content assessed procedurally.

Complexity: Number and Proportion

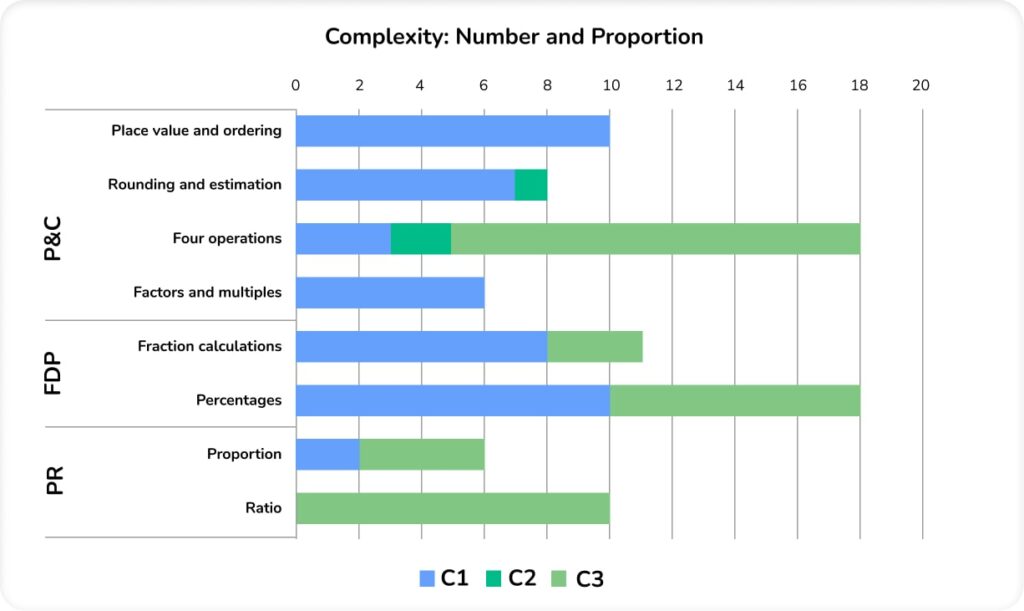
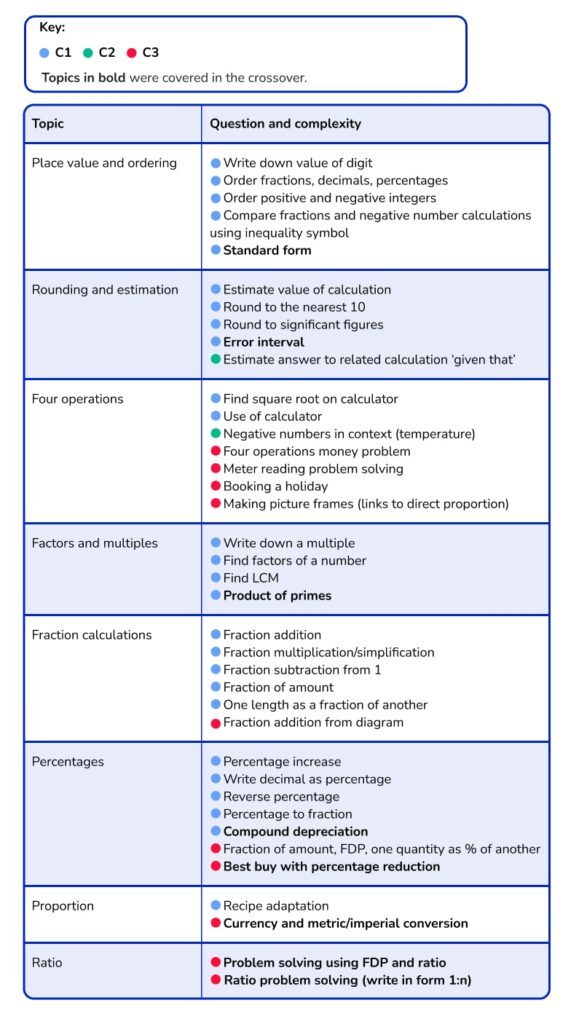
Continuing the pattern from previous series, some topics within the ‘Number and Proportion’ strand attracted a significant number of C3 marks. The majority of four operations work asked candidates to solve multi-step problems featuring real-life contexts, and most of the work on proportion (and all of the work on ratio) was C3.

In contrast, there were plenty of C1 marks available in the following topics: place value and ordering, rounding and estimation, factors and multiples, and fraction calculations.

Complexity: Algebra

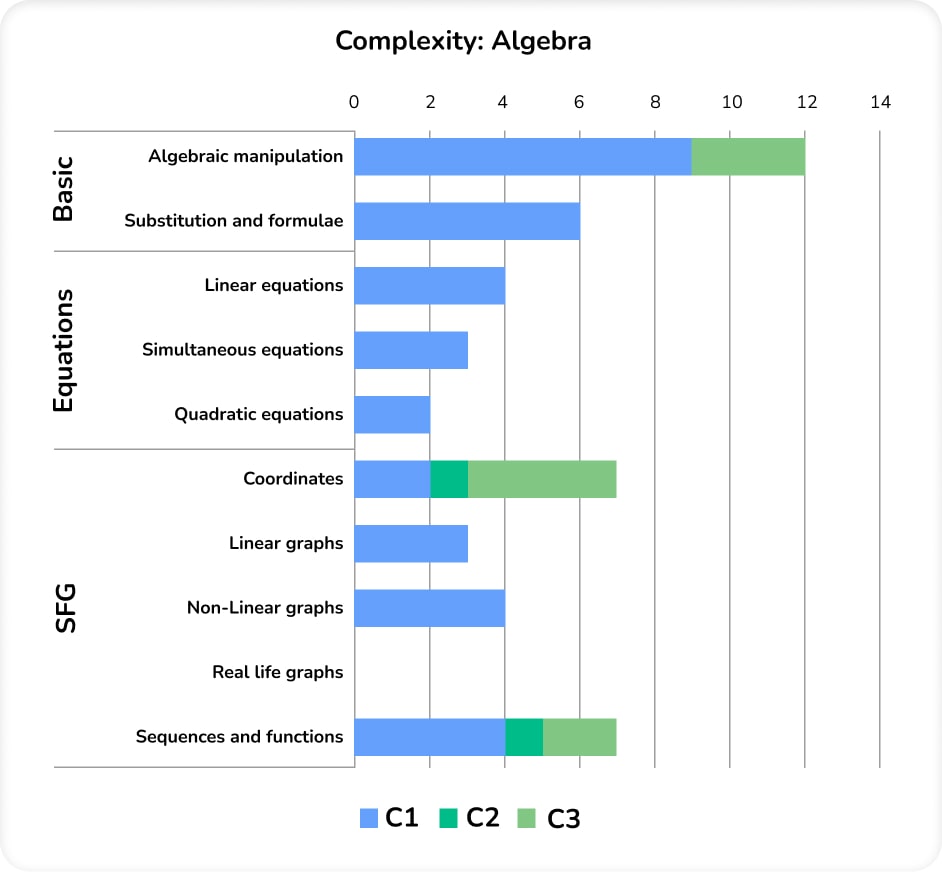
Algebra was generally assessed in a procedural manner, as is typical for the Foundation series. Most of the C3 content appeared in the crossover questions; these were the area of trapezium/algebraic expressions question on Paper 3, and the coordinates question on Paper 1.

Standard quadratic expressions (i.e. expanding or factorising double brackets) didn’t appear on any of the three papers. The quadratic equation on Paper 1 was a root estimation from a quadratic graph.

Complexity: Shape

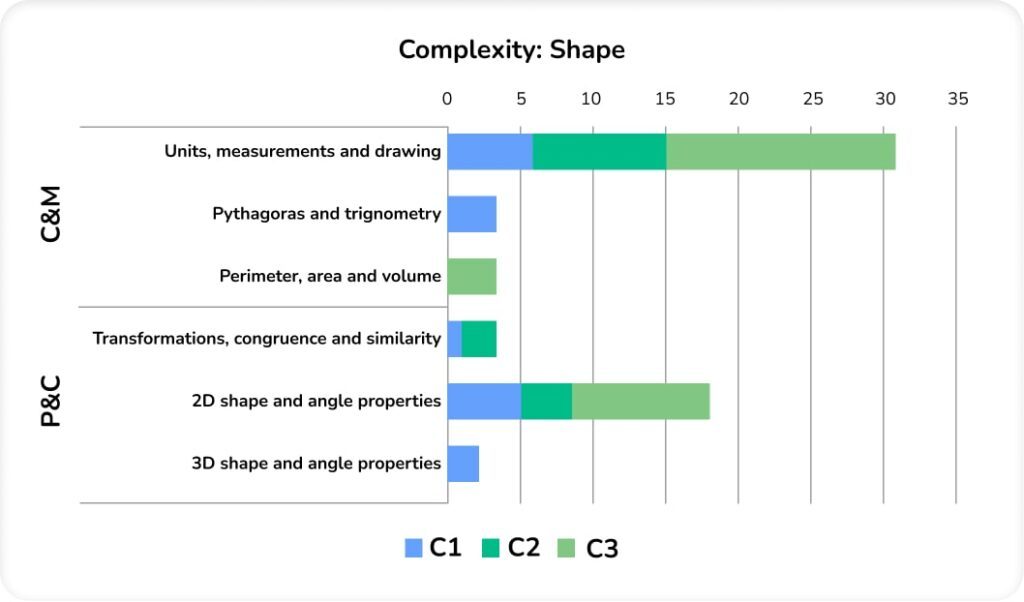
There was comparatively little perimeter, area and volume in this series. Some were assessed in context (such as the area of trapezium/algebraic expressions question) and are accounted for elsewhere, but even taking this into account, the proportion is low.

Pythagoras and trigonometry are also low, but this is probably to be expected, given its position as one of the most challenging topics on the Foundation syllabus.

There was very limited work on vectors, except potentially in the question asking students to describe a translation. Again, perhaps a conscious decision by the exam boards given the level of challenge and lost learning time due to the pandemic.

Complexity: Probability and Statistics

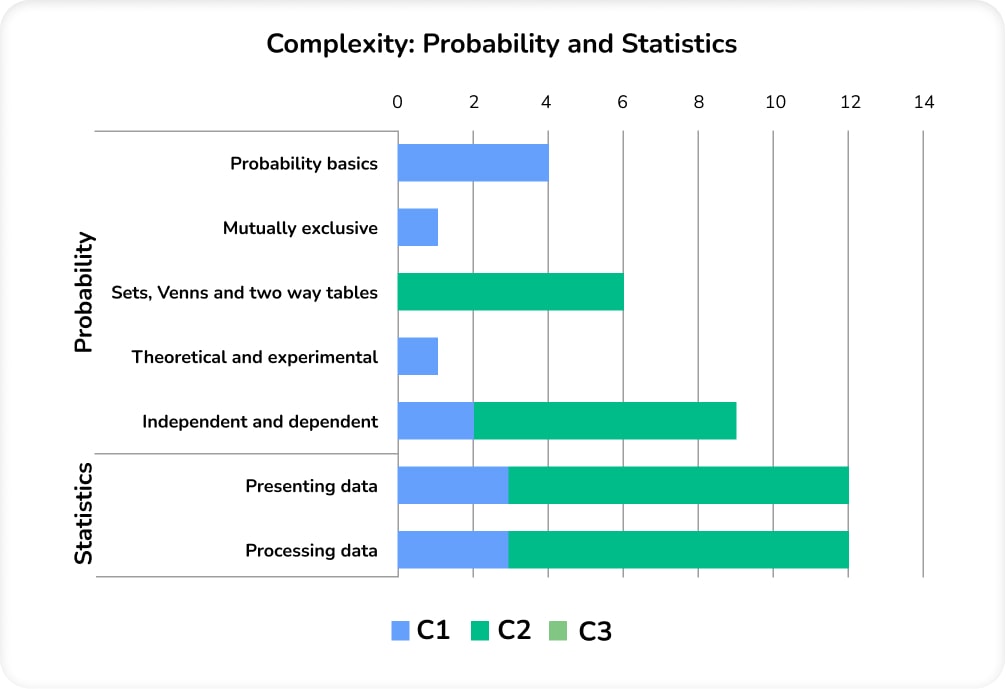
Lots of the Foundation Statistics content was C2. This is not a particularly significant observation, and is more a function of my complexity classification, as Statistics involves lots of interpreting or reading from charts and tables. The majority of the Probability and Statistics work was accessible and procedural, leading students well through the problems.

I commented on my 2017-19 analysis that frequency trees appeared popular on Foundation. This trend has continued with another frequency tree (and a standard tree diagram!) in this series.

It’s also worth noting that only one question was included in the crossover content; there is limited overlap between Foundation and Higher on these strands.

---

2. Higher topic coverage was fairly distributed overall

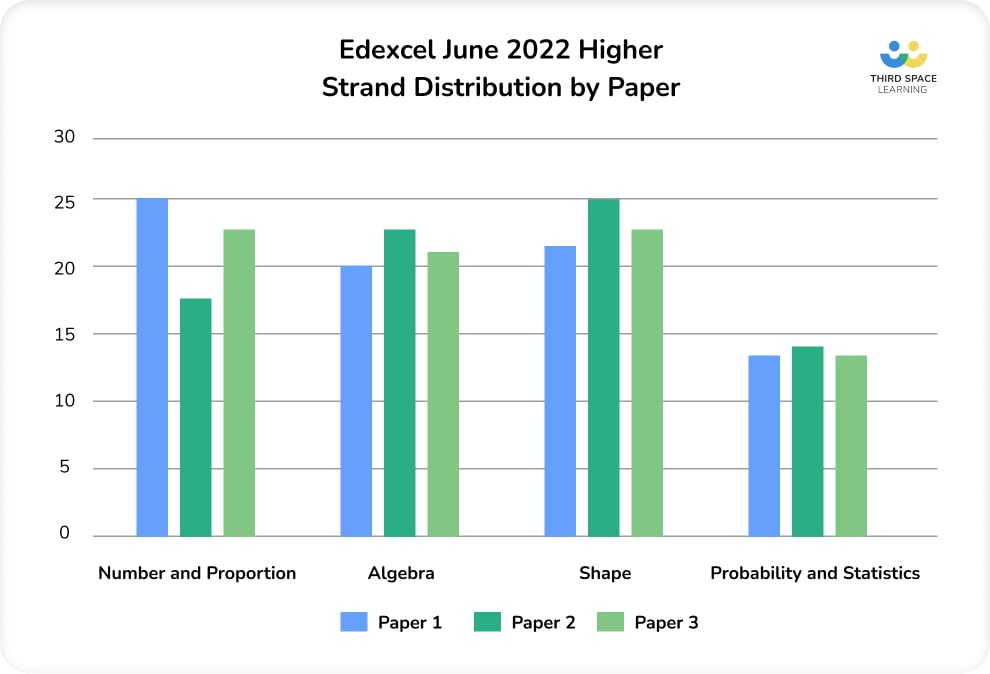
Despite the advance information narrowing some of the content coverage, there was still a fair distribution of topics across the three papers.

As usual, there was more Number and Proportion on Paper 1, with more Algebra and Shape on Papers 2 and 3, as is to be expected for the assessment of non-calculator numerical work on the first paper.

Algebra and Shape were assessed in roughly similar proportions across the three papers, but with slightly more Shape than Algebra content overall.

Topic strands more evenly distributed across Higher papers

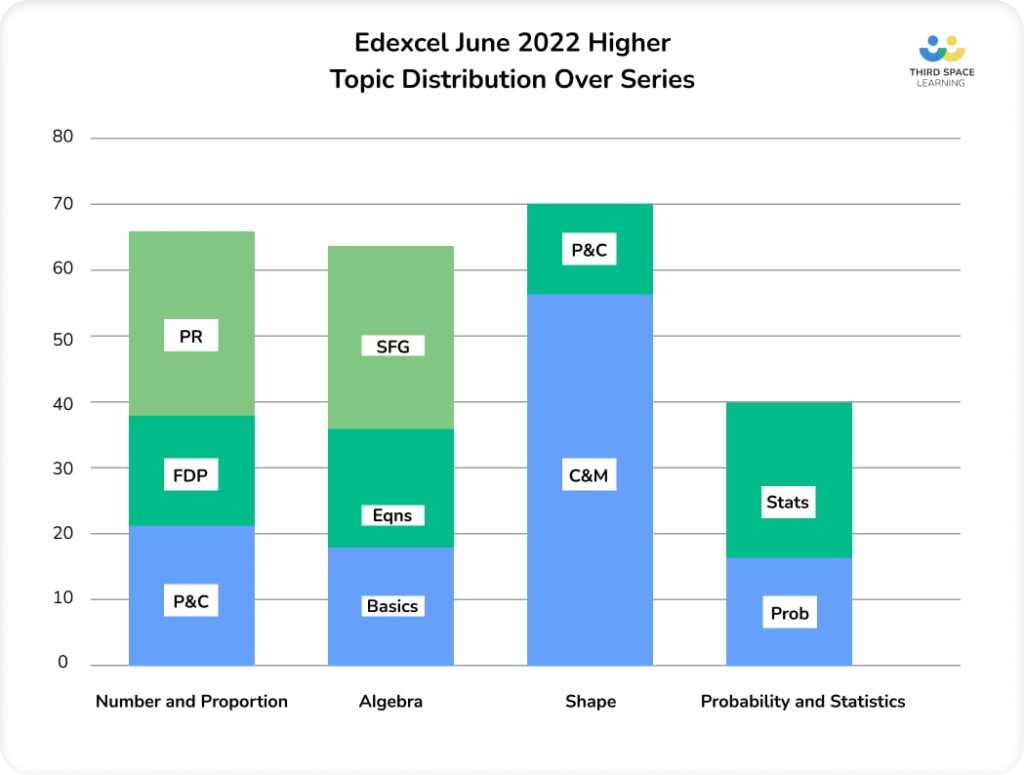
Topic strands: Number and Proportion

Number and Proportion were similarly well-balanced, with a fairly even split between properties and calculations, fractions, decimals and percentages, and proportional reasoning.

Topic strands: Algebra

Algebra appeared in similar proportions to previous series, with over 40% of the Algebra marks on sequences, functions and graphs, the latter of the three being particularly hard-hit.

Topic strands: Shape

The majority of Shape marks were for calculations and measures. This is perhaps unsurprising with 17/240 (7%) of the overall marks for Pythagoras and trigonometry and 16/240 (~7%) for perimeter, area and volume.

Topic strands: Probability and Statistics

There was more Statistics than Probability, with the majority of the Statistics marks (16/240, ~7%) for presenting data, so drawing and interpreting charts and graphs. Within Probability, the majority of the marks were from questions on Venn diagrams and independent/dependent events problems.

Higher topic distribution followed similar patterns to June 2019

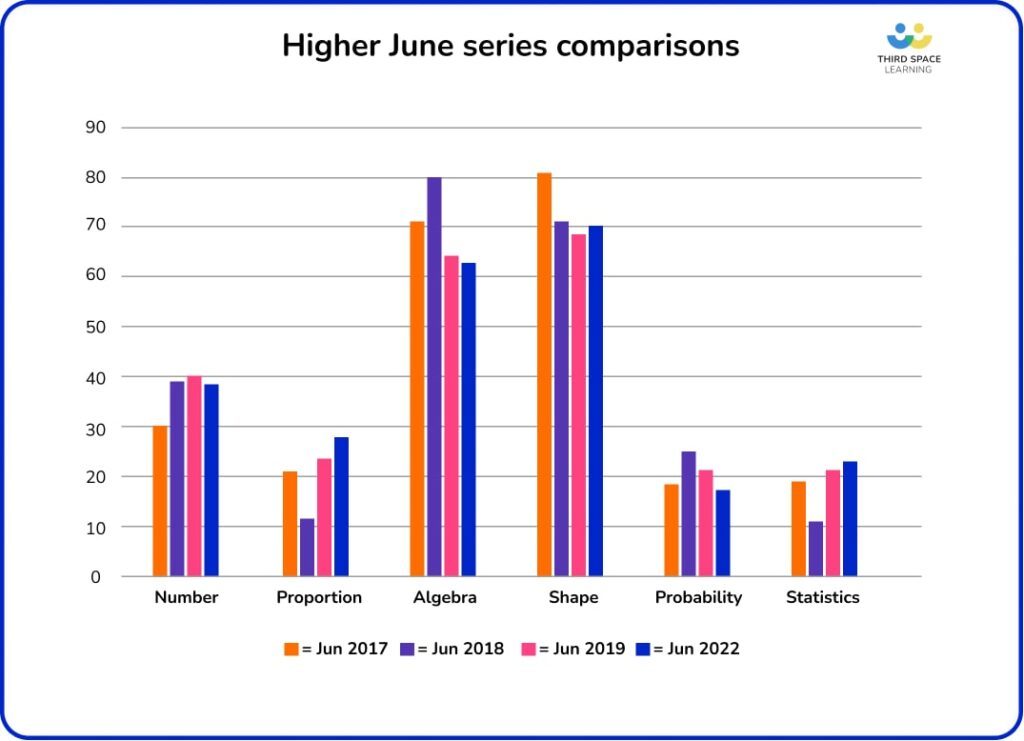
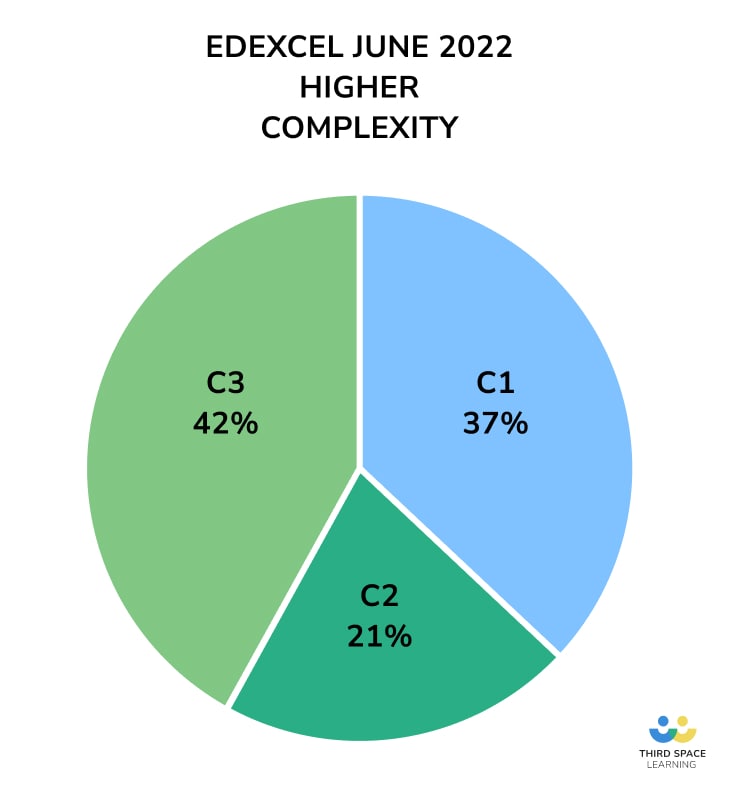
Higher complexity also similar to previous June series

The complexity measure shows a similar pattern to previous June series, although there is a slightly larger proportion of C2 questions (and consequently a smaller proportion of C1 and C3 questions) than we’ve seen before. 

What was missing from the 2022 Higher papers?

Again, this is not an exhaustive list, but the things that jumped out at me were:

• Surd laws and rationalising the denominator
• Highest common factor/lowest common multiple
• More standard linear equations/inequalities (nearly all assessed in context)
• Explicit assessment of completing the square, use of CTS to find turning points
• Solving a system of two linear simultaneous equations
• Cubic and reciprocal graphs
• Sequences – linear, quadratic and other types
• Algebraic proof
• Standard compass and ruler constructions
• Scatter graphs

While this does not guarantee the inclusion of these topics in the next series of papers, we should be aware when preparing students that these may now be more likely to be assessed.

A running theme: Higher paper complexity followed previous patterns

Generally, the complexity measure graphs for Higher continue to reflect patterns from previous series: procedural Number, more problem-solving in Proportion and Shape, and a mix of the two in Algebra, Statistics and Probability.

Complexity: Number and Proportion

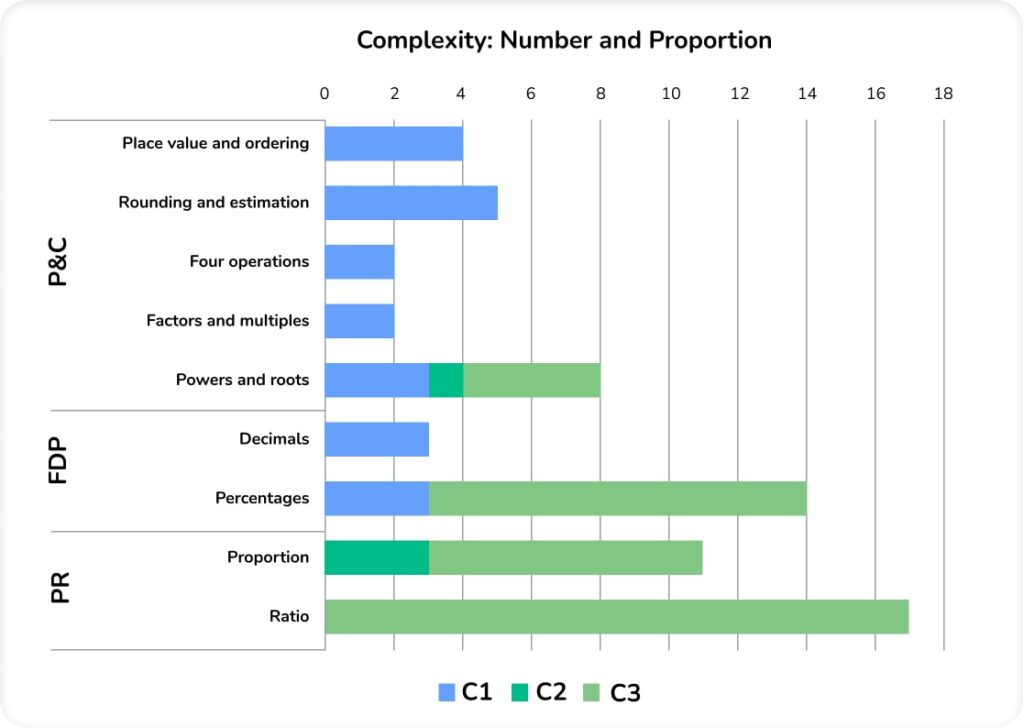
In Number and Proportion, there’s a dramatic split between procedural C1 Number problems, particularly within properties and calculations, and more in-depth C3 problems to solve within percentages, ratio and proportion.

With 17 marks (7% of the overall exam), ratio problem solving is definitely one to hit with Higher candidates in the future. With the exception of one 2-mark question, linear equations and inequalities weren’t assessed on this series of Higher papers as a standalone topic, but many of the ratio problems led students towards forming equations to solve.

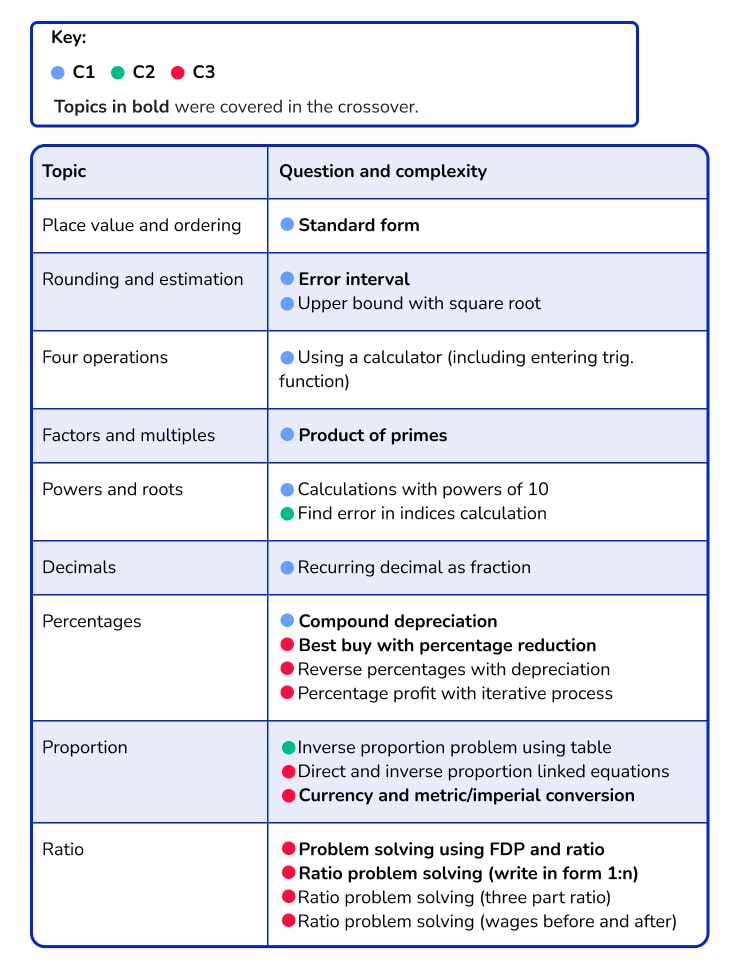
Complexity: Algebra

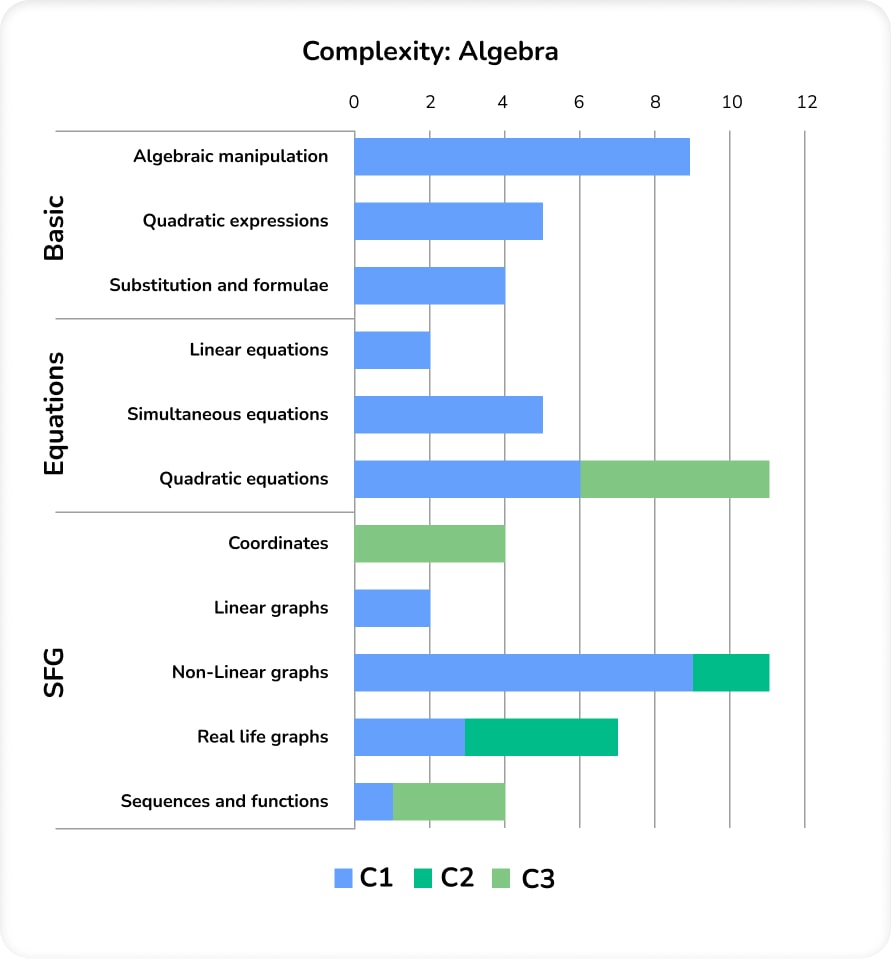
In comparison with previous series, the Algebra content on June 2022 Higher was assessed in a more procedural manner. The Algebra content on the second and third papers, in particular, didn’t include a lot of ‘tricks’ or sneaky bits and felt quite fair to candidates.

It is unclear whether this is a conscious decision on the part of the exam board to reflect the disturbances to candidates’ education over the past two years as a result of the pandemic or just a curiosity of this set of papers.

Coordinates appeared as problem-solving on Paper 1, as is typical for Higher level. The balance between C1 and C3 on quadratic equations also reflects previous series. Non-linear graphs are featured very highly in this set of papers.

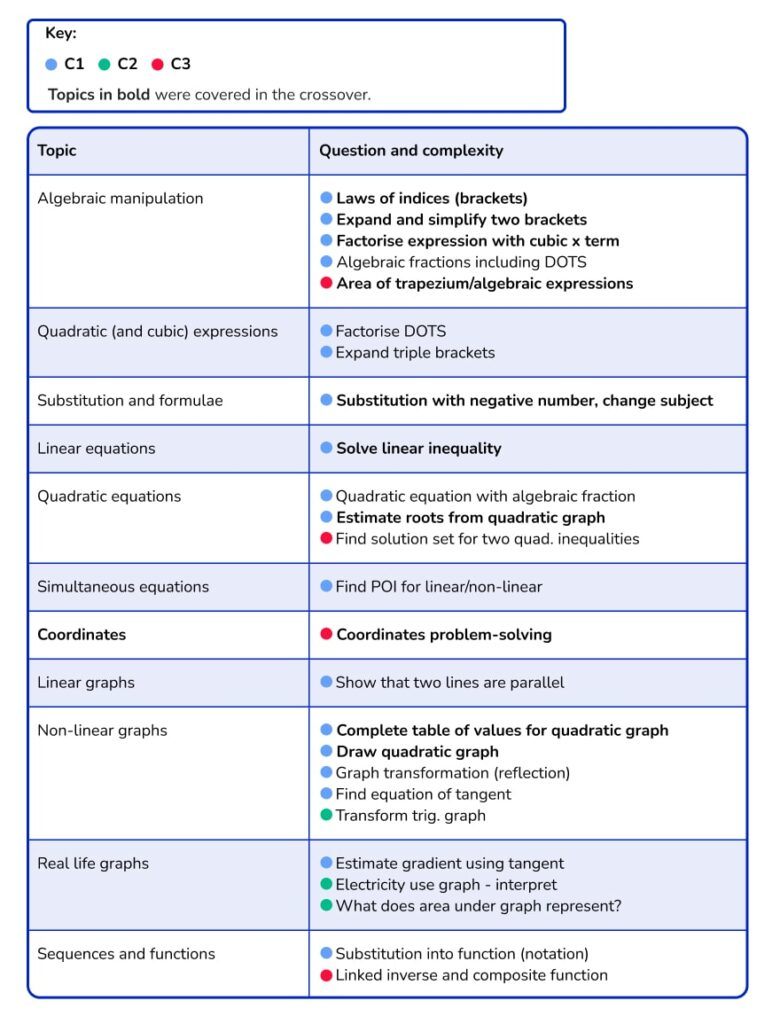
Complexity: Shape

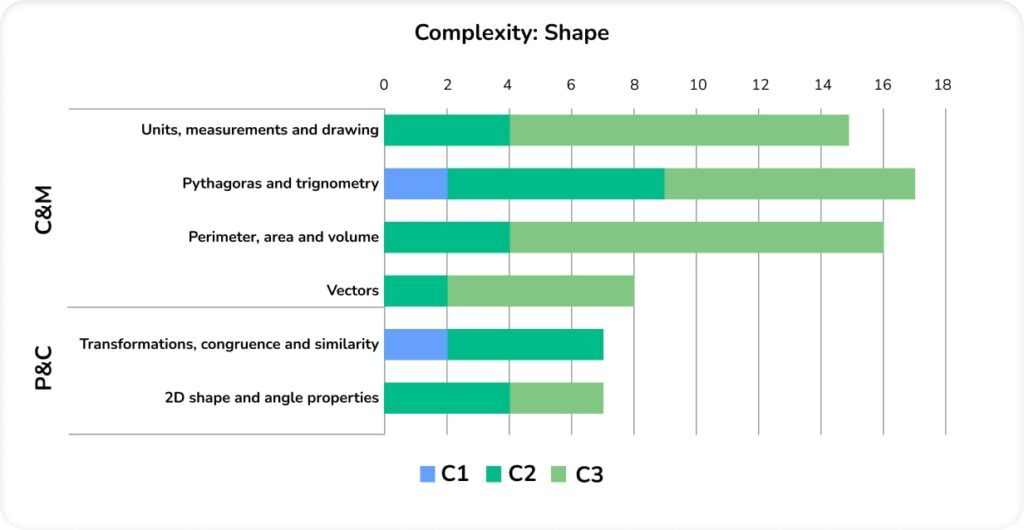
The overwhelming majority of Shape work on Higher was C2 or C3 questions; multi-step unfamiliar problems, proofs and reasoning (a pattern that is common in Higher exam series).

Within properties and constructions, we were missing any significant assessment of 3D shape properties or constructions. The former is not unusual for Higher as this topic includes plans, elevations and standard naming/labelling conventions, traditionally considered ‘lower-grade’ topics.

The omission of constructions may have been a pandemic-based adaptation to avoid disadvantaging students who may not have had access to the correct equipment during home learning. But, then again, constructions don’t necessarily appear on every Higher series anyway.

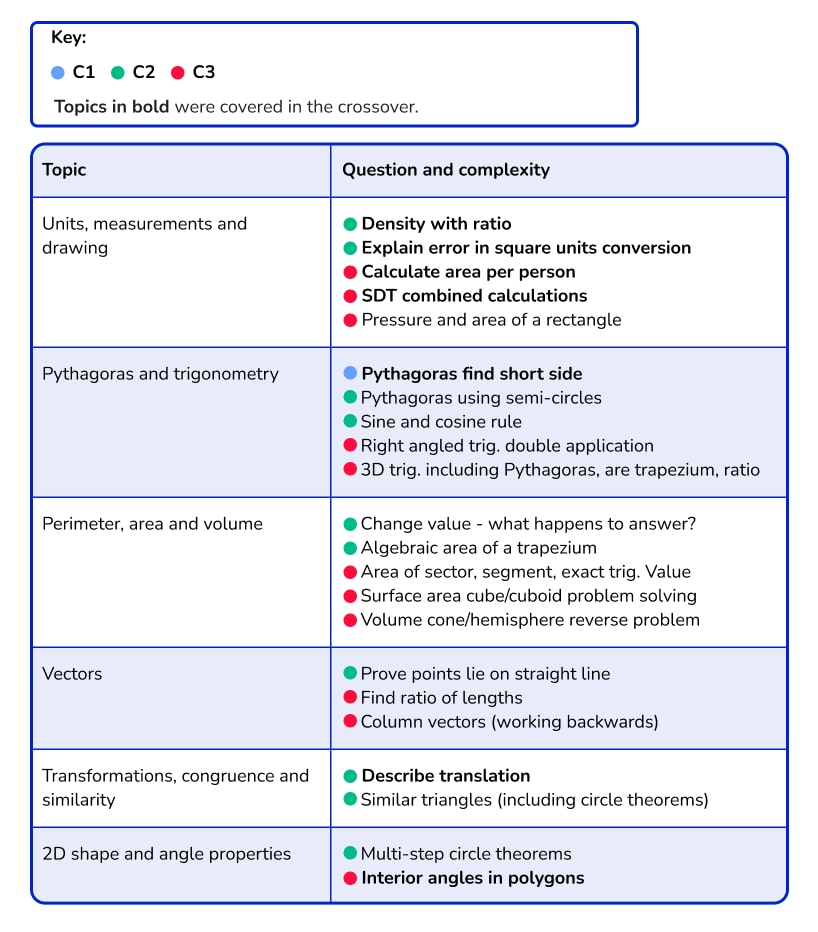
Complexity: Probability and Statistics

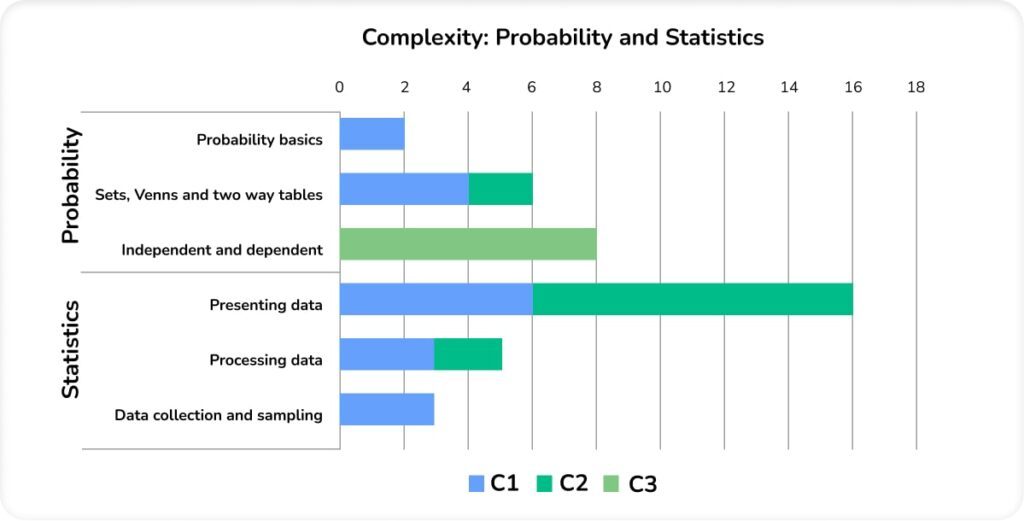
Marks in the Probability strand at Higher level mostly came from Venn diagrams and independent and dependent events. One surprising thing about this series was that both questions on independent and dependent events were less structured, unfamiliar problems.

The majority of content in Statistics was in presenting data, and more in favour of interpreting or criticising graphs than drawing them, although students were asked to draw both a histogram and a cumulative frequency graph. This series also saw the first assessment of capture-recapture, a new topic to Edexcel GCSE for 2015.

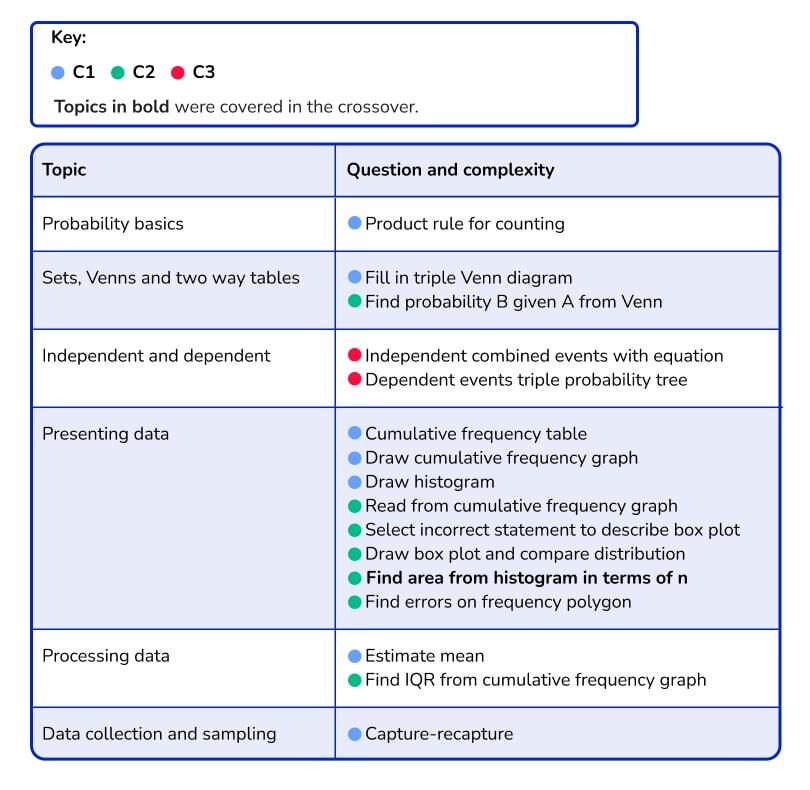
3. Implications and recommendations for teaching next year

To summarise, the June 2022 series looks much like any other set of Edexcel exam papers. On Higher, students found the first paper relatively difficult, but the next two were more accessible. Foundation seemed generally well-received.

As a teacher, how should you act on the preceding information? Let’s look at a few key recommendations that might influence your teaching next year!

Pandemic affected the next cohort, though they won’t have adaptations

As we return to ‘exams-as-usual’, my key takeaway from this is to continue to be mindful of pandemic disruptions in the next few cohorts of students.

Next year’s cohort of Year 11s will sit papers across the complete spectrum of content with no advance information. Therefore, it is crucial to continue plugging gaps via low-stakes assessment and adaptations of schemes of learning.

Third Space Learning’s online, one-to-one GCSE revision tuition can help identify gaps in learning and help students to prepare for the exams. Third Space Learning also offers a wide range of resources to support students in their studies, take a look at our popular Fluent in Five pack!

Preparing next year’s GCSE maths students

Foundation students

For Foundation students, include lots of context-based problems on:

• Four operations
• Fractions
• Percentages
• Proportional reasoning

Continue to work on procedural algebra, but be aware that we’ve seen more applications on this series of papers, such as the trapezium/algebraic expressions question on Paper 3; give students an opportunity to tackle problems like this in the classroom.

Higher students

For Higher students, ensure that algebra skills are automatic. They need to be able to problem-solve using their algebra toolkit without expending too much mental energy on how the mechanics of the procedures work.

I’d take a look at some of the problems on Paper 1 that caused upset; the overlapping circles and the Pythagoras’ theorem with semicircles would be a good place to start.

Resilience with Higher students is incredibly important. With the back half of the paper directed at grade 7+, they need to expect questions they won’t be able to answer fully and need practice at ‘working like detectives’ to find something they can attempt.

---

4. Next steps for GCSE maths teaching

So, how can you make good use of this information over the last few weeks of term?

• Incorporate some of the more challenging problems from this series of exams into teaching materials for the next cohort of Year 11s. It can often be helpful to look at repeated variations of these problems (i.e. change the numbers);
• Look for ways to include less-standard topic crossovers more frequently in teaching content. The site Interwoven Maths is a fantastic resource for these types of questions;
• Act on student feedback. Which questions did your 2022 year 11s find difficult on the exams and how could current learning materials be adapted to plug these gaps?
• In preparation for results, think about how you will use question-level analysis for your cohort. There may be specific gaps in teaching within your department that are not reflected nationwide, which may represent a need for departmental CPD or sharing of good practice on key topics.

Free GCSE maths revision resources for schools
As part of the Third Space Learning offer to schools, the personalised online GCSE maths tuition can be supplemented by hundreds of free GCSE maths revision resources from the secondary maths resources library including:
– GCSE maths past papers
– GCSE maths worksheets
– GCSE maths questions
– GCSE maths topic list