Mean in Math - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Addition and subtraction Multiplication and division Decimals Rounding numbers

Math resources Statistics and probability Average in math

Mean in math

Here you will learn about the mean, including what the mean is and how to find the mean.

Students will first learn about the mean in math as part of statistics and probability in $6$ th grade.

What is the mean in math?

The mean in math, specifically the arithmetic mean, is a type of average calculated by finding the total of the values and dividing the total by the number of values.

$\text{Mean}=\cfrac{\text{total}}{\text{number of values}}$

For example,

Calculate the mean of $3, \, 8, \, 10, \, 11$ and $13.$

$\text {Mean }=\cfrac{\text { total }}{\text { number of values }}=\cfrac{3+8+10+11+13}{5}=\cfrac{45}{5}=9$

$9$ is the mean of the data set.

This value, also known as the population mean, is a measure of central tendency. It summarizes a data set (population) with a single point. Median and mode are also measures of central tendency.

[FREE] Averages and Range Worksheet (Grade 6)

Use this quiz to check your 6th grade students’ understanding of averages and range. 10+ questions with answers covering a range of 6th grade averages and range topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Averages and Range Worksheet (Grade 6)

DOWNLOAD FREE

While all three measure center in some way, they are not the same. Mean can be thought of as sharing equally between all data points.

For example,

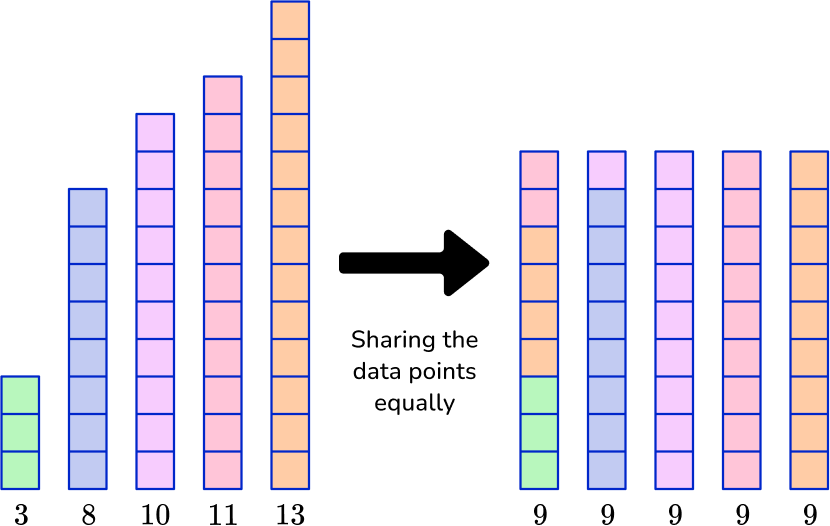
It is also important to consider that the number of observations (number of data points) changes how much each data point affects the mean.

For example,


Data set $A\text{: } 2, 3, 10$	Data set $B\text{: } 2, 2, 3, 3, 10, 10$
Mean: $15 \div 3 = 5$	Mean: $30 \div 6 = 5$

Now add the data point $10$ to each data set and recalculate the mean.


Data set $A\text{: } 2, 3, 10, 10$	Data set $B\text{: } 2, 2, 3, 3, 10, 10, 10$
Mean: $25 \div 4 = 6.25$	Mean: $40 \div 7 = 5.7$

Notice that the mean in data set $A$ grew by $1.25,$ while the mean of data set $B$ grew by $0.7.$

Since there are less data points in $A$ , adding (or taking away) a data point impacts the mean more than in a data set with more points, like data set $B.$

What is the mean in math?

$What is the mean in math?$

Common Core State Standards

How does this relate to $6$ th grade math?

Grade 6 – Statistics and Probability (6.SP.A.3)
Recognize that a measure of center for a numerical data set summarizes all of its values with a single number, while a measure of variation describes how its values vary with a single number.

How to calculate the mean in math

In order to calculate the mean in math:

Find the sum of the data points.
Divide the sum by the number of data points.
Write down the answer.

Mean in math examples

Example 1: finding the mean

Calculate the mean value of this list of numbers:

$2 \quad 7 \quad 9 \quad 10 \quad 12$

Find the sum of the data points.

$2+7+9+10+12=40$

2Divide the sum by the number of data points.

There are $5$ values in the data set. Divide the total by $5.$

$\text{Mean}=\cfrac{\text{total}}{\text{number of values}}=\cfrac{40}{5}=8$

3Write down the answer.

The mean is $8.$

Example 2: finding the mean

Calculate the mean value of this set of numbers to the nearest tenth.

$13 \quad 16 \quad 17 \quad 17 \quad 18 \quad 20$

Find the sum of the data points.

$13+16+17+17+18+20=101$

Divide the sum by the number of data points.

There are $6$ values in the data set. Divide the total by $6.$

$\text{Mean}=\cfrac{\text{total}}{\text{number of values}}=\cfrac{101}{6}=16.8333…$

Write down the answer.

$16.8333\dots$ to the nearest tenth is $16.8.$

$16.8$ is the mean.

Example 3: finding the mean

Calculate the mean value of this set of data to the nearest hundredth.

$11 \quad 13 \quad 14 \quad 15 \quad 19 \quad 20 \quad 22$

Find the sum of the data points.

$11+13+14+15+19+20+22=114$

Divide the sum by the number of data points.

There are $7$ values in the data set. Divide the total by $7.$

$\text{Mean}=\cfrac{\text{total}}{\text{number of values}}=\cfrac{114}{7}=16.2857…$

Write down the answer.

$16.2857\dots$ rounded to the nearest hundredth is $16.29.$

$16.29$ is the mean.

Example 4: finding the mean

Calculate the mean value of this list of numbers.

$101 \quad 102 \quad 105 \quad 106 \quad 108$

Find the sum of the data points.

$101+102+105+106+108=522$

Divide the sum by the number of data points.

There are $5$ values in the data set. Divide the total by $5.$

$\text{Mean}=\cfrac{\text{total}}{\text{number of values}}=\cfrac{522}{5}=104.4$

Write down the answer.

$104.4$ is the mean.

How to solve a problem involving the mean in math

In order to solve a problem involving the mean in math:

Use the mean and number of values to find the total.
Find the sum of the known data points.
Subtract the sum of the known data points from the first total to find the missing data point.

Problem solving involving mean examples

Example 5: problem solving

The mean of $4$ values is $10.$

Here are $3$ of the values:

$6 \quad 9 \quad 12$

Find the $4^{th}$ value.

Use the mean and number of values to find the total.

The mean of $4$ values is $10.$ Multiply these together to find the total of the $4$ numbers.

$\text{Total of 4 values}=\text{mean} \times \text{number of values}=10\times 4=40$

Find the sum of the known data points.

$\text{Total of 3 values}=6+9+12=27$

Subtract the sum of the known data points from the first total to find the missing data point.

$40-27=13$

The $4^{th}$ value is $13.$

Alternatively, you could use the equation for finding the mean. You could use $x$ as the missing value.

Then rearrange and solve.

$\begin{aligned} \text{Mean} &= \cfrac{\text{total}}{\text{number of values}}\\\\ 10&=\cfrac{6+9+12+x}{4}\\\\ 10 &= \cfrac{27+x}{4}\\\\ 40&=27+x\\\\ 13&=x \end{aligned}$

Example 6: problem solving

The mean of $5$ values is $14.$

Here are $4$ of the values:

$5 \quad 11 \quad 13 \quad 19$

Find the $5^{th}$ value:

Use the mean and number of values to find the total.

The mean of $5$ values is $14.$ Multiply these together to find the total of the $5$ numbers.

$\text{Total of 5 values}=\text{mean} \times \text{number of values}=14\times 5=70$

Find the sum of the known data points.

$\text{Total of 4 values}=5+11+13+19=48$

Subtract the sum of the known data points from the first total to find the missing data point.

$70-48=22$

The $5^{th}$ value is $22.$

Alternatively, you could use the equation for finding the mean. You could use $x$ as the missing value. Then rearrange and solve.

$\begin{aligned} \text{Mean} &= \cfrac{\text{total}}{\text{number of values}}\\\\ 14&=\cfrac{5+11+13+19+x}{5}\\\\ 14 &= \cfrac{48+x}{5}\\\\ 70&=48+x\\\\ 22&=x\\\\ \end{aligned}$

Teaching tips for mean in math

Introduce mean with countable objects (like counters or connecting cubes). This will allow students to physically add all the data points together and then share them equally – matching the procedure for the mean. Doing a hands-on activity like this helps students make sense of what the mean represents and understand why the procedure to find mean works.

Worksheets can be useful for teaching mean, but be sure to include a variety of question types – ones with mean missing, ones with a data point missing and a mixture of number types, such as fractions, decimals and integers.

Easy mistakes to make

Confusing the mean and the median
They are both average values, but do not represent the same average and are found in different ways. The median is the middle number (middle value) when the data set is arranged in ascending (or descending) order. The mean is a number that represents the data points equally shared and is found by adding all the values and then dividing by the number of data points.

Forgetting the mean can be a decimal
The mean does not have to be a whole number. It can be a decimal or a fraction. It may be a decimal which needs rounding.

Thinking the mean has to be a number in the data set
While the mean can be a number in the data set, often it is not. Adding the data points together and then dividing them by the number of data points allows for the mean to be a number outside of what is in the data set.

Practice mean in math questions

7

7.4

7.5

8

First calculate the sum of the numbers in the given set.

$5+7+8+8+9=37$

Then divide the sum by the number of data points.

$\begin{aligned} \text{Mean}&= \cfrac{\text{total}}{\text{number of values}}\\\\ \text{Mean}&=\cfrac{5+7+8+8+9}{5}\\\\ \text{Mean}&= \cfrac{37}{5}\\\\ \text{Mean}&=7.4\\\\ \end{aligned}$

5.9

5.8

5.75

5.7

First calculate the sum of the values.

$3+5+6+9=23$

Then divide the sum by the number of data points.

$\begin{aligned} \text{Mean}&= \cfrac{\text{total}}{\text{number of values}}\\\\ \text{Mean}&=\cfrac{3+5+6+9}{4}\\\\ \text{Mean}&= \cfrac{23}{4}\\\\ \text{Mean}&=5.75\\\\ \end{aligned}$

9.16

9.5

10

9.17

$\begin{aligned} \text{Mean}&= \cfrac{\text{total}}{\text{number of values}}\\\\ \text{Mean}&=\cfrac{7+8+9+10+10+11}{6}\\\\ \text{Mean}&= \cfrac{55}{6}\\\\ \text{Mean}&=9.16666…\\\\ \text{Mean}&=9.17\\\\ \end{aligned}$

1, \, 15, \, 2, \, 1, \, 17, \, 0

1, \, 4, \, 7, \, 1, \, 10, \, 15

5, \, 6, \, 9, \, 6, \, 2, \, 5

4, \, 8, \, 2, \, 9, \, 4, \, 5

Since each of the given data sets have $6$ data points, the total of the data points will be $6 \times 6$ (the mean times the number of data points).

$\begin{aligned} & 1+15+2+1+17+0=36 \\\\ & \text { Mean }=\cfrac{36}{6} \\\\ & \text { Mean }=6 \end{aligned}$

5

6

7

8

The total of $4$ numbers is:

$\text{Total of 4 values}=\text{mean} \times \text{number of values}=9\times 4=36$

The total of $3$ numbers is:

$6+8+15=29$

The difference between the totals is:

$36-29=7$

The $4^{th}$ number is $7.$

12

14

13

15

The total of $4$ numbers is:

$\text{Total of 4 values}=\text{mean} \times \text{number of values}=12\times 6=72$

The total of $5$ numbers is:

$7+9+11+13+18=58$

The difference between the totals is:

$72-58=14$

The $6^{th}$ number is $14.$

Mean in math FAQs

Does the data set of a sample mean have to be positive numbers?

No, the context in which the sample was collected may include negative numbers. For example, temperatures or account balances.

What is a weighted mean?

Instead of counting all data points equally, the mean of a set is found by counting (or “weighing”) certain data points more than others.

What is the standard deviation?

A way to quantify the amount of variation around the mean within a data set or population.

What is the mean, median and mode in a normal distribution?

In a normal distribution, all the measures of center are the same and are exactly at the center value. Thinking about the data in percentages, $68\%$ of the points are within one standard deviation of the mean, median and mode.

What are other types of mean besides arithmetic?

Geometric mean and harmonic mean are two other types of means. These are both addressed in upper level mathematics.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.