GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
3D trigonometry Area Area of a circle Substitution RoundingThis topic is relevant for:

How To Calculate Volume
Here we will learn how to calculate the volume of three-dimensional shapes, including cubes, cuboids, prisms, cylinders, pyramids, cones and spheres.
There are also volume worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is volume?
The volume of a 3D shape is the amount of space there is inside the shape.
To calculate the volume of a shape in three dimensions, we can use the relevant volume formula.
The table below shows the formulae that we can use for some of the most common 3D shapes.
Cuboid
Prism
Cylinder
Pyramid
Cone
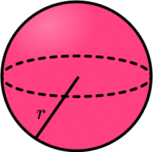
Sphere
\text{Volume }={h}\times{w}\times{h}
(\text{Volume }=
\text{Area of rectangle } \times \text{ Length})
\text{Volume }=
\text{Area of cross section} \times \text{ Length}
\text{Volume }=\pi{r}^2{h}
(\text{Volume }=
\text{Area of circle }\times\text{ Height})
\text{Volume }=
\frac{1}{3}\times\text{Area of base }\times\text{Height}
\text{Volume }=\frac{1}{3}\pi{r}^2{h}
\text{Volume }=
\frac{1}{3}\times\text{Area of base }\times\text{Height}
\text{Volume }=\frac{4}{3}\pi{r}^3
The formulae for the volume of a cone and the volume of a sphere are given to you for GCSE maths. You need to learn the other formulae.
Volume is measured in cubic units, including metric units such as cm^3 (cubic centimetres), m^3 (cubic metres) or mm^3 (cubic millimetres). Volume could also be measured in imperial units, including cubic feet or cubic inches. It can also be described using units of capacity such as millilitres, litres, pints or gallons.
Step-by-step guide: Volume formula
What is volume?

Volume of composite solid
You may be asked to calculate the volume of a 3 dimensional shape which is composed of 2 or more separate shapes. This type of shape is known as a composite shape. The volume of each of the shapes can be found and then added together.
For example,
Here is a composite shape. It is made of a cuboid and a pyramid.
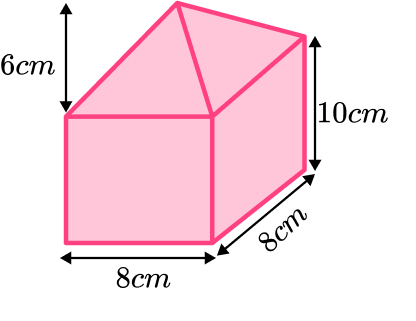
The volume of the cuboid is
8\times 8\times 10=640The volume of the pyramid is
\frac{1}{3} \times 8^2 \times 6=128The total volume can be found by adding the volume of the cuboid and the volume of the pyramid.
640+128=768 \ cm^3How to calculate volume
In order to calculate volume:
- Write down the formula.
- Substitute the values into the formula.
- Complete the calculation.
- Write the answer, including the units.
Explain how to calculate volume

Volume worksheet

Get your free volume worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Volume worksheet

Get your free volume worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEVolume examples
Example 1: volume of a cuboid
Calculate the volume of the cuboid below:
- Write down the formula.
The volume (V) of a cuboid is the same as the volume of a rectangular prism or the volume of a box.
\text{Volume } = {h}\times{w}\times{d}
2Substitute the values into the formula.
Given that h=3cm, \; w= 9cm, and d= 5cm, we have:
V = 3 \times 9 \times 5
3Complete the calculation.
V = 135
4Write the answer, including the units.
The dimensions of the cuboid are given in centimetres, so the volume will be in cubic centimetres (cm^3) .
V = 135cm^3
Step-by-step guide: Volume of a cuboid
Example 2: volume of a prism
Calculate the volume of this triangular prism:
Write down the formula.
\text{Volume of prism } = \text{Area of cross section} \times \text{Depth}
Substitute the values into the formula.
First, we need to find the area of the cross section, which is a triangle:
\begin{aligned} \text{Area of a triangle}&=\frac{1}{2}\times b \times h\\\\ &=\frac{1}{2}\times 2 \times 7\\\\ &=7\text{ m}^2 \end{aligned}
The depth of the prism is 6m, therefore:
\begin{aligned}
\text{Volume of prism }&= \text{Area of cross section} \times \text{ Depth}\\\\
&=7\times 6
\end{aligned}
Complete the calculation.
V = 42
Write the answer, including the units.
The dimensions are given in metres, so the volume is given in cubic metres (m^3):
V=42m^3
Step-by-step guide: Volume of a prism
Example 3: volume of a cylinder
Find the volume of the cylinder. Give your answer to 2 decimal places.
Write down the formula.
\text{Volume of a cylinder} = \pi r^{2}h
Substitute the values into the formula.
The height of the cylinder is 7cm and the radius is 5cm.
V=\pi \times 5^{2} \times 7
Complete the calculation.
V=\pi \times 5^{2} \times 7 = 549.7787144...
Write the answer, including the units.
V = 549.78cm^3
Step-by-step guide: Volume of a cylinder
Example 4: volume of a pyramid
Work out the volume of the pyramid:
Write down the formula.
\text{Volume of a pyramid} = \frac{1}{3} \times \text{ Area of base } \times \text{ Height}
Substitute the values into the formula.
First we need to find the area of the base
\begin{aligned} \text{Area of base }&=6 \times 6\\\\ &=36\text{cm}^2 \end{aligned}
\begin{aligned}
\text{Volume of pyramid }&=\frac{1}{3} \times \text{ Area of base } \times \text{ Height}\\\\
&=\frac{1}{3} \times 36 \times 7
\end{aligned}
Complete the calculation.
V = 84
Write the answer, including the units.
The length units are centimetres so the units for the volume are cubic centimetres (cm^3).
V=84cm^3
Step-by-step guide: Volume of a pyramid
Example 5: volume of a cone
Calculate the volume of the cone. Write your answer to 3 significant figures.
Write down the formula.
\text{Volume of a cone } = \frac{1}{3} \pi r^{2}h
Substitute the values into the formula.
The height of the cone is 6mm and the radius is 3mm.
V = \frac{1}{3} \times \pi \times 3^{2} \times 6
Complete the calculation.
V = \frac{1}{3} \times \pi \times 3^{2} \times 6 = 56.54866776...
Write the answer, including the units.
The dimensions are given in metres, so the volume is given in cubic millimetres (mm^3).
V=56.5mm^3
Step-by-step guide: Volume of a cone
Example 6: volume of a sphere
Work out the volume of the sphere. Give your answer to the nearest integer.
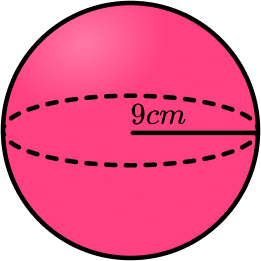
Write down the formula.
\text{Volume of a sphere } = \frac{4}{3} \pi r^{3}
Substitute the values into the formula.
The radius of the sphere is 9cm.
V=\frac{4}{3} \times \pi \times 9^{3}
Complete the calculation.
V = 3053.628059...
Write the answer, including the units.
V = 3054cm^3
Step-by-step guide: Volume of a sphere
Common misconceptions
- Missing/incorrect units
You should always include units in your answer.
Volume is measured in cubic units (e.g. mm^3, cm^3, m^3 etc)
- Calculating with different units
You need to make sure all measurements are in the same units before calculating the volume. (For example, you can’t have some measurements in cm and some in m ).
- Make sure you get the correct formula
Be careful to make sure you use the correct formula for the volume of the 3 D shape.
- Don’t round off too early
It is important to not round decimals until the end of the calculation. Rounding too early will result in an inaccurate answer.
Practice volume questions
1. Work out the volume of the cuboid
70cm^3

166cm^3

140cm^3

35cm^3

2. Calculate the volume of the prism.
300cm^3

420cm^3

320cm^3

210cm^3

3. Calculate the volume of the cylinder. Give your answer to 3 significant figures.
125m^3

314m^3

754m^3

628m^3

4. Find the volume of the pyramid
36cm^3

12cm^3

18cm^3

4cm^3

5. Find the volume of the cone. Give your answer to 1 d.p.
366.5mm^3

1099.6mm^3

146.6mm^3

70.0mm^3

6. Calculate the volume of the sphere. Give your answer to 3 s.f.
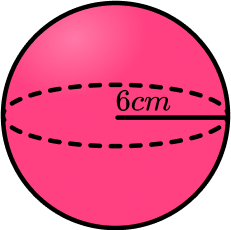
151cm^3

226cm^3

113cm^3

905cm^3

Volume GCSE questions
1. Calculate the volume of this cylinder. Give your answer to 1 decimal place.
(3 marks)
Radius = 5.5cm
(1)
\begin{aligned}
V&=\pi r^{2}h \\\\
&=\pi \times 5.5^{2} \times 7 \end{aligned}
(1)
\begin{aligned}
V&=665.2322444… \\\\
&=665.2\text{cm}^3
\end{aligned}
(1)
2. (a) Calculate the volume of this container
(b) Three spheres, each with radius 0.6m, are placed inside the container. What percentage of the space in the container do the spheres take up?
(5 marks)
(a)
\text{Area of cross-section: } \frac{1}{2}(1.4+2)\times 1.2=2.04
(1)
\text{Volume of prism: }2.04 \times 4 = 8.16\mathrm{m}^{3}
(1)
(b)
\text{Volume of one sphere: }\frac{4}{3} \times \pi \times 0.6^{3}=0.9048\mathrm{m}^{3}
(1)
\text{Total volume of three spheres: } 3 \times 0.9048=2.7144\mathrm{m}^{3}
(1)
\text{Percentage of space: }\frac{2.7144}{8.16} \times 100=33.3\%
(1)
3. Both of these cuboids have the same volume. Work out the height of cuboid B .
(4 marks)
\text{Volume of A: } 14 \times 6 \times 5=420\mathrm{cm}^{3}
(1)
\text{Volume of B: } 15 \times 7 \times h
(1)
\begin{aligned}
15 \times 7 \times{h}&=420\\\\
105h&=420
\end{aligned}
(1)
h=4cm
(1)
Learning checklist
You have now learned how to:
-
Calculate the volume of cuboids and prisms
-
Calculate the volume of cylinders, pyramids, cones and spheres
-
Use the properties of faces, surfaces, edges and vertices of cubes and cuboids to solve problems in 3D
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.