GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Operations involving decimal numbers Ratio ProportionThis topic is relevant for:
Exchange Rates
Here we will learn about how to work out exchange rates, including how to convert between British pounds and foreign currencies and read conversion graphs.
There are also how to work out exchange rate worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is an exchange rate?
An exchange rate is the rate at which the money of one country can be exchanged for the money of another country. It can also be referred to as a foreign exchange rate and be seen as the price of one currency expressed in terms of another currency.
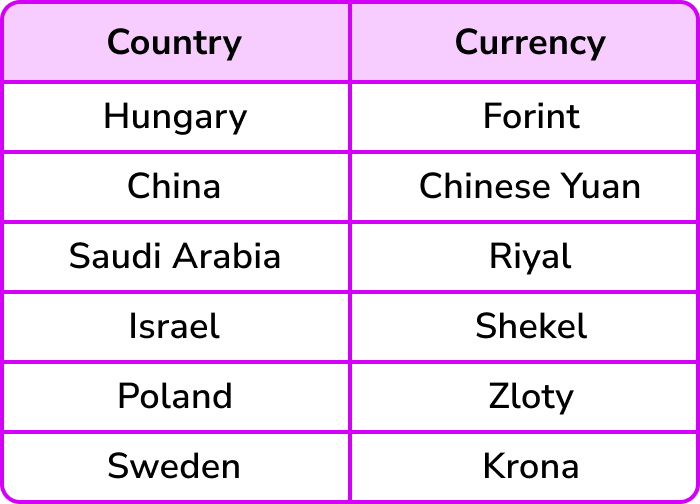
In the United Kingdom our currency is the British pound or pound sterling. The exchange rate tells us the value of £1 in terms of a foreign country’s currency. Different countries have different currencies.
For example,
The exchange rates are constantly changing depending on the country’s economic status. It is the role of the central bank to monitor these fluctuations and adjust the country’s monetary policy accordingly.
Using the exchange rate we can convert between pounds and foreign currencies. To do this we need to either multiply or divide the quantity we are trying to convert with the exchange rate.
To convert from British pounds to a foreign currency you must multiply by the exchange rate.
For example,
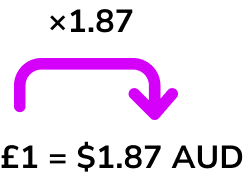
So £150 would be \$276 because 150 \times 1.87=276.
For example,
To convert from a foreign currency into British pounds you must divide by the exchange rate.
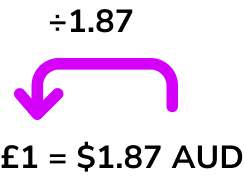
So, \$430 would be £229.95 because 430 \div 1.87=229.95 (to 2 dp).
A GCSE Mathematics question may ask you to convert between other currencies. It will normally give the exchange rate in a form similar to a 1:n ratio.
E.g.
Dollars to Euros
\$1 = €0.92To convert from the currency given as “1” we would multiply by the exchange rate.
To convert to the currency given as “1” we would divide by the exchange rate.
What is an exchange rate?
How to work out exchange rates
In order to convert currencies using exchange rates:
- Write down the exchange rate and the other information given. Keep the same currencies in line.
- Highlight the rate.
- Decide whether to multiply or divide by the rate.
If you are going from the “1” to the other currency then multiply.
If you are going to the “1” from the other currency then divide. - Multiply or divide the given currency by the exchange rate.
- State your final answer with the correct currency symbol.
Explain how to work out exchange rates
How to work out exchange rates worksheet
Get your free how to work out exchange rates worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE How to work out exchange rates worksheet
Get your free how to work out exchange rates worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEHow to work out exchange rates examples
Example 1: converting from pounds to a foreign currency
Given the exchange rate between pound and Australian dollars is £1 = \$1.87 , convert £70 to Australian dollars.
- Write down the exchange rate and the other information given. Keep the same currencies in line.
In the question we are given,
\begin{aligned} &£1 = \$1.87 \\\\ &£70^* \end{aligned}*Make sure to line up the £1 and £70 as they are the same currency.
2Highlight the rate.
\begin{aligned} & £1 = \colorbox{yellow}{$\$1.87^{*}$} \\\\ &£70 \end{aligned}*This tells us that every £1 is equal to \$1.87.
3Decide whether to multiply or divide by the rate.
If you are going from the “1” to the other currency then multiply.
If you are going to the “1” from the other currency then divide.
In this case we are going from pounds to Australian dollars so we need to multiply.
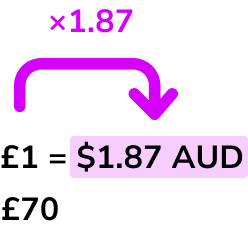
4Multiply or divide the given currency by the exchange rate.
Based on Step 3 , we need to multiply £70 by the rate which is \$1.87.
70 \times 1.87=130.905State your final answer with the correct currency symbol.
\colorbox{yellow}{$\bf{\$130.90} \textbf{ (Australian dollars)}$}Example 2: converting from a foreign currency into pounds
Sally just came back from a visit to the Philippines. In her purse she still had ₱135 (peso) which she wanted to convert back into pounds. A quick check on her foreign exchange app told her the current exchange rate was £1 = ₱69. How many pounds will she get?
Write down the exchange rate and the other information given. Keep the same currencies in line.
In the question we are given,
\begin{aligned} £1 = \ &₱69 \\\\ &₱135^* \end{aligned}
*Make sure to line up the £1 and ₱135 as they are the same currency.
Highlight the rate.
*This tells us that every £1 is equal to ₱69.
Decide whether to multiply or divide by the rate.
If you are going from the “1” to the other currency then multiply.
If you are going to the “1” from the other currency then divide.
In this case we are going from pesos to pound sterling so we need to divide.
Multiply or divide the given currency by the exchange rate.
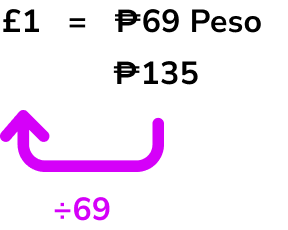
Based on Step 3 , we need to divide ₱135 by the rate which is ₱69.
135 \div 69=1.9565...
State your final answer with the correct currency symbol.
Example 3: comparing different currencies
In the USA a computer costs \$790. The same mobile phone costs £575 in the UK. Given that the current exchange rate is £1 = 1.35 \ USD, where is the mobile phone cheaper?
Write down the exchange rate and the other information given. Keep the same currencies in line.
In the question we are given,
£1 = \$1.35 \ USD
We are also asked to compare £575 and \$790. To compare them, we must convert them to the same currency. In this case, we can choose to either convert £575 into US dollars or \$790 into great British pounds (GBP).
For the purposes of this question, we will convert £575 to American dollars.
\begin{aligned} & £1 = \$1.35 \\\\ &£575^* \end{aligned}
*Make sure to line up the £1 and £575 as they are the same currency.
Highlight the rate.
*This tells us that every £1 is equal to \$1.35.
Decide whether to multiply or divide by the rate.
If you are going from the “1” to the other currency then multiply.
If you are going to the “1” from the other currency then divide.
In this case we are going from American dollars to British pounds so we need to multiply.
Multiply or divide the given currency by the exchange rate.
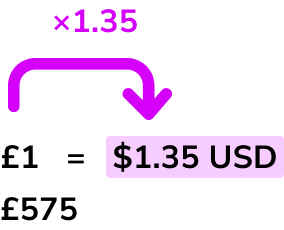
Based on Step 3 , we need to multiply \$575 by the rate which is \$1.35.
575 \times 1.35=776.25
State your final answer with the correct currency symbol.
The computer costs \$776.25 in England and \$790 in the United States.
Therefore, it is cheaper to buy the computer in the UK.
Example 4: worded question
Bonnie is flying home from Spain. She buys some food and drink on the plane.
| Price List |
| Crisps £2.50 |
| Chocolate Bar £1.75 |
| Pretzels £1.50 |
| Bottled water £3.70 |
| Tea £2 |
| Juice £1.80 |
Bonnie buys 2 chocolate bars, 2 pretzels and a bottle of water. The exchange rate is £1 = €1.17 (euros). She decided to use her leftover euros from her holiday to pay for her bill. Work out the cost of her bill in euros.
Write down the exchange rate and the other information given. Keep the same currencies in line.
In the question we are given,
£1 = €1.17 \ euros
We are also told that Bonnie buys 2 chocolate bars, 2 pretzels and a bottle of water.
We need to add together the cost of these items.
Total cost = 2 chocolate bars + \ 2 pretzels + \ 1 bottle of water
\begin{aligned} &=(2 \times 1.75)+(2 \times 1.50)+3.70 \\\\ &=£10.20 \end{aligned}
Since this total is in pounds we can put it under the pounds side of the exchange rate.
\begin{aligned} &£1 = €1.17 \\\\ &£10.20 \end{aligned}
Highlight the rate.
*This tells us that every £1 is equal to €1.17.
Decide whether to multiply or divide by the rate.
If you are going from the “1” to the other currency then multiply.
If you are going to the “1” from the other currency then divide.
In this case we are going from pound sterling to euros so we need to multiply.
Multiply or divide the given currency by the exchange rate.
Based on Step 3 , we need to multiply £10.20 by the rate which is €1.17.
10.20 \times 1.17=11.93
State your final answer with the correct currency symbol.
The total cost of her bill in euros is \colorbox{yellow}{$ €11.93.$}
Example 5: worded question
Samantha is planning a holiday to Turkey.
She needs to exchange some of her British pounds into Turkish lira.
The bank only stock ₺100 notes.
Samantha only wants to exchange up to £550 into Turkish lira.
She wants to get as many ₺100 notes as possible.
The current exchange rate is £1=₺12.81.
How many ₺100 notes should she get?
Write down the exchange rate and the other information given. Keep the same currencies in line.
In the question we are given,
\begin{aligned} &£1=₺12.81 \\\\ &£550^* \end{aligned}
*Make sure to line up the £1 and £550 as they are the same currency.
Highlight the rate.
*This tells us that every £1 is equal to ₺12.81.
Decide whether to multiply or divide by the rate.
If you are going from the “1” to the other currency then multiply.
If you are going to the “1” from the other currency then divide.
In this case we are going from pounds to Turkish lira so we need to multiply.
Multiply or divide the given currency by the exchange rate.
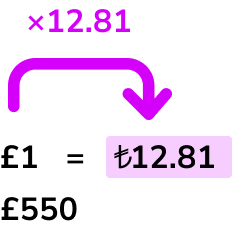
Based on Step 3 , we need to multiply £550 by the rate which is ₺12.81.
550 \times 12.81=6655
State your final answer with the correct currency symbol.
Samantha would get ₺6655 if she converted £550. The bank only stock ₺100 notes so we need to divide ₺6655 by 100 to see how many notes she would get.
This would give us ₺66.55. Since you cannot get 0.55 of a note, this value can be rounded to 66.
She would get \colorbox{yellow}{$\bf{66 \ ₺100} $} notes.
Example 6: conversion graphs
Use the graph below to answer the following questions.
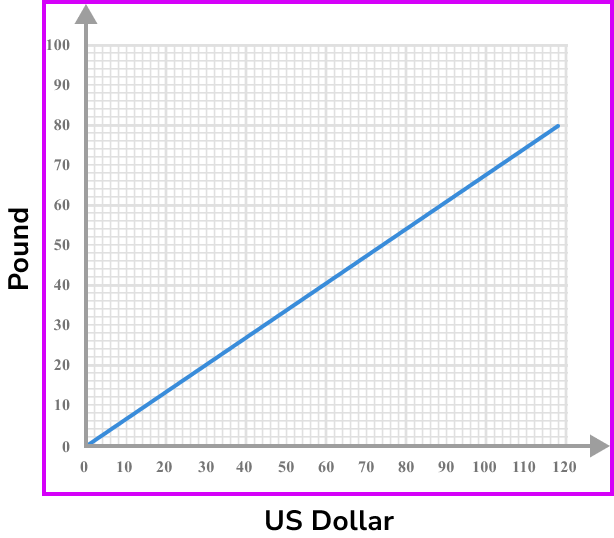
a) Change \$30 USD to pounds.
b) Change £65 to US dollars.
c) Change £100 to US dollars.
a Change \bf{\$30} USD to pounds.
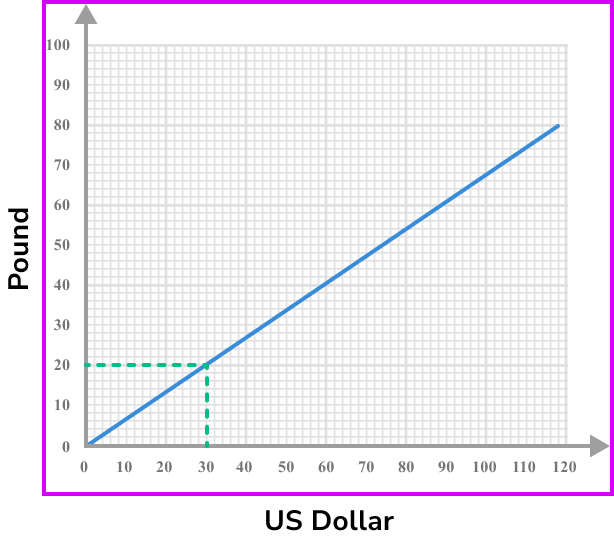
Draw a line going up from \$30 until you hit the line, then look across to the vertical axis and read the value.
In this case \$30 = £20.
b Change \bf{£65} to US dollars.
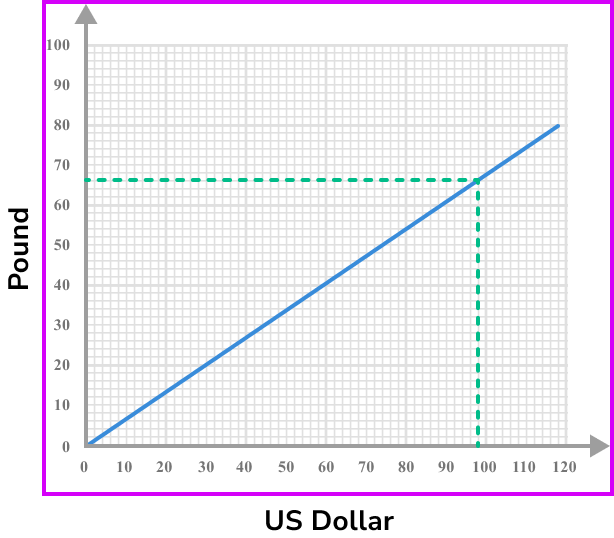
Draw a line going across £65 until you hit the line, then look down to the horizontal axis and read the value.
In this case £65 = \$96 USD.
c Change \bf{£100} to US dollars.
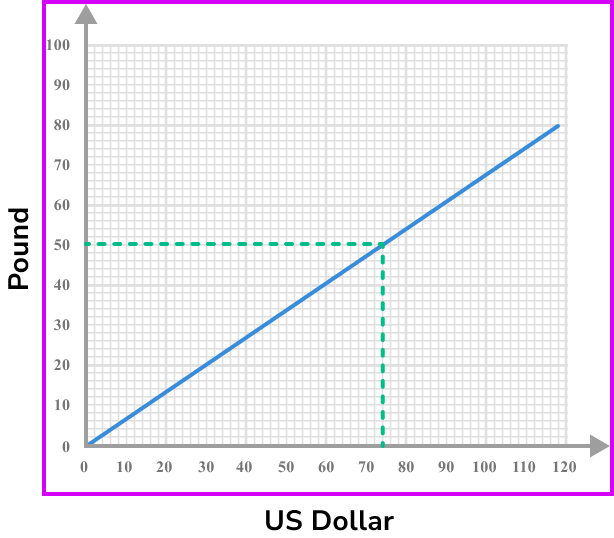
Since the graph does not extend to £100, we need to use the values that we know and use them to calculate how many USD £100 is equal to.
Draw a line going across from \$50 USD to the line and down to \$74.
Since we know that
£50 = \$74 .
If we multiply both sides by 2 we get
£100 = \$148 USD.
Step-by-step guide: Conversion graphs
Common misconceptions
- Multiply or divide by the exchange rate
Pupils may get confused whether they need to multiply or divide by the exchange rate. Remember, If you are going from the “1” to the other currency then multiply. If you are going to the “1” from the other currency then divide.
- Lining up the same currencies together
When given information in the question be careful to check what currency the values are in and line up accordingly. If you mix up the currencies it will be difficult to know whether to multiply or divide by the exchange rate.
- Rounding
When rounding, it is usual that we need to round to 2 decimal places. For example, if calculating British pounds we get 231.7851, the final answer would be £217.79. The 2 decimal places would be the pence.
Practice how to work out exchange rates questions
1. Given the exchange rate between British pounds and New Zealand dollars is £1 = \$1.95, convert £90 to New Zealand dollars.
Multiply £90 by the exchange rate 1.95.
90\times 1.95=175.5
This would be £175.70 .
2. Given the exchange rate between British pounds and the Indian rupee is £1 = ₹103.10, convert ₹5000 to pound sterling.
Divide ₹5000 by the exchange rate 103.10.
5000\div 103.10=48.4966…
This would be £48.50 to the nearest pence.
3. In China an iPad costs ¥2500 (Chinese Yuan). The same iPad costs £300 in the UK. Given that the current exchange rate is £1 = ¥8.85, where is the iPad cheaper?
The UK by ¥155
China by ¥2200
China by ¥155
The price is the same in both countries
Convert £300 into Chinese Yuan by multiplying by 8.85.
300\times 8.85=2655
This would be more expensive than the price in China by ¥155.
4. Lucy is buying some items from an online shop which will accept payments in Pounds and Euros.
She buys: a watch costing £150
a pendant costing £280
a frame costing £17
The exchange rate is £1 = €1.27. Work out the cost of her bill in Euros.
Add up the prices.
\pounds 150 + \pounds 280+ \pounds 17=\pounds 447
Multiply the total by the exchange rate 1.27.
447\times 1.27=567.69
This gives €567.69 .
5. Sangita is planning a holiday to Thailand.
She needs to exchange some of her British pounds into Thai Bahts.
The bank only stock ฿1000 notes.
Sangita only wants to exchange up to £100 into Thai baht.
She wants to get as many ฿1000 notes as possible.
The current exchange rate is £1=฿45.95.
How many ฿1000 notes should she get?
Multiply =£100 by 45.95, then divide by 1000 to determine how many notes she should get.
100\times 45.95=4595
This gives ฿4595.
We then need to work out the number of ฿1000 notes.
4595\div 1000=4.595
So Sangits would be able to get 4 \ ฿1000 notes.
How to work out exchange rates GCSE questions
1. Samantha goes on holiday to Japan.
She exchanged £850 into Japanese yen.
The exchange rate was £1 = JP¥156.88 .
(a) Change £850 into Japanese yen.
(b) When she returned she had JP¥180 left which she wanted to exchange back into pounds.
She checked the currency exchange rates app on her phone and found that the new rate was £1 = JP¥157.22.
Change JP¥180 into British pounds.
(4 marks)
(a)
850 \times 156.88
(1)
JP¥133348(1)
(b)
180 \div 157.22
(1)
£1.14(1)
2. (a) On a flight back to London from Hong Kong, Jackie purchased the following items from the in-flight dining options.
- A blueberry muffin costing £2.50
- A diet coke costing £3.50
- A tuna sandwich costing £5.50
She paid part of the bill with the HK\$60 left from her holiday and paid the rest in British pounds.
The exchange rate between the British pound and the Hong Kong dollar is £1= HK\$10.68.
How much does Jackie pay in British pounds?
(b) When paying the bill Jackie realised that there was a 10\% service charge on her bill.
What was her total bill in Hong Kong dollars (HKD)? Give your answer to the nearest Hong Kong dollar.
(6 marks)
(a)
2.50+3.50+5.50=£11.50
(1)
60 \div 10.68=£5.62(1)
11.50-5.62 = £5.88(1)
(b)
11.50 \times 1.10=£12.65
(1)
£12.65 \times 10.68=135.102(1)
HK\$135(1)
3. Paula goes on holiday to Canada.
She exchanged £550 into Canadian dollars.
The exchange rate was £1 = \$1.70 .
(a) Change £550 into Canadian dollars.
(b) While in Canada Paula noticed a blazer she really liked. The blazer cost \$132 \ CDN. She had seen the exact same blazer in England for £79.
Using the same exchange rate as (a), determine where the blazer is cheaper and by how much.
(5 marks)
(a)
550 \times 1.70(1)
\$935(1)
(b)
79 \times 1.70=\$134.30(1)
134.30-132=\$2.30(1)
The blazer is cheaper in Canada by \$2.30 .
(1)
Alternatively
132\div 1.70= \pounds 77.65
(1)
79-77.65=£1.35(1)
The blazer is cheaper in Canada by £1.35 .
(1)
Learning checklist
You have now learned how to:
- Convert between related units (prices, currencies) in numerical contexts
- Interpret graphs that illustrate direct proportion, such as currencies
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.
Find out more about our GCSE maths tuition programme.