Sin cos tan

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Angles in a triangle Rearranging equations Pythagoras theorem

This topic is relevant for:

GCSE Maths Geometry and Measure Trigonometry Trig Formula

Sin Cos Tan

Here we will learn about sin cos tan, including understanding what these three trigonometric functions are and their ratios, understanding when to use these functions and their inverse, and how to use them.

There are also sin cos tan worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is sin cos tan?

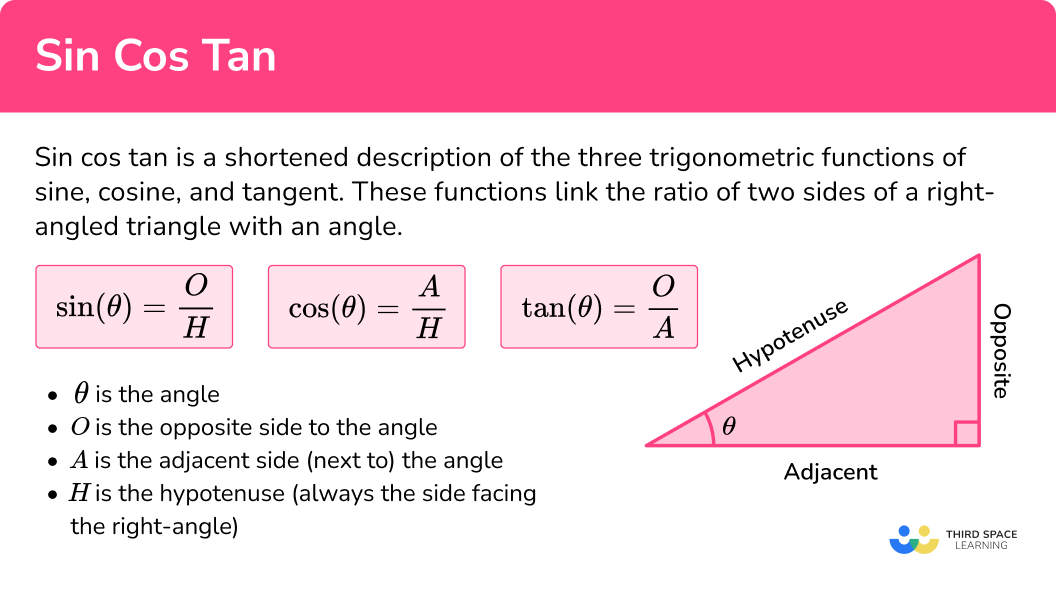
Sin cos tan is a shortened description of the three trigonometric functions of sine, cosine, and tangent. These functions associate the ratio of two sides of a right-angled triangle with an angle.

To calculate using sin, cos and tan, we need to know their trigonometric ratios (remember that the ratio of two values is a division of these values). Consider the right-angled triangle below.

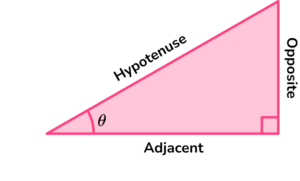
$\theta$ is the angle.
The opposite side $\textbf{(O)}$ is opposite to the angle.
The adjacent side $\textbf{(A)}$ is next to the angle.
The hypotenuse $\textbf{(H)}$ is the longest side (always the side facing the right-angle).

The three trigonometric ratios can be used to determine a missing side or a missing angle. We use the following trigonometric formulae.

Sine	Cosine	Tangent

$\sin{\theta}=\frac{O}{H}$	$\cos{\theta}=\frac{A}{H}$	$\tan{\theta}=\frac{O}{A}$

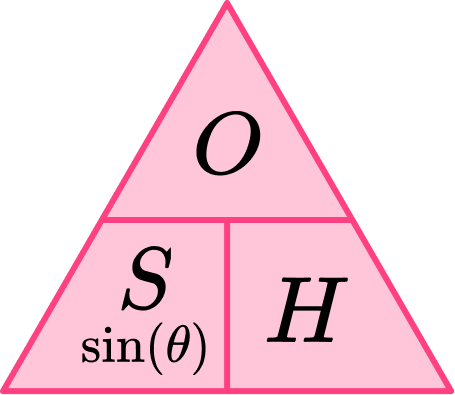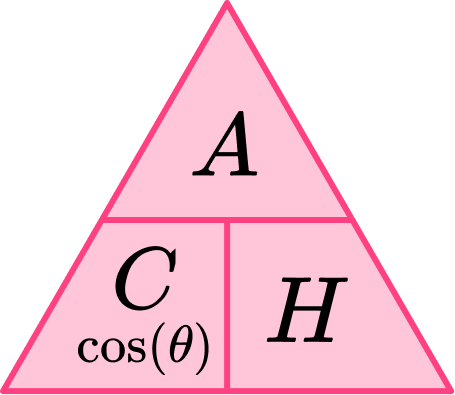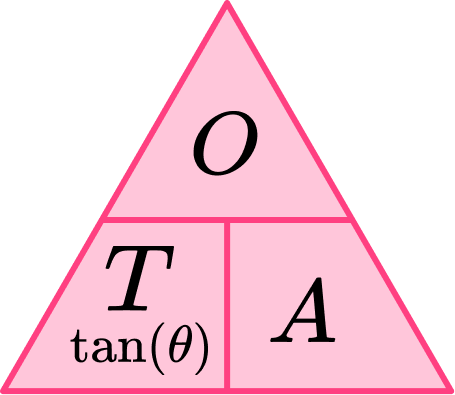If we look at the letters only within the three triangles above, we get the abbreviation SOHCAHTOA where

SOH is the association of the sine of an angle $\text{(S)}$ with the opposite side $\text{(O)}$ and the hypotenuse $\text{(H)}$ of the triangle.
CAH is the association of the cosine of an angle $\text{(C)}$ with the adjacent side $\text{(A)}$ and the hypotenuse $\text{(H)}$ of the triangle.
TOA is the association of the tangent of an angle $\text{(T)}$ with the opposite side $\text{(O)}$ and the adjacent side $\text{(A)}$ of the triangle.

Step-by-step guide: SOHCAHTOA

Step-by-step guide: Area of a triangle trig

We use one of the three trigonometric ratios of $\textbf{sin θ}, \ \textbf{cos θ},$ and $\textbf{tan θ}$ to find one of the missing sides of a right angled triangle when we know another angle, apart from the right-angle.

We use the inverse functions of the three trigonometric ratios to determine a missing angle $\theta$ (pronounced theta).

The inverse sine function is written as $\theta=\sin^{-1}\left(\frac{O}{H}\right).$
The inverse cosine function is written as $\theta=\cos^{-1}\left(\frac{A}{H}\right).$
The inverse tangent function is written as $\theta=\tan^{-1}\left(\frac{O}{A}\right).$

Step-by-step guide: Trigonometric functions

Step-by-step guide: Cosine rule

Step-by-step guide: Sine rule

What is sin cos tan?

How to calculate using sin cos tan

In order to calculate using sin cos tan:

Label the sides of the right-angled triangle that we have information about in relation to the angle $\textbf{θ}$ .
Choose the trig ratio we need.
Substitute the values from the triangle into the function.
Calculate the unknown side or angle, rearranging if necessary.

See also: Trigonometry formula

See also: Trig identities

Explain how to calculate using sin cos tan

SOHCAHTOA worksheet (includes sin cos tan)

Get your free sin cos tan worksheet of 20+ SOHCAHTOA questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

SOHCAHTOA worksheet (includes sin cos tan)

Get your free sin cos tan worksheet of 20+ SOHCAHTOA questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Sin cos tan examples

Example 1: missing side (sine)

Determine the length of the hypotenuse for the triangle $\text{ABC}$ below.

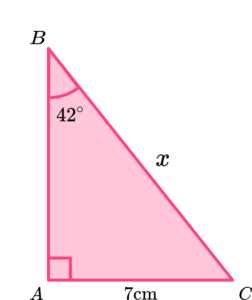
Label the sides of the right-angled triangle that we have information about in relation to the angle $\textbf{θ}$ .

Labelling the sides in relation to the angle, we have,

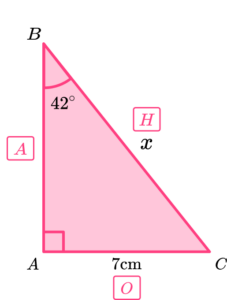
2Choose the trig ratio we need.

We know that $\ \theta=42^{\circ}, \ O=7$ and $H=x.$ Using SOHCAHTOA, we can use the sine ratio (SOH) to determine the missing length of the hypotenuse.

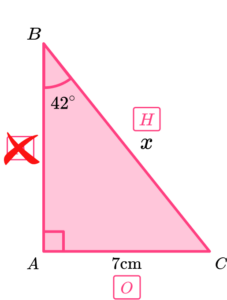
3Substitute the values from the triangle into the function.

Substituting these values into the trigonometry formula $\sin \theta=\frac{O}{H},$ we have

\sin{42}=\frac{7}{x}.

4Calculate the unknown side or angle, rearranging if necessary.

We need $x$ to be the subject of the formula and so we first have to multiply both sides by $x$ to get

x\times\sin{42}=7.

Dividing both sides of the equation by $\sin 42,$ we get

x=\frac{7}{\sin{42}}=10.46133585…

The length of the hypotenuse $x=10.46 \ cm\text{ (2dp).}$

Example 2: missing side (cosine)

Determine the length of the adjacent side for the triangle $\text{PQR}$ below.

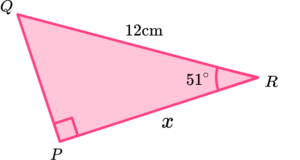
Label the sides of the right-angled triangle that we have information about in relation to the angle $\textbf{θ}$ .

Labelling the sides in relation to the angle, we have,

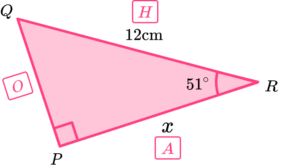
Choose the trig ratio we need.

We know that $\ \theta=51^{\circ}, \ A=x$ and $H=12.$ Using SOHCAHTOA, we can use the cosine ratio (CAH) to determine the missing length of the adjacent side.

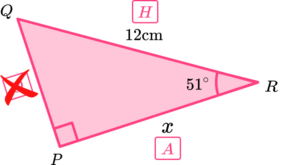
Substitute the values from the triangle into the function.

Substituting these values into the trigonometry formula $\cos\theta=\frac{A}{H},$ we have

$\cos{51}=\frac{x}{12}.$

Calculate the unknown side or angle, rearranging if necessary.

We need $x$ to be the subject of the formula and so we need to multiply both sides by $12$ to get

$12\times\cos{51}=x.$

$x=12\cos{51}=7.551844693…$

The length of the adjacent side $x=7.55 \ cm\text{ (2dp).}$

Example 3: missing side (tangent)

Determine the length of the adjacent side for the triangle $\text{EFG}$ below.

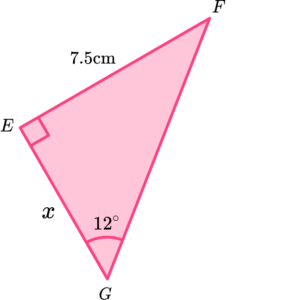
Label the sides of the right-angled triangle that we have information about in relation to the angle $\textbf{θ}$ .

Labelling the sides in relation to the angle, we have,

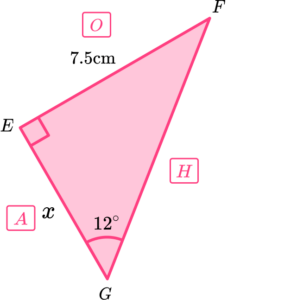
Choose the trig ratio we need.

We know that $\ \theta=12^{\circ}, \ O=7.5$ and $A=x.$ Using SOHCAHTOA, we can use the tangent ratio (TOA) to determine the missing length of the adjacent side.

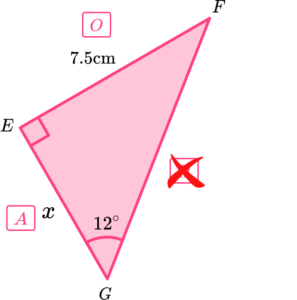
Substitute the values from the triangle into the function.

Substituting these values into the trigonometry formula $\tan\theta=\frac{O}{A},$ we have

$\tan{12}=\frac{7.5}{x}.$

Calculate the unknown side or angle, rearranging if necessary.

We need $x$ to be the subject of the formula and so we first have to multiply both sides by $x$ to get

$x\times\tan{12}=7.5.$

Dividing both sides of the equation by $\tan 12,$ we get

$x=\frac{7.5}{\tan{12}}=35.28472582…$

The length of the adjacent side $x=35.28 \ cm\text{ (2dp).}$

Example 4: missing angle (sine)

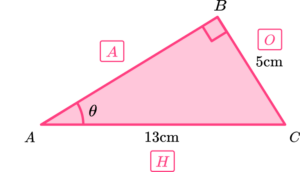
Determine the size of the angle $\theta$ for the triangle $\text{ABC}$ below.

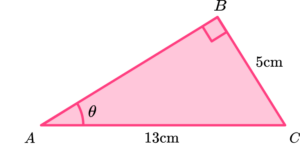
Label the sides of the right-angled triangle that we have information about in relation to the angle $\textbf{θ}$ .

Labelling the sides in relation to the angle, we have,

Choose the trig ratio we need.

We know that $\ O=5, \ H=13$ and we want to find the angle $\theta.$ Using SOHCAHTOA, we can use the sine ratio (SOH) however we need to use the inverse sine function as we need to calculate the angle.

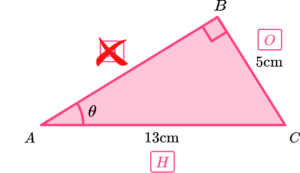
Substitute the values from the triangle into the function.

Substituting these values into the trigonometry formula $\sin\theta=\frac{O}{H},$ we have

$\sin{\theta}=\frac{5}{13}.$

This rearranges to

$\theta=\sin^{-1}\left(\frac{5}{13}\right).$

Calculate the unknown side or angle, rearranging if necessary.

Using a calculator, we can simply input this to determine the angle.

$\theta=22.61986495…$

The angle $\theta=22.6^{\circ}\text{ (1dp).}$

Example 5: missing angle (cosine)

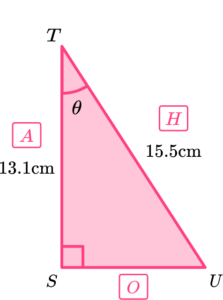
Determine the size of the angle $\theta$ for the triangle $\text{STU}$ below.

Label the sides of the right-angled triangle that we have information about in relation to the angle $\textbf{θ}$ .

Labelling the sides in relation to the angle, we have,

Choose the trig ratio we need.

We know that $\ A=13.1, \ H=15.5$ and we want to find the angle $\theta.$ Using SOHCAHTOA, we can use the cosine ratio (CAH) however we need to use the inverse cosine function as we need to calculate the angle.

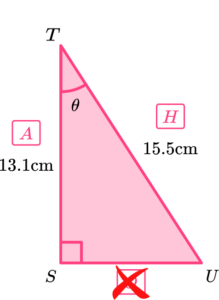
Substitute the values from the triangle into the function.

Substituting these values into the trigonometry formula $\cos\theta=\frac{A}{H},$ we have

$\cos{\theta}=\frac{13.1}{15.5}.$

This rearranges to

$\theta=\cos^{-1}\left(\frac{13.1}{15.5}\right).$

Calculate the unknown side or angle, rearranging if necessary.

Using a calculator, we can simply input this to determine the angle.

$\theta=32.31077908…$

The angle $\theta=32.3^{\circ}\text{ (1dp).}$

Example 6: missing angle (tangent)

Determine the size of the angle $\theta$ for the triangle $\text{XYZ}$ below.

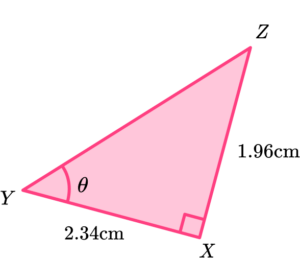
Label the sides of the right-angled triangle that we have information about in relation to the angle $\textbf{θ}$ .

Labelling the sides in relation to the angle, we have,

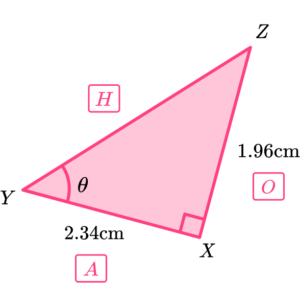
Choose the trig ratio we need.

We know that $\ O=1.96, \ A=2.34$ and we want to find the angle $\theta.$ Using SOHCAHTOA, we can use the tangent ratio (TOA) however we need to use the inverse tangent function as we need to calculate the angle.

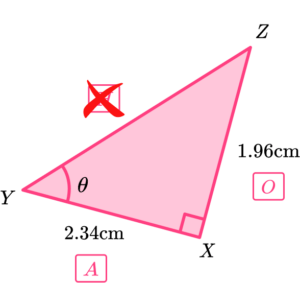
Substitute the values from the triangle into the function.

Substituting these values into the trigonometry formula $\tan\theta=\frac{O}{A},$ we have

$\tan{\theta}=\frac{1.96}{2.34}.$

This rearranges to

$\theta=\tan^{-1}\left(\frac{1.96}{2.34}\right).$

Calculate the unknown side or angle, rearranging if necessary.

Using a calculator, we can simply input this to determine the angle.

$\theta=39.94977158…$

The angle $\theta=39.9^{\circ}\text{ (1dp).}$

Common misconceptions

Make sure your calculator is set to degrees

All angles at GCSE are measured in degrees. Make sure your calculator screen is showing a small ‘D’ at the top before using it for trigonometry. If it is showing an ‘R’ it will measure the angle in radians which are not needed until A Level.

Right triangle

Right-angled triangles are sometimes called right triangles.

When to use SOHCAHTOA

We can use SOHCAHTOA to find a missing side of a right-angled triangle when we have another side and a given angle.

We can use SOHCAHTOA to find a missing angle of a right-angled triangle when we have two given sides.

If we have two sides and we want to find the third we can use the Pythagorean theorem $a^{2}+b^{2}=c^{2}.$

Standard or inverse trig function

We use standard trig functions when we know the angle. We have to use the inverse trig functions when we don’t know the angle.

Practice sin cos tan questions

4.67 \ cm

6.02 \ cm

12.11 \ cm

13.45 \ cm

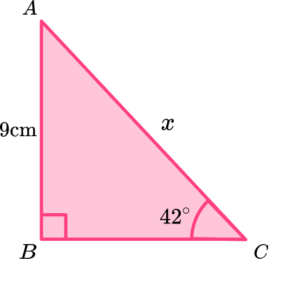
From the angle $\theta=42^{\circ}$ we know that $O=9$ and $H=x$ so we use the sine ratio,

\sin\theta=\frac{O}{H}.

\sin{42}=\frac{9}{x}

x=\frac{9}{\sin{42}}=13.45028895…=13.45 \ cm\text{ (2dp)}

20.90 \ cm

23.37 \ cm

64.18 \ cm

67.88 \ cm

From the angle $\theta=19^{\circ}$ we know that $A=22.1$ and $H=x$ so we use the cosine ratio,

\cos\theta=\frac{A}{H}.

\cos{19}=\frac{22.1}{x}

x=\frac{22.1}{\cos{19}}=23.37341705…=23.37 \ cm\text{ (2dp)}

28.8 \ cm

1.2 \ cm

0.1 \ cm

7.7 \ cm

From the angle $\theta=72^{\circ}$ we know that $O=x$ and $A=0.4$ so we use the tangent ratio,

\tan\theta=\frac{O}{A}.

\tan{72}=\frac{x}{0.4}

x=0.4\times\tan{72}=1.231073415…=1.2 \ cm\text{ (1dp)}

26.57^{\circ}\text{ (2dp)}

30^{\circ}

60^{\circ}

63.43^{\circ}\text{ (2dp)}

From the angle $\theta$ we know that $O=2.2$ and $H=4.4.$ As we need to find the angle, we use the inverse sine ratio,

\theta=\sin^{-1}\left(\frac{O}{H}\right).

\theta=\sin^{-1}\left(\frac{2.2}{4.4}\right)=30^{\circ}

9.4^{\circ}

9.6^{\circ}

48.4^{\circ}

80.4^{\circ}

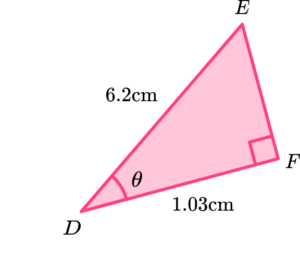
From the angle $\theta$ we know that $A=1.03$ and $H=6.2.$ As we need to find the angle, we use the inverse cosine ratio,

\theta=\cos^{-1}\left(\frac{A}{H}\right).

\theta=\cos^{-1}\left(\frac{1.03}{6.2}\right)=80.4^{\circ} \ (1dp)

43.18^{\circ}

20.21^{\circ}

69.79^{\circ}

46.82^{\circ}

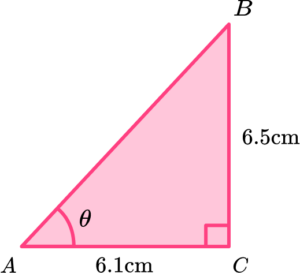
From the angle $\theta$ we know that $O=6.5$ and $A=6.1.$ As we need to find the angle, we use the inverse tangent ratio,

\theta=\tan^{-1}\left(\frac{O}{A}\right).

\theta=\tan^{-1}\left(\frac{6.5}{6.1}\right)=46.81830296…=46.82^{\circ}\text{ (2dp)}

Sin cos tan GCSE questions

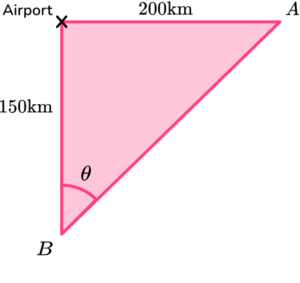
1. Two planes take off from the same airport travelling at the same speed. Plane $\text{A}$ flies East for $200 \ km.$ Plane $\text{B}$ flies South for $150 \ km.$

Determine the bearing of plane $\text{A}$ from plane $\text{B}$ at this time.

(3 marks)

Show answer

\tan\theta=\frac{200}{150}

(1)

\theta=\tan^{-1}\left(\frac{200}{150}\right)

(1)

=53.1^{\circ}

(1)

Diagram:

Sin cos tan GCSE question 1

2. Triangles $\text{ABC}$ and $\text{ACD}$ are joined along the side length $\text{AC}$ such that $\text{BCD}$ is a straight line. The length of $\text{BC:BD} = 1:4.$

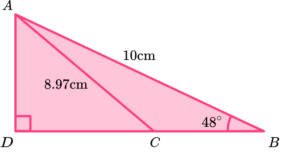
Sin cos tan GCSE question 2

(a) Determine the length of $\text{CD}$ to $3$ significant figures.

(b) Use your answer to part a) to determine the size of angle $\text{CAD}.$

(5 marks)

Show answer

(a)

BD=10\cos(48)=6.691…

(1)

CD=\frac{3}{4}\times{6.691…}

(1)

5.02 \ cm \text{ (3sf)}

(1)

Alternative method:

AD=10\sin(48)=7.4314…

(1)

CD=\sqrt{8.97^2-7.4313…^2}

(1)

5.02 \ cm \text{ (3sf)}

(1)

(b)

\theta=\sin^{-1}\left(\frac{5.02}{8.97}\right)

(1)

\theta=34.03^{\circ}

(1)

Alternative method:

\theta=\sin^{-1}\left(\frac{5.02}{8.97}\right)

(1)

\theta=34.06^{\circ}

(1)

Answer is range $\{34.03-34.06\}$

3. A man is standing $12.8 \ m$ from the wall of a block of flats, looking towards the top of the building at an angle of $76^{\circ}.$

The man is $1.8 \ m$ tall. Determine the height of the block of flats, labelled $x.$

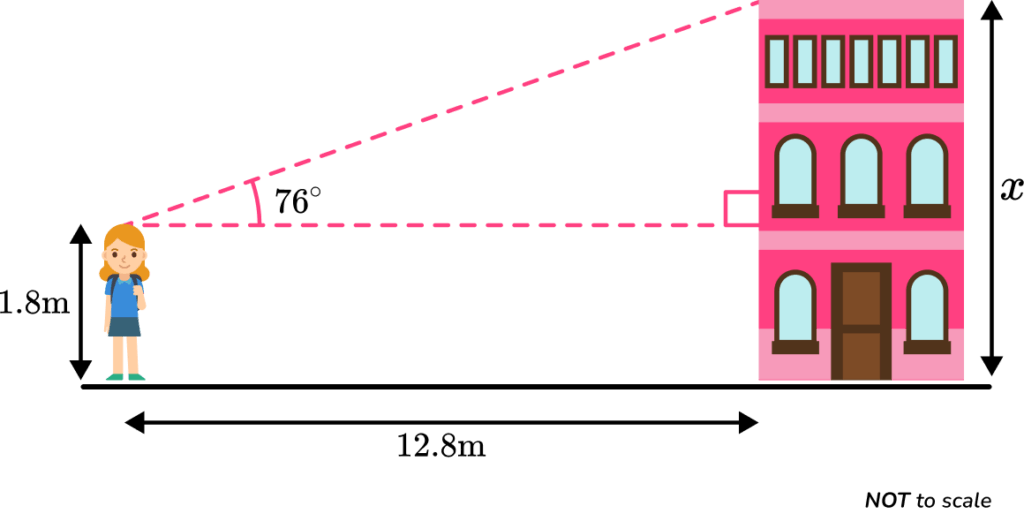
Sin cos tan GCSE question 3

(3 marks)

Show answer

\tan(76)=\frac{O}{12.8}

(1)

51.337\dots+1.8

(1)

x=52.1 \ m \text{ (3sf)}

(1)

Learning checklist

You have now learned how to:

Apply trigonometric ratios to find angles and lengths in right-angled triangles

The next lessons are

Beyond GCSE

At A Level, we continue to develop understanding beyond the basic trigonometry functions of sine, cosine, and tangent. New functions that are studied include,

The secant function $(\sec \theta)$ where $\frac{1}{\sin\theta}=\sec\theta.$
The cosecant function referred to as the cosec function $(\csc \theta)$ where $\frac{1}{\cos\theta}=\csc\theta.$
The cotangent function $(\cot \theta)$ where $\frac{1}{\tan\theta}=\cot\theta.$

We study the derivatives of trig functions and are introduced to another unit of measure for angles called radians.

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Introduction

What is sin cos tan?

How to calculate using sin cos tan

Sin cos tan worksheet

Sin cos tan examples

↓

Example 1: missing side (sine) Example 2: missing side (cosine) Example 3: missing side (tangent) Example 4: missing angle (sine) Example 5: missing angle (cosine) Example 6: missing angle (tangent)

Common misconceptions

Practice sin cos tan questions

Sin cos tan GCSE questions

Learning checklist

Next lessons

Beyond GCSE

Still stuck?