GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
This topic is relevant for:
Polygons
Here we will learn about polygons, including regular polygons, angles in polygons, and complex polygons.
There are also polygons worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is a polygon?
A polygon is a 2D shape with straight sides.
Two sides of a polygon meet at a vertex (plural vertices). A 2D polygon is a plane figure meaning that it is drawn on the flat, cartesian plane.
You need to be able to classify geometric shapes based on their properties and sides and find unknown angles in any triangle, quadrilateral and regular polygon. To do this, we need to look closely at the properties of these shapes.
Types of polygons
The table gives the names of various polygon with their number of sides
| Polygon | Number of Sides |
| Triangle | 3 |
| Quadrilateral | 4 |
| Pentagon | 5 |
| Hexagon | 6 |
| Heptagon | 7 |
| Octagon | 8 |
| Nonagon | 9 |
| Decagon | 10 |
| Hendecagon | 11 |
| Dodecagon | 12 |
| Heptadecagon | 17 |
| Icosagon | 20 |
| N-gon | n |
What is a polygon?
How to use polygons
There are various ways of using polygons, these are summarised below.
1. Regular polygons
Regular polygons have specific properties, they have equal side lengths and equal internal angles.
Equilateral triangle
Square
Regular pentagon
Step-by-step guide: Regular polygons
2. Irregular polygons
Irregular polygons do not have equal sides and do not have equal angles. When the number of sides is unknown, we describe this shape as an n-gon where the number of sides is given as n .
Trapezium
Irregular pentagon
Irregular dodecagon
Step-by-step guide: Irregular polygons
3. Types of triangle
There are 5 different types of triangle.
Properties of triangles are very important within geometry. They are one of the most common shapes to recognise for angles in parallel lines, circle theorems, interior angles, trigonometry, Pythagoras theorem, and many more. You therefore must be familiar with their individual properties.
Step-by-step guide: Triangles
4. Types of quadrilaterals
Quadrilaterals are four sided shapes (quad meaning four, lateral meaning lines).
There are many different types of quadrilaterals and you should be able to recall (or calculate) the properties for each polygon.
Step-by-step guide: Types of quadrilaterals
5. Angles in polygons
In order to determine whether a polygon is regular, a specific type of polygon (for example, a rhombus or an isosceles triangle) or to determine how many sides a polygon has, angles are the most important property to look at. We need to be familiar with interior and exterior angles.
- Interior angles are angles that are contained within the polygon. Regular polygons have equal interior angles as this property along with equal side lengths make them regular.
Regular Hexagon
Regular Pentagon
The sum of interior angles can be calculated using the formula:
Sum of interior angles = (n-2) \times 180
where n represents the number of sides.
- Exterior angles are supplementary to the interior angle, where the sum of the interior and exterior angle equal 180^{\circ} . We can use this property to find either the interior angle, or exterior angle at a vertex.
The sum of exterior angles is always 360^{\circ}.
For any polygon,
Sum of exterior angles of a polygon = 360^{\circ} .
Regular Hexagon
Regular Pentagon
Step-by-step guide: Hexagon shape
See also: Interior angles
See also: Exterior angles
6. Convex and concave polygons
A convex polygon is a polygon with all the interior angles less than 180^{\circ} . A concave polygon has at least one angle that is greater than 180^{\circ} (or a reflex angle).
For example,
Convex hexagon
All interior angles are
either acute or obtuse.
Concave hexagon
At least one angle is
greater than 180^o.
The minimum number of edges of a polygon for it to be able to be concave is four (specifically an arrowhead).
7. Simple and complex polygons
A simple polygon is an isolated shape that can be viewed as one single object.
A complex polygon has overlapping or shared edges and so the polygon can be broken down into smaller polygons.
For example,
An example of a complex polygon is the pentagram or five pointed star.
The pentagram has ten vertices; the five vertices of the star, and the five vertices of the inner pentagon. Although the shape has 10 vertices and 10 outer edges, we cannot describe this polygon as a decagon because the pentagram is made up of fifteen line segments, not 10.
Other types of complex polygons include other n-pointed stars (heptagram, decagram, octagram), the antiparallelogram, and nets of 3D shapes.
Antiparallelogram
Octagram
How to classify a polygon
In order to classify a polygon:
- State/calculate the number of sides of the polygon.
- Determine the size of the angles/side lengths within the polygon.
- Recognise the other properties of the polygon.
How to classify a polygon
Polygons worksheet
Get your free polygons worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONPolygons worksheet
Get your free polygons worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONPolygons examples
Example 1: triangle
Correctly classify the following polygon.
- State/calculate the number of sides of the polygon.
The polygon has three sides so we are looking at a triangle.
2Determine the size of the angles/side lengths within the polygon.
Angles in a triangle total 180^{\circ} and so the missing angle is equal to 180 - (70+55)=55^{\circ} .
3Recognise the other properties of the polygon.
As two angles are the same length, the missing side must be equal to 7cm. The triangle also has one line of symmetry (vertical) and no rotational symmetry.
The polygon is an isosceles triangle.
Example 2: quadrilateral
Determine what type of quadrilateral shape ABCD is.
State/calculate the number of sides of the polygon.
The polygon has four sides so we are looking at a quadrilateral.
Determine the size of the angles/side lengths within the polygon.
As angles in a triangle total 180^{\circ} , angle AOD = 180 - (56+34) = 90^{\circ} . The diagonals meet perpendicularly to one another.
Recognise the other properties of the polygon.
There are two pairs of parallel sides.
The quadrilateral ABCD is a rhombus.
Example 3: quadrilateral
The polygon below is a quadrilateral. By using angle properties, determine the type of quadrilateral.
State/calculate the number of sides of the polygon.
It is stated in the question that we have a quadrilateral.
Determine the size of the angles/side lengths within the polygon.
We do not have any angles to use to classify this polygon. This in turn discounts many quadrilaterals that have specific angle properties. We can however use the information provided to find the length of AD.
As the vertical height is perpendicular to the base, we can use Pythagoras theorem to calculate the length of AD.
\begin{aligned} &5^2+12^2=AD^2\\ &25+144=AD^2\\ &AD^2=169\\ &AD=13cm \end{aligned}
Recognise the other properties of the polygon.
As the length of AD is equal to BC and the quadrilateral has one pair of parallel sides, ABCD is an isosceles trapezium.
Example 4: less than 10 sides
An octagon is made up of four congruent quadrilaterals and two congruent triangles.
By calculating the value of x , find out if the octagon is regular or irregular.
State/calculate the number of sides of the polygon.
The shape is an octagon with 8 sides.
Determine the size of the angles/side lengths within the polygon.
Looking at the quadrilateral AOMH, we can calculate the size of angle x by using the fact that angles in a quadrilateral total 360^{\circ} .
\begin{aligned} &2x+135+90=360\\ &2x=135\\ &x=67.5^{\circ} \end{aligned}
Looking at the triangle, as the line MO is parallel to the line AB, angle OAB is alternate to the angle AOM and so angle OAB = x = 67.5^{\circ} . This means that triangle ABO is isosceles as the angle at A and the angle at B are both equal.
Angle AOB = 45^{\circ} as angles in a triangle total 180^{\circ} .
Angle BAH = 67.5 + 67.5 = 135^{\circ} .
Angle ABC = 67.5 + 67.5 = 135^{\circ} and Angle BCN = 135^{\circ} as shape BCNO is congruent to shape AOMH.
Recognise the other properties of the polygon.
The line MN bisects the shape into two equal halves and so the angles on the opposite side of this line are mirrored.
All of the interior angles of the octagon are equal to 135^{\circ} and so the polygon is a regular octagon.
Example 5: less than 10 sides
A polygon has n sides. Each exterior angle is equal to 60^{\circ} . All the sides are the same length. Determine the classification of the polygon.
State/calculate the number of sides of the polygon.
As each exterior angle is equal to 60^{\circ}, we can calculate the number of sides of the polygon using the formula E_n=360 \div n where n is the number of sides and E is the exterior angle.
\begin{aligned} &60=360 \div n\\ &60 \times n=360\\ &n=360 \div 60\\ &n=6 \end{aligned}
Determine the size of the angles/side lengths within the polygon.
As we know the size of the exterior angle, we can calculate the interior angle at each vertex by using the formula I_n+E_n=180^{\circ} where I is the interior angle for the number of sides n.
\begin{aligned} &I_6+60=180\\ &I_6=120^{\circ} \end{aligned}
Each interior angle is equal to 120^{\circ} .
Recognise the other properties of the polygon.
As all of the interior angles are equal, and the polygon has 6 sides, the polygon is a regular hexagon.
Example 6: icosagon
The sum of interior angles for a polygon is 3240^{\circ} . Classify the type of polygon.
State/calculate the number of sides of the polygon.
Using the formula S_n=180(n-2) where n represents the number of sides for the polygon S, we can find the value of n.
\begin{aligned} &3240=180(n-2)\\ &n-2=3240 \div 180\\ &n-2=18\\ &n=20 \end{aligned}
Determine the size of the angles/side lengths within the polygon.
We do not know the size of any angle within the polygon so we cannot determine whether the polygon is regular or irregular.
Recognise the other properties of the polygon.
As the polygon has 20 sides, the polygon can be classified as an icosagon.
Common misconceptions
- Angles in polygons
Make sure you know your angle properties. Getting these confused can cause quite a few misconceptions.
Angles in a triangle total 180^{\circ} .
Angles in a quadrilateral total 360^{\circ} .
Angles on a straight line total 180^{\circ} .
- Incorrect quadrilateral classification
There are many quadrilaterals and it is common to confuse the properties, especially for a rhombus, parallelogram, or trapezium.
As well as this, stating that the polygon is a quadrilateral is not enough information for a classification.
- Incorrect assumptions for triangles
Assuming a triangle is isosceles or equilateral can have an impact on the size of angles within the rest of the polygon, so make sure you can explain why you have chosen a specific type of triangle.
As well as this, stating that the polygon is a triangle is not enough information for a classification. You must state whether it is isosceles/ equilateral etc.
Practice polygons questions
1. Correctly classify the following polygon.
Equilateral triangle
Isosceles triangle
Scalene triangle
Right angle triangle
Using Pythagoras theorem, we can calculate the value of angle ACB because if the sum of the square of the two shorter sides is equal to the square of the hypotenuse, the triangle is a right angle triangle.
\begin{aligned} &AB^2=3^2+4^2\\ &AB^2=9+16\\ &AB^2=25\\ &AB=5cm \end{aligned}
2. Two congruent triangles are placed adjacently with their longest edges touching. Determine the quadrilateral that is produced.
Rhombus
Trapezium
Kite
Irregular
As the two triangles are congruent, line AB = AD and line BC = CD. The angle CAD = BAC = 48^{\circ} and angle ADC = 92^{\circ} .
The angle BCA = 180-(92+48) = 40^{\circ} and is the same as angle ACD. The polygon is a kite as it has a pair of opposing angles that are equal (ABC = ADC) and one line of symmetry (AC).
3. ACE is a triangle. The line BD is parallel to line AE with angle CBD = 60^{\circ} . Classify the polygon ABDE.
Isosceles triangle
Isosceles trapezium
Equilateral triangle
Parallelogram
Angle BAE = 60^{\circ} (corresponding angles are equal)
Angles CDB = DEA = 60^{\circ} (symmetrical angles)
Angle DBA = 180-60 = 120^{\circ} (angles on a straight line total 180^{\circ} )
Angle BDE = 120^{\circ} (symmetrical to angle DBA).
The quadrilateral has one pair of parallel lines and one line of symmetry. It is an isosceles trapezium.
4. Classify the following polygon.
Regular heptagon
Regular heptadecagon
Heptadecagon
Heptagon
Angle DAM = 18^{\circ} and angle ADC = 30^{\circ} (angles in a triangle total 180^{\circ} ).
As ABC is an isosceles triangle, angle BAC = angle BCA = (180-132) \div 2 = 24^{\circ} .
As the shape has a line of symmetry, the interior angles can be duplicated to the opposite side. The sum of the interior angles is therefore equal to 900^{\circ} but the interior angles are not all the same size. This polygon is a heptagon.
5. Five congruent isosceles triangles are connected to create a pentagram. What is the classification of the polygon PQRST?
Pentagon
Regular pentagon
Pentagram
Regular pentagram
As the isosceles triangles are congruent, the side lengths of PQRST are the same size.
Angle EST = (180-36) \div 2 = 72^{\circ} so angle RST = 180-72 = 108^{\circ} .
As the angles in each isosceles triangle are congruent to the other triangles, each interior angle of the pentagon PQRST is equal to 108^{\circ} . The polygon is a regular pentagon.
6. The sum of interior angles for a polygon is 1260^{\circ} . Each interior angle is congruent. Classify the type of polygon.
Regular nonagon
Nonagon
Heptagon
Regular heptagon
As
\begin{aligned} &S_n=180(n-2)\\ &1260=180(n-2)\\ &n-2=1260 \div 180\\ &n-2=7\\ &n=9 \end{aligned}
As the polygon has 9 sides, the polygon can be classified as a regular nonagon.
Polygons GCSE questions
1. (a) Two isosceles triangles are placed together to form the polygon ABCD. What is the name of the polygon ABCD?
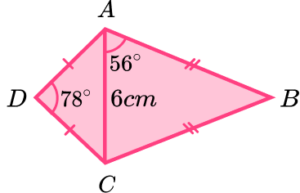
(b) Use trigonometry to calculate the length of the line AB.
(2 marks)
(a) Kite
(1)
(b)
AB=\frac{3}{\cos(56)}
(1)
AB=5.36cm \;(2dp)(1)
2. (a) What is the size of an interior angle of a regular hexagon?
(b) Six congruent triangles can tessellate to create a regular hexagon. What type of triangle are they?
(5 marks)
a) 120^{\circ}
(1)
b)
Equilateral
(1)
The interior angles of an equilateral triangle are 60^{\circ} .
(1)
The angle at the centre of the regular hexagon must be 360 \div 6=60^{\circ} .
(1)
Each internal angle is equal to 60 \times 2=120^{\circ}.
(1)
3. (a) Which of the following shapes has the greatest number of pairs of parallel sides?
Parallelogram
Trapezium
Regular hexagon
Regular octagon
(b) Two congruent polygons are joined together. Calculate the number of sides for each polygon.
(c) A regular pentagon is placed inside a regular hexagon. Calculate the size of angle x .
(7 marks)
(a) Regular octagon
(1)
(b)
36 \div 2=18
(1)
360 \div 18=20(1)
Icosagon
(1)
(c)
Interior angle in a regular hexagon = 120^{\circ} .
(1)
Interior angle in a regular pentagon = 108^{\circ} .
(1)
120-108 = 12^{\circ}(1)
Learning checklist
You have now learned how to:
- Plot specified points and draw sides to complete a given polygon
- Distinguish between regular and irregular polygons based on reasoning about equal sides and angles
- Compare and classify geometric shapes based on their properties and sizes and find unknown angles in any triangles, quadrilaterals, and regular polygons
- Describe, sketch and draw using conventional terms and notations: points, lines, parallel lines, perpendicular lines, right angles, regular polygons, and other polygons that are reflectively and rotationally symmetric
- Derive and use the sum of angles in a triangle and use it to deduce the angle sum in any polygon, and to derive properties of regular polygons
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.
Find out more about our GCSE maths tuition programme.