30 Problem Solving Maths Questions And Answers For GCSE
Problem solving maths questions can be challenging for GCSE students as there is no ‘one size fits all’ approach. Since the current GCSE specification was introduced in 2015, more exam questions involve non-routine problem solving. While following a fixed process works for simple problems, students often get stuck trying to make sense of the new information before they even begin the calculation.
Our team of expert secondary teachers created this collection of 30 problem solving maths questions and solutions to provide learners with the practice required to build confidence and skill in maths problem solving. Every question is curriculum-aligned and has been reviewed by qualified teachers who understand what works in real classrooms.
They are suitable for all students and are categorised as Foundation, Higher or crossover. As consistent practice is crucial to maths success, these problems are designed to fit into your daily lessons across the academic year, suitable for lesson starters, homework tasks or as a part of formative and summative assessment.
In addition to the problem solving maths questions, this article compiles essential advice, strategies and links to more problem solving resources to support your teaching and help your students master GCSE problem solving.
If you’re short on time, you can download the full set of 30 problem solving maths questions, solutions and strategies for free here:
30 Problem Solving Maths Questions, Solutions & Strategies
Help your students prepare for their math GCSE with these free problem solving maths questions, solutions and strategies.
Download Free Now!GCSE MATHS 2026: STAY UP TO DATE
Join our email list to stay up to date with the latest news, revision lists and resources for GCSE maths 2026. We’re analysing each paper during the course of the 2026 GCSEs in order to identify the key topic areas to focus on for your revision.
GCSE dates 2026
GCSE results (2026 when available)
Get ahead on revision with the GCSE maths papers analysis from 2025:
Analysis of GCSE Maths Paper 1 2025
Analysis of GCSE Maths Paper 2 2025
GCSE Maths Paper Analysis and Summary 2025
GCSE Maths Teacher Survey Results 2025
How to teach problem solving
In the Ofsted maths review, published in May 2021, Ofsted set out their findings from the research literature regarding the sort of curriculum and teaching that best supports all pupils to make good progress in maths throughout their time in school.
Regarding the teaching of problem solving skills and reasoning, these were their recommendations:
- Teachers could use a curricular approach that better engineers success in problem solving by teaching the useful combinations of facts and methods, how to recognise the problem types and the deep structures that these strategies pair to.
- Strategies for problem solving should be topic specific and can therefore be planned into the sequence of lessons as part of the wider curriculum. Pupils who are already confident with the foundational skills may benefit from a more generalised process involving identifying relationships and weighing up features of the problem to process the information.
- Worked examples, careful questioning and constructing visual representations can help pupils to convert information embedded in a problem into mathematical notation.
- Open-ended problem solving tasks do not necessarily mean that the activity is the ‘ideal means of acquiring proficiency’. While enjoyable, open ended problem solving questions, activities and puzzles may not necessarily lead to maths success nor improved results.
30 Problem Solving Maths Questions, Solutions & Strategies
Help your students prepare for their math GCSE with these free problem solving maths questions, solutions and strategies.
Download Free Now!7 tips to tackling problem solving maths questions
There is no ‘one size fits all’ approach to successfully tackling problem solving and reasoning questions. In KS2 and KS3, teachers may encourage students to use acronyms, such as RUCSAC (Read, Underline, Calculate, Solve, Answer, Check). While these do aim to simplify the process, it can encourage a superficial, formulaic approach to problem solving, rather than deep mathematical thinking.
However, if stuck on a maths problem, working backwards or breaking the problem down into smaller subgoals can help. Here are 7 general tips for students facing a problem solving question to avoid getting stuck, without adopting an overly formulaic approach:
- Read the whole question, underline important mathematical words, phrases or values.
- Annotate any diagrams, graphs or charts with any missing information that is easy to fill in.
- Think of what a sensible answer may look like. E.g. Will the angle be acute or obtuse? Is £30,000 likely to be the price of a coat?
- Tick off information as you use it.
- Draw extra diagrams if needed.
- Look at the final sentence of the question. Make sure you refer back to that at the end to ensure you have answered the question fully.
- Finally, check your answer – reviewing calculations for small errors and performing a sanity check helps ensure the solution is correct in context.
These tips help students to develop the necessary metacognitive skills for success in problem solving and support more independent learning.
10 problem solving maths questions (Foundation tier)
These first 10 questions and solutions are designed to be similar to Foundation GCSE Maths questions. For the first three, we’ve provided some additional strategies. The EEF suggests that showing students how to interrogate and use their existing knowledge to solve problems, such as in the example strategies listed below, is key to develop students’ problem solving skills.
In the resource download, you can find strategies for the full set of 10 Foundation questions.
1) L-shape perimeter
Here is a shape:
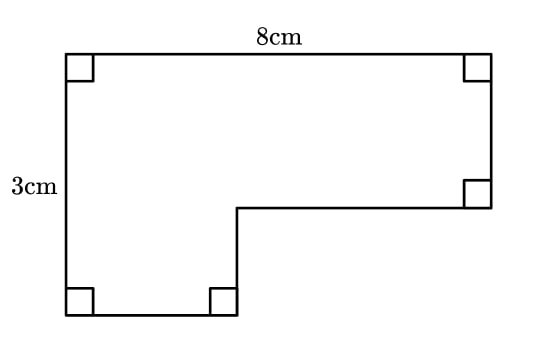
Sarah says, “There is not enough information to find the perimeter.”
Is she correct? What about finding the area?
Strategies
- Try adding more information – giving some missing sides measurements that are valid.
- Change these measurements to see if the answer changes.
- Imagine walking around the shape if the edges were paths. Could any of those paths be moved to another position but still give the same total distance?
Solution
The perimeter of the shape does not depend on the lengths of the unlabelled edges.
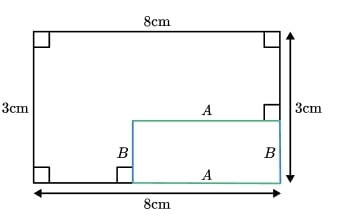
Edge A and edge B can be moved to form a rectangle, meaning the perimeter will be 22 cm. Therefore, Sarah is wrong.
The area, however, will depend on those missing side length measurements, so we would need more information to be able to calculate it.
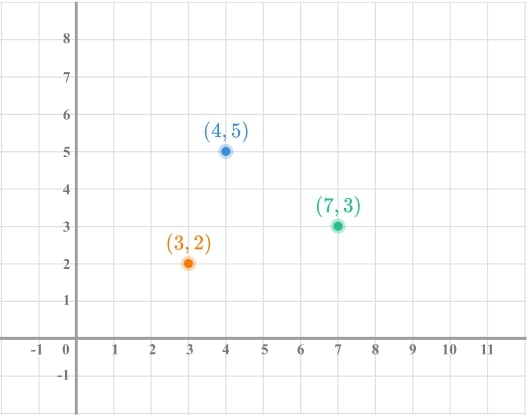
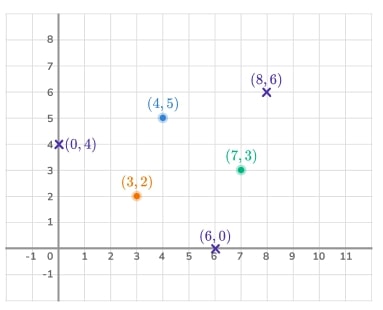
2) Find the missing point
Here is a coordinate grid with three points plotted. A fourth point is to be plotted to form a parallelogram. Find all possible coordinates of the fourth point.
Strategies
- What are the properties of a parallelogram?
- Can we count squares to see how we can get from one vertex of the parallelogram to another? Can we use this to find the fourth vertex?
Solution
There are 3 possible positions.
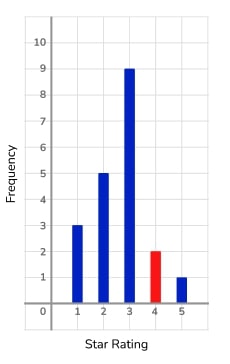
3) That rating was a bit mean!
The vertical line graph shows the ratings a product received on an online shopping website. The vertical line for 4 stars is missing.
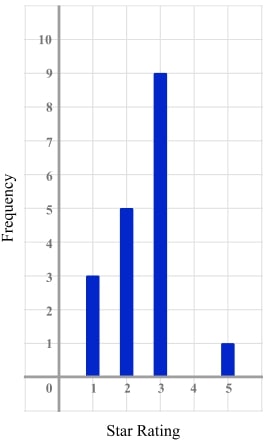
If the mean rating is 2.65, use the information to complete the vertical line graph.
Strategies
- Can the information be put into a different format, either a list or a table?
- Would it help to give the missing frequency an algebraic label, x ?
- If we had the data in a frequency table, how would we calculate the mean?
- Is there an equation we could form?
Solution
Letting the frequency of 4 star ratings be x , we can form the equation \frac{45+4x}{18+x} =2.65
Giving x=2
4) Changing angles
The diagram shows two angles around a point. The sum of the two angles around a point is 360°.
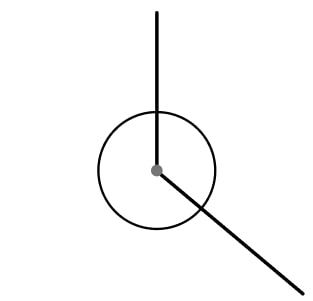
Peter says “If we increase the small angle by 10% and decrease the reflex angle by 10%, they will still add to 360°.”
Explain why Peter might be wrong.
Are there two angles where he would be correct?
Solution
Peter is wrong, for example, if the two angles are 40° and 320°, increasing 40° by 10% gives 44°, decreasing 320° by 10% gives 288°. These sum to 332°.
10% of the larger angle will be more than 10% of the smaller angle so the sum will only ever be 360° if the two original angles are the same, therefore, 180°.
5) Base and power
The integers 1, 2, 3, 4, 5, 6, 7, 8 and 9 can be used to fill in the boxes.
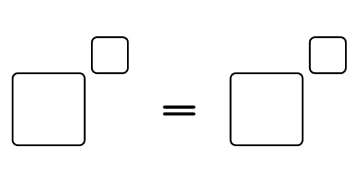
How many different solutions can be found so that no digit is used more than once?
Solution
There are 8 solutions.
23=81
26=43
29=83
32=91
34=92
38=94
43=82
49=86
6) Just an average problem
Place six single digit numbers into the boxes to satisfy the rules.

The mean in maths is 5 \frac{1}{3}
The median is 5
The mode is 3.
How many different solutions are possible?
Solution
There are 4 solutions.
2, 3, 3, 7, 8, 9
3, 3, 4, 6, 7, 9
3, 3, 3, 7, 7, 9
3, 3, 3, 7, 8, 8
7) Square and rectangle
The square has an area of 81 cm2. The rectangle has the same perimeter as the square.
Its length and width are in the ratio 2:1.
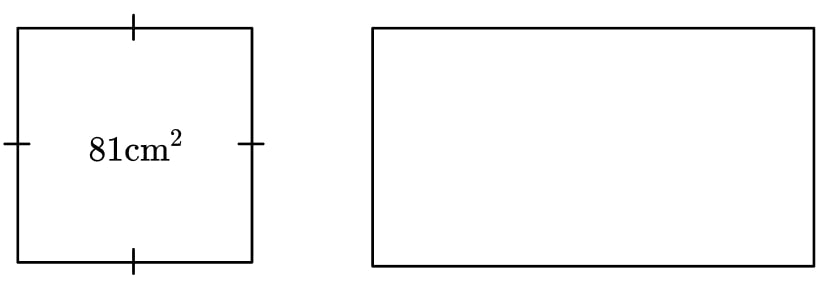
Find the area of the rectangle.
Solution
The sides of the square are 9 cm giving a perimeter of 36 cm.
We can then either form an equation using a length 2x and width x .
2x+x+2x+x=36Or, we could use the fact that the length and width add to half of the perimeter and share 18 in the ratio 2:1.
The length is 12 cm and the width is 6 cm, giving an area of 72 cm2.
8) It’s all prime
The sum of three prime numbers is equal to another prime number.
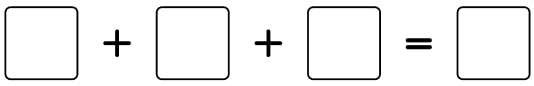
If the sum is less than 30, how many different solutions are possible?
Solution
There are 6 solutions.
- 3+5+11=19
- 3+7+13=23
- 3+7+19=29
- 5+7+11=23
- 5+7+17=29
- 5+11+13=29
2 can never be used as it would force two more odd primes into the sum to make the total even.
9) Unequal share
Bob and Jane have £10 altogether. Jane has £1.60 more than Bob. Bob spends one third of his money. How much money have Bob and Jane now got in total?
Solution
Initially Bob has £4.20 and Jane has £5.80. Bob spends £1.40, meaning the total £10 has been reduced by £1.40, leaving £8.60 after the subtraction.
10) Somewhere between
Fred says, “An easy way to find any fraction which is between two other fractions is to just add the numerators and add the denominators.” Is Fred correct?
Solution
Fred is correct. His method does work and can be shown algebraically which could be a good problem for higher tier learners to try.
If we use these two fractions \frac{3}{8} and \frac{5}{12} , Fred’s method gives us \frac{8}{20} = \frac{2}{5}
\frac{3}{8} = \frac{45}{120} , \frac{2}{5} = \frac{48}{120} , \frac{5}{12} = \frac{50}{120} . So \frac{3}{8} < \frac{2}{5} < \frac{5}{12}
10 problem solving maths questions (Foundation & Higher tier crossover)
The next 10 questions are crossover problem solving questions which could appear on both Foundation and Higher tier exam papers. We have provided solutions for each and, for the first three questions, problem solving strategies to support learners.
The strategies are provided for the full set of 10 crossover problems in the resource download.
11) What’s the difference?
An arithmetic sequence has an nth term in the form an+b.
4 is in the sequence.
16 is in the sequence.
8 is not in the sequence.
-2 is the first term of the sequence.
What are the possible values of a and b?
Strategies
- We know that the first number in the sequence is -2 and 4 is in the sequence. Can we try making a sequence to fit? Would using a number line help?
- Try looking at the difference between the numbers we know are in the sequence.
Solution
If we try forming a sequence from the information, we get this:
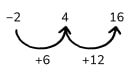
We can now try to fill in the missing numbers, making sure 8 is not in the sequence. Going up by 2 would give us 8, so that won’t work.
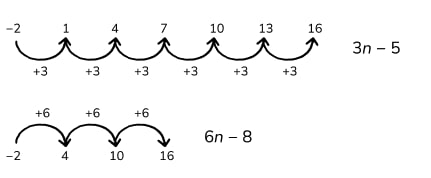
The only solutions are 6n -8 and 3n -5.
12) Equation of the hypotenuse
The diagram shows a straight line passing through the axes at point P and Q.
Q has coordinate (8, 0). M is the midpoint of PQ and MQ has a length of 5 units.
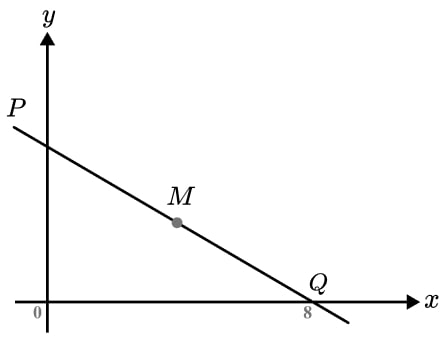
Find the equation of the line PQ.
Strategies
- We know MQ is 5 units, what is PQ and OQ?
- What type of triangle is OPQ?
- Can we find OP if we know PQ and OQ?
- A line has an equation in the form y=mx+c . How can we find m? Do we already know c?
Solution
PQ is 10 units. Using Pythagoras’ Theorem OP = 6
The gradient of the line will be \frac{-6}{8} =-\frac{3}{4} and P gives the intercept as 6.
y = - \frac{3}{4}x + 613) What a waste
Harry wants to cut a sector of radius 30 cm from a piece of paper measuring 30 cm by 20 cm.
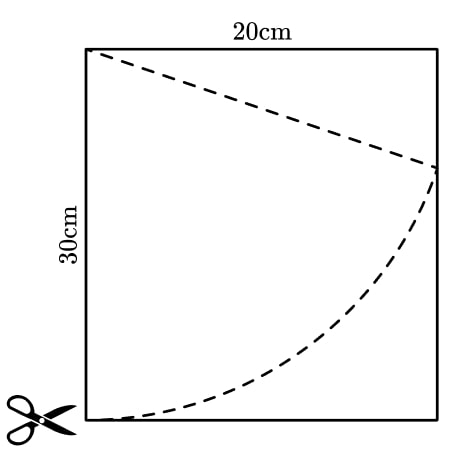
What percentage of the paper will be wasted?
Strategies
- What information do we need to calculate the area of a sector? Do we have it all?
- Would drawing another line on the diagram help find the angle of the sector?
Solution
The angle of the sector can be found using right angle triangle trigonometry.
The angle is 41.81°.
This gives us the area of the sector as 328.37 cm2.
The area of the paper is 600 cm2.
The area of paper wasted would be 600 – 328.37 = 271.62 cm2.
The wasted area is 45.27% of the paper.
14) Tri-polygonometry
The diagram shows part of a regular polygon and a right angled triangle. ABC is a straight line. Find the sum of the interior angles of the polygon.
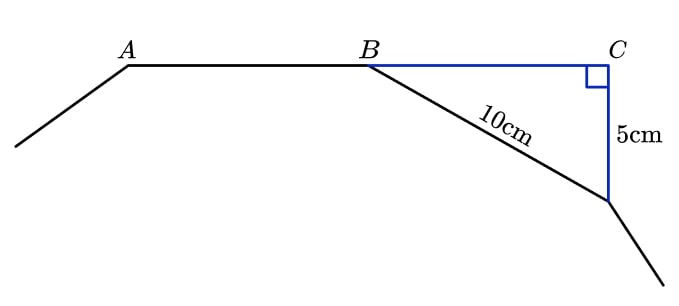
Solution
Finding the angle in the triangle at point B gives 30°. This is the exterior angle of the polygon. Dividing 360° by 30° tells us the polygon has 12 sides. Therefore, the sum of the interior angles is 1800°.
15) That’s a lot of Pi
A block of ready made pastry is a cuboid measuring 3 cm by 10 cm by 15 cm.
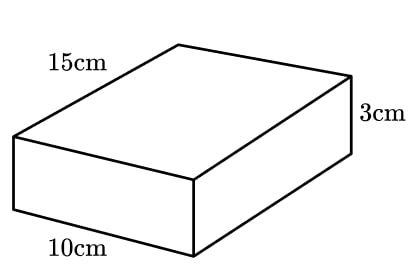
Anne is making 12 pies for a charity event. For each pie, she needs to cut a circle of pastry with a diameter of 18 cm from a sheet of pastry 0.5 cm thick.
How many blocks of pastry will Anne need to buy?
Solution
The volume of one block of pastry is 450 cm3.
The volume of one cylinder of pastry is 127.23 cm3.
12 pies will require 1526.81 cm3.
Dividing the volume needed by 450 gives 3.39(…).
Rounding this up tells us that 4 pastry blocks will be needed.
16) Is it right?
A triangle has sides of (x+4) cm, (2x+6) cm and (3x-2) cm. Its perimeter is 80 cm.
Show that the triangle is right angled and find its area.
Solution
Forming an equation gives 6x+8=80
This gives us x=12 and side lengths of 16 cm, 30 cm and 34 cm.
Using Pythagoras’ Theorem
162+302=1156
\sqrt{1156} = 34Therefore, the triangle is right angled.
The area of the triangle is (16 x 30) ÷ 2 = 240 cm2.
17) Pie chart ratio
The pie chart shows sectors for red, blue and green.
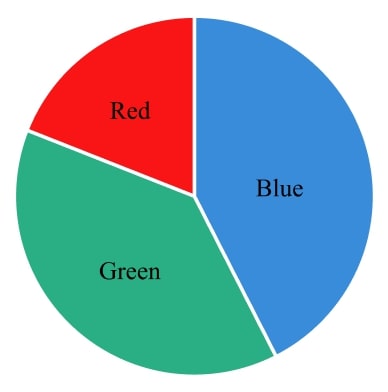
The ratio of the angles of the red sector to the blue sector is 2:7.
The ratio of the angles of the red sector to the green sector is 1:3.
Find the angles of each sector of the pie chart.
Solution
Multiplying the ratio of red:green by 2, it can be written as 2:6.
Now the colour each ratio has in common, red, has equal parts in each ratio.
The ratio of red:blue is 2:7, this means red:blue:green = 2:7:6.
Sharing 360° in this ratio gives red:blue:green = 48°:168°:144°.
18) DIY Simultaneously
Mr Jones buys 5 tins of paint and 4 rolls of decorating tape. The total cost was £167.
The next day he returns 1 unused tin of paint and 1 unused roll of tape. The refund amount is exactly the amount needed to buy a fan heater that has been reduced by 10% in a sale. The fan heater normally costs £37.50.
Find the cost of 1 tin of paint.
Solution
The sale price of the fan heater is £33.75. This gives the simultaneous equations
p+t = 33.75 and 5p+4t = 167.
We only need the price of a tin of paint so multiplying the first equation by 4 and then subtracting from the second equation gives p=32. Therefore, 1 tin of paint costs £32.
19) Triathlon pace
Jodie is competing in a Triathlon.
A triathlon consists of a 5 km swim, a 40 km cycle and a 10 km run.
Jodie wants to complete the triathlon in 5 hours.
She knows she can swim at an average speed of 2.5 km/h and cycle at an average speed of 25 km/h. There are also two transition stages, in between events, which normally take 4 minutes each.
What speed must Jodie average on the final run to finish the triathlon in 5 hours?
Solution
Dividing the distances by the average speeds for each section gives times of 2 hours for the swim and 1.6 hours for the cycle, 216 minutes in total.
Adding 8 minutes for the transition stages gives 224 minutes. To complete the triathlon in 5 hours, that would be 300 minutes.
300 – 224 = 76 minutes. Jodie needs to complete her 10 km run in 76 minutes, or \frac{19}{15} hours. This gives an average speed of 7.89 km/h.
20) Indices
a2x × ay=a3
(a3)x ÷ a4y=a32
Find x and y .
Solution
Forming the simultaneous equations
2x+y=3
Solving these gives
x=4, y=-510 problem solving maths questions (Higher tier)
This final set of 10 questions are designed to suit Higher tier students. These problem solving questions are designed to encourage critical mathematical thinking among students. Here we have just provided the solutions.
The EEF suggests that, sometimes, ‘doing’ less and talking more can have the biggest impact on students’ problem solving skills. Try asking your learners to discuss their strategies for each maths problem in the lesson before providing the answers, then have them reflect on their approaches.
21) Angles in a polygon
The diagram shows part of a regular polygon.
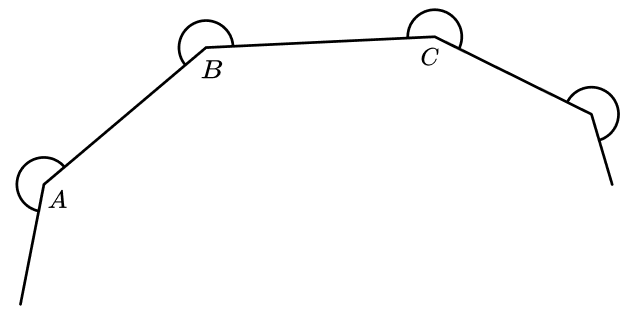
A, B and C are vertices of the polygon.
The size of the reflex angle ABC is 360° minus the interior angle.
Show that the sum of all of these reflex angles of the polygon will be 720° more than the sum of its interior angles.
Solution
Each of the reflex angles is 180 degrees more than the exterior angle: 180 + \frac{360}{n}
The sum of all of these angles is n (180 + \frac{360}{n} ).
This simplifies to 180n + 360
The sum of the interior angles is 180(n – 2) = 180n – 360
The difference is 180n + 360 – (180n -360) = 720°
22) Prism and force (Non-calculator)
The diagram shows a prism with an equilateral triangle cross-section.
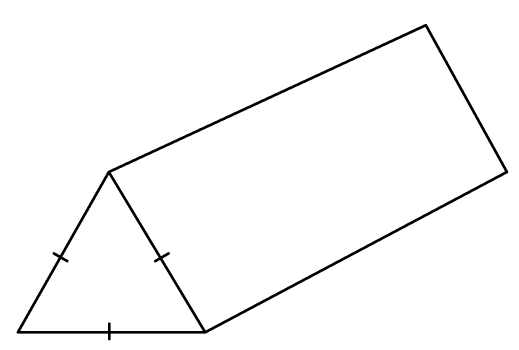
When the prism is placed so that its triangular face touches the surface, the prism applies a force of 12 Newtons resulting in a pressure of \frac{ \sqrt{3} }{4} N/m^{2}
Given that the prism has a volume of 384 m3, find the length of the prism.
Solution
Pressure = \frac{Force}{Area}
Area = 12÷ \frac{ \sqrt{3} }{4} = 16\sqrt{3} m2
Therefore, the length of the prism is 384 ÷ 16\sqrt{3} = 8\sqrt{3} m
23) Geometric sequences (Non-calculator)
A geometric sequence has a third term of 6 and a sixth term of 14 \frac{2}{9}
Find the first term of the sequence.
Solution
The third term is ar2 = 6
The sixth term is ar5 = \frac{128}{9}
Diving these terms gives r3= \frac{64}{27}
Giving r = \frac{4}{3}
Dividing the third term twice by \frac{4}{3} gives the first term a = \frac{27}{8}
24) Printing factory
A printing factory is producing exam papers. When all 10 of its printers are working, it can produce all of the exam papers in 12 days.
For the first two days of printing, 3 of the printers are broken.
At the beginning of the third day it is discovered that 2 more printers have broken down, so the factory continues to print with the reduced amount of printers for 3 days. The broken printers are repaired and now all printers are available to print the remaining exams.
How many days in total does it take the factory to produce all of the exam papers?
Solution
If we assume one printer prints 1 exam paper per day, 10 printers would print 120 exam papers in 12 days. Listing the number printed each day for the first 5 days gives:
Day 1: 7
Day 2: 7
Day 3: 5
Day 4: 5
Day 5: 5
This is a total of 29 exam papers.
91 exam papers are remaining with 10 printers now able to produce a total of 10 exam papers each day. 10 more days would be required to complete the job.
Therefore, 15 days in total are required.
25) Circles
The diagram shows a circle with equation x^{2}+{y}^{2}=13 .
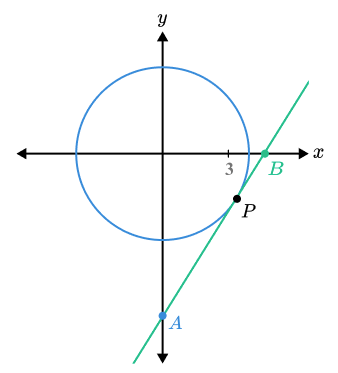
A tangent touches the circle at point P when x=3 and y is negative.
The tangent intercepts the coordinate axes at A and B.
Find the length AB.
Solution
Using the equation x^{2}+y^{2}=13 to find the y value for P gives y=-2 .
The gradient of the radius at this point is - \frac{2}{3}, giving a tangent gradient of \frac{3}{2}.
Using the point (3,-2) in y = \frac {3}{2} x+c gives the equation of the tangent as y = \frac {3}{2} x – \frac{13}{2}
Substituting x=0 and y=0 gives A and B as (0 , -\frac {13}{2}) and ( \frac{13}{3} , 0)
Using Pythagoras’ Theorem gives the length of AB as ( \frac{ 13\sqrt{13} }{6} ) = 7.812.
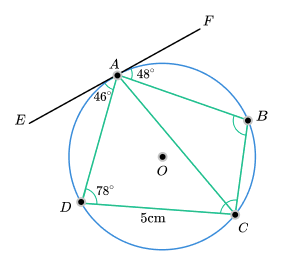
26) Circle theorems
The diagram shows a circle with centre O. Points A, B, C and D are on the circumference of the circle.
EF is a tangent to the circle at A.
Angle EAD = 46°
Angle FAB = 48°
Angle ADC = 78°
CD = 5 cm
Find the area of ABCD to the nearest integer.
Solution
The Alternate Segment Theorem gives angle ACD as 46° and angle ACB as 48°.
Opposite angles in a cyclic quadrilateral summing to 180° gives angle ABC as 102°.
Using the sine rule to find AC will give a length of 5.899.
Using the sine rule again to find BC will give a length of 3.016cm.
We can now use the area of a triangle formula to find the area of both triangles.
0.5 × 5 × 5.899 × sin(46) + 0.5 × 3.016 × 5.899 × sin(48) = 17 units2 (to the nearest integer).
27) Quadratic function
The quadratic function f(x) = -2x^{2} + 8x +11 has a turning point at P.
Find the coordinate of the turning point after the transformation -f(x-3) .
Solution
There are two methods that could be used. We could apply the transformation to the function and then complete the square, or, we could complete the square and then apply the transformation.
Here we will do the latter.
-2x^{2} + 8x + 11 -2(x^{2} - 4x) + 11 -2[(x - 2)^{2} - 4] + 11 -2 (x - 2)^{2} + 8 + 11 -2 (x - 2)^{2} + 19This gives a turning point for f(x) as (2,19).
Applying -f(x-3) gives the new turning point as (5,-19).
28) Probability with fruit
A fruit bowl contains only 5 grapes and n strawberries.
A fruit is taken, eaten and then another is selected.
The probability of taking two strawberries is \frac{7}{22} .
Find the probability of taking one of each fruit.
Solution
There are n+5 fruits altogether.
P(Strawberry then strawberry)= \frac{n}{n+5} × \frac{n-1}{n+4} = \frac{7}{22}
This gives the quadratic equation 15n^{2} - 85n - 140 = 0
This can be divided through by 5 to give 3n^{2} - 17n- 28 = 0
This factorises to (n-7)(3n + 4) = 0
n must be positive so n = 7.
The probability of taking one of each fruit is therefore, \frac{5}{12} × \frac{7}{11} + \frac {7}{12} × \frac {5}{11} = \frac {70}{132}
29) Ice cream tub volume
An ice cream tub in the shape of a prism with a trapezium cross-section has the dimensions shown. These measurements are accurate to the nearest cm.
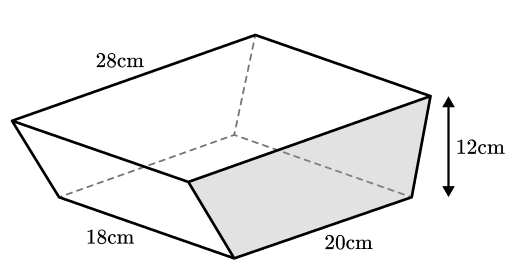
An ice cream scoop has a diameter of 4.5 cm to the nearest millimetre and will be used to scoop out spheres of ice cream from the tub.
Using bounds find a suitable approximation to the number of ice cream scoops that can be removed from a tub that is full.
Solution
We need to find the upper and lower bounds of the two volumes.
Upper bound tub volume = 5665.625 cm3
Lower bound tub volume = 4729.375 cm3
Upper bound scoop volume = 49.32 cm3
Lower bound scoop volume = 46.14 cm3
We can divide the upper bound of the ice cream tub by the lower bound of the scoop to get the maximum possible number of scoops.
Maximum number of scoops = 122.79
Then divide the lower bound of the ice cream tub by the upper bound of the scoop to get the minimum possible number of scoops.
Minimum number of scoops = 95.89
These both round to 100 to 1 significant figure, Therefore, 100 scoops is a suitable approximation the the number of scoops.
30) Translating graphs
The diagram shows the graph of y = a+tan(x-b ).
The graph goes through the points (75, 3) and Q(60, q).
Find exact values of a, b and q.
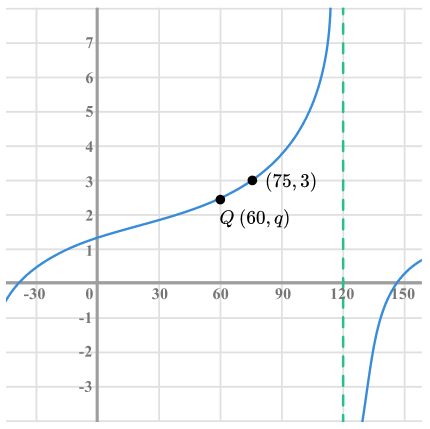
Solution
The asymptote has been translated to the right by 30°.
Therefore, b=30
75-30=45 , tan(45)=1So the point (45,1) has been translated to the point (75,3).
Therefore, a=2
y=2+tan(x-30). q=2+tan(60-30) q=2+tan(30) q=2+ \frac{\sqrt{3}}{3} = \frac{6 + \sqrt{3}}{3}Reflecting on problem solving maths questions
Whether students reach a correct answer or not, reflecting on the problem solving process can lead to insights about more efficient methods in the future. The EEF recommends a ‘debrief’ after completing problem solving and suggests the following questions to prompt students’ reflections:
- What exactly did you do?
- Why did this help you?
- What was challenging? Why?
- Is there a better way to…?
- What changes would you make? Why?
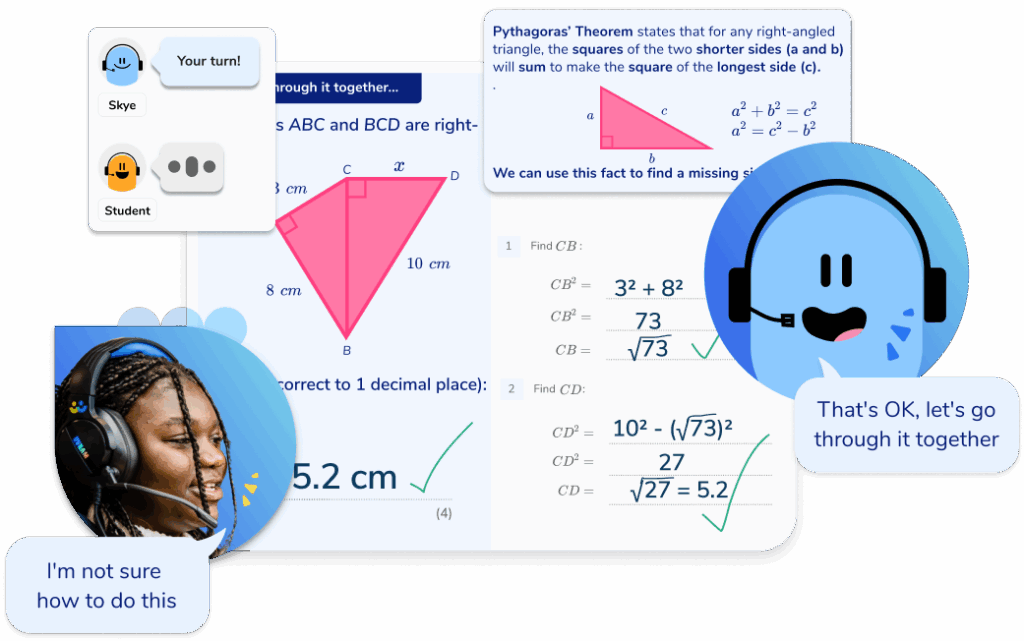
Verbalisation, questioning and discussion are key principles that underpin the approach that Third Space Learning’s AI GCSE maths tutoring with Skye takes when tackling problem solving questions.
When a learner encounters a difficulty or makes an error, Skye provides up to three carefully scaffolded hints to encourage perseverance and guide the pupil toward the correct answer independently.
Skye is trained to develop students’ metacognitive skills by using open-ended questions to prompt students to verbalise their reasoning and reflect on their thought processes. This moves students beyond simply learning how to solve a single, unique problem and towards a more comprehensive understanding of problem solving.
Staff all commented on how the students were having to explain their thinking. You can hear that the tutor really dive into ‘why did you do that?’ and ‘can you explain your answer?’. It was really nice to hear the mathematical language in the room.
Nick Clark, Director of Learning for Maths, George Eliot Academy
We hope these problem solving maths questions will support your GCSE teaching and discussion in class. To get the full set of questions, solutions and strategies in a printable form, please download the resource.
Make sure you also check out other websites such as NRICH and STEM Learning for more curriculum-aligned problem solving resources, maths problems, and puzzles for your GCSE class. The UKMT also offers a mentoring scheme that provides problem solving resources complete with answers.
Looking for additional support, maths problems and problem solving resources for KS3 & KS2?
These tips suggested in this blog are not exclusive to KS4 students, and most are suitable for KS2 problem solving and KS3 maths problem solving.
Many of the secondary maths resources published in Third Space Learning’s resource library will be suitable for KS3 learners and are available to download for free. There is a section devoted to GCSE maths revision with plenty of maths worksheets and GCSE maths questions. There are also free maths tests for KS3 students:
If you’re a KS2 teacher needing more support teaching reasoning, problem solving & planning for depth, we have a whole set of word problems and teaching strategies designed to engage and support your class.
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Skye – our AI maths tutor built by teachers – gives students personalised one-to-one lessons that address learning gaps and build confidence.
Since 2013 we’ve taught over 2 million hours of maths lessons to more than 170,000 students to help them become fluent, able mathematicians.
Explore our AI maths tutoring or find out about an online maths tutor for your school.