BODMAS Questions That Will Test Your Primary School Pupils

BODMAS, also known as BIDMAS, is an acronym to help remember the order of operations, the correct order in which mathematical operations must be completed. It stands for Brackets, Power Of, Division, Multiplication, Addition and Subtraction. Pupils are first introduced to BODMAS in Year 6, with predominantly arithmetic questions containing two or three different operations. It is a key concept for learners to understand and lays an important foundation for maths beyond KS2. 

As maths tutoring providers, we work with thousands of Year 6 pupils every year as they begin to tackle BODMAS questions. In this article, we share what we’ve learned, some of the common misconceptions and a range of worked examples, as well as links to more resources, including a BODMAS questions worksheet, to support your classroom teaching.

What are BODMAS questions?

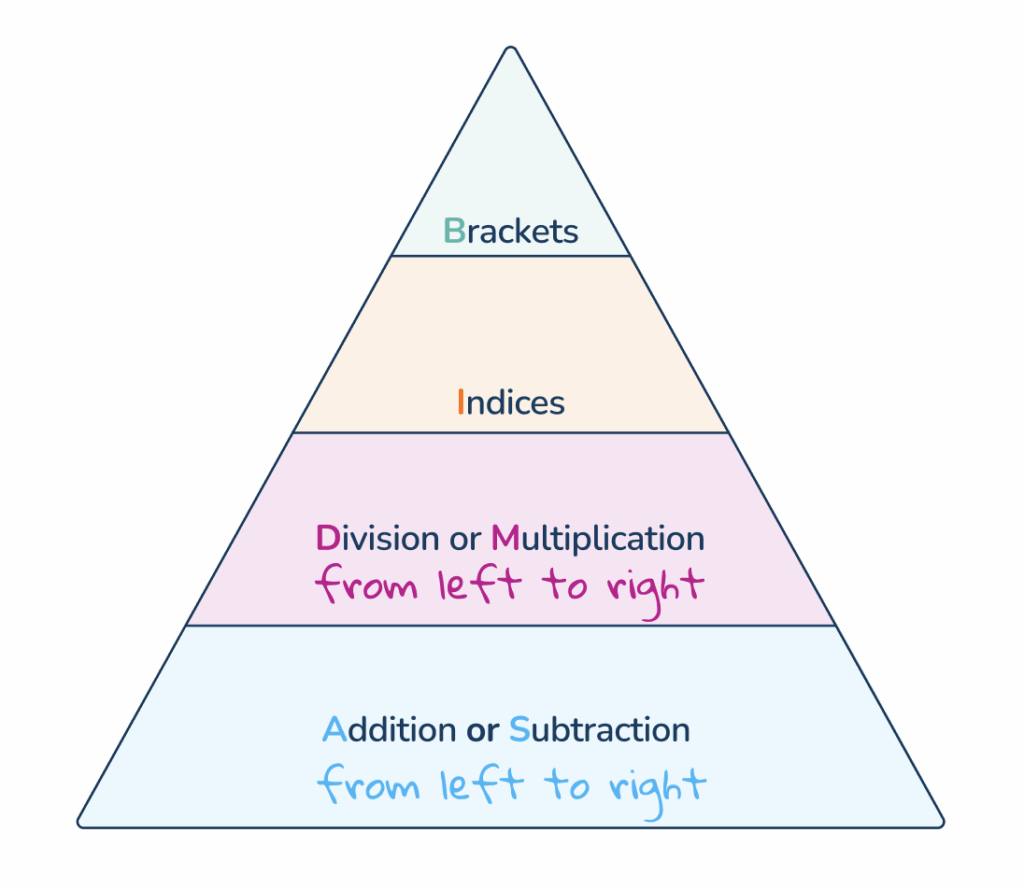
BODMAS represents the correct order of operations. The letters of BODMAS are a mnemonic that helps learners remember the order of operations in mathematics. This agreed-upon rule is essential for establishing mathematical consistency, ensuring that everyone evaluates an expression in the same way to reach the single correct answer.

BODMAS rule

BODMAS stands for:

1. B rackets
2. Powers O f
3. D ivision and M ultiplication
4. A ddition and S ubtraction

This means that when calculating a mathematical expression, you must follow this specific hierarchy rather than simply working from left to right. You begin by solving any parts in brackets, followed by indices. Next, you divide and multiply (working from left to right), and finally, you perform addition and subtraction.

BODMAS is also referred to as BIDMAS, in which case the letters stand for:

1. B rackets
2. I ndices (e.g. powers, square numbers and square roots)
3. D ivision and M ultiplication
4. A ddition and S ubtraction

A common misconception regarding BODMAS is that division takes precedence over multiplication, or addition over subtraction; however, multiplication and division have equal priority, as do addition and subtraction (but less so than multiplication and division). In the BODMAS rule, these operations are completed from left to right (although addition and subtraction can actually be completed in any order and still achieve the same answer).

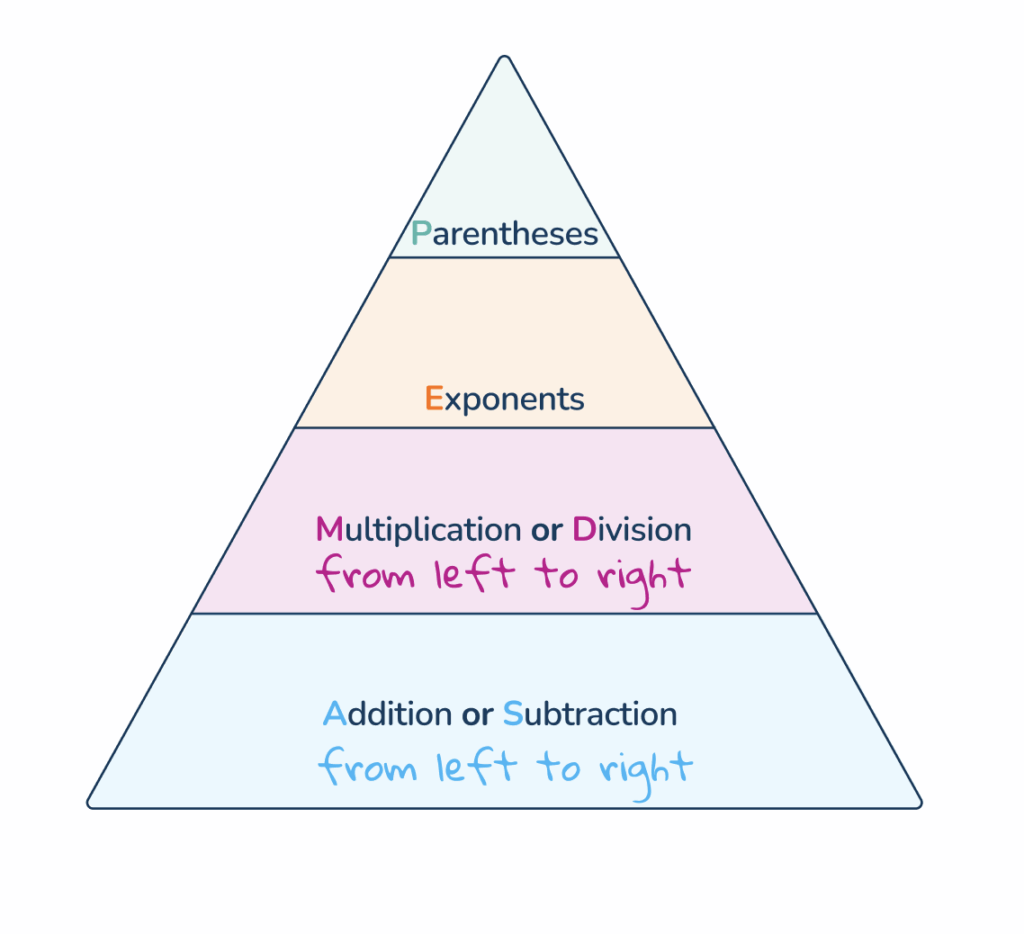
PEMDAS is the American equivalent to help learners complete calculations in the correct order. In this version, the letters of the acronym stand for:

1. P arentheses
2. E xponents
3. M ultiplication and D ivision
4. A ddition, and S ubtraction.

As with BODMAS and BIDMAS, multiplication and division have equal priority, as do addition and subtraction and these operations are completed from left to right.

How to solve BODMAS questions

BODMAS question worked example 1 

Question: 50 – 4² x 3

BODMAS method: 

4² = 16

50 – 16 x 3 = 

16 x 3 = 48

50 – 48 = 2 

Explanation: The correct answer is 2; without using the correct order of operations, this question would be incorrectly calculated as 102 (50 – 16 is 34, 34 x 3 = 102). See below for a step by step explanation using BODMAS:

1. Brackets
   There are no brackets in this question.
2. Powers Of (or Indices in BIDMAS)
   42 is 16. The question now becomes 50 – 16 x 3.
3. Division and Multiplication
   Calculate 16 x 3 which equals 48.
4. Addition and Subtraction
   Calculate 50 – 48 which equals 2.

BODMAS question worked example 2 

Question: 36 + (28 ÷ 7) – 18

BODMAS method:

28 ÷ 7 = 4

36 + 4 = 40

40 – 18 = 22

Explanation: The correct answer is 22. Pupils may find this question confusing as they will need to do both addition and subtraction. Neither of these take priority and pupils will reach the same answer whether they complete either operation first. See below for a step by step explanation:

1. Brackets
   Solve inside brackets first: 28 ÷ 7 = 4
2. Powers Of (or Indices in BIDMAS)
   There are no indices in this question.
3. Division and Multiplication
   There is no division or multiplication outside the brackets in this question.
4. Addition and Subtraction
   The question now reads 36 + 4 – 18. Addition and subtraction can be done in any order: if we did the addition first (36 + 4 = 40) and solved the calculation from left to right, then 40 – 18 = 22. If we did the subtraction first (4 = 18 = -14) and then the addition, then 36 + -14 = 22.

BODMAS question worked example 3

Question: 40 ÷ 2³ + (5-2)

BODMAS method:

5 – 2 = 3

2³ = 8

40 ÷ 8 = 5

5 + 3 = 8

Explanation: The correct answer is 8. Pupils might incorrectly solve from left to right (40 ÷ 2 = 20, 20³ = 8000, etc.), resulting in a vastly different and incorrect answer. See below for a step by step explanation using BODMAS:

1. Brackets
   Solve inside the brackets first: 5 – 2 = 3. The question now becomes: 40 ÷ 2³ + 3.
2. Powers Of (or Indices in BIDMAS)
   Calculate the index. 2³ means 2 x 2 x 2, which equals 8. The question now becomes: 40 ÷ 8 + 3.
3. Division and Multiplication
   Perform the division before the addition. Calculate 40 ÷ 8 which equals 5. The question  now reads: 5 + 3.
4. Addition and Subtraction
   Calculate 5 + 3 = 8.

BODMAS in the KS2 National Curriculum

Primary pupils start learning about order of operations in Year 6 maths lessons. The National Curriculum states that in the number (addition, subtraction, multiplication and division) unit, Year 6 pupils “should be taught to use their knowledge of the order of operations to carry out calculations involving the four operations”. In the non-statutory guidance, the NC suggests that “pupils explore the order of operations using brackets; for example, 2 + 1 x 3 = 5 and (2 + 1) x 3 = 9.”

This builds on previous learning from Year 5 number (multiplication and division): to recognise and use square numbers and cube numbers, and the notation for squared (²) and cubed (³).

BODMAS questions Year 6

• 2³ + 5 x 4

1. Power of (2³ = 2 cubed = 2 x 2 x 2 = 8)
2. Multiply (5 x 4 = 20)
3. Addition (8 + 20 = 28)

• 60 – 21 ÷ 3

1. Division (21 ÷ 3 = 7)
2. Subtract (60 – 7 = 53)

Completing the operations in the correct order (division then subtraction) would result in the correct answer of 53. However, this is a good question to assess the children’s knowledge of BODMAS because the answer could also seem ‘easy’ if performed incorrectly, as 60 – 21 = 39, which is easily divided by 3 (13).

• 36 ÷ (11 – 7)

1. Brackets first. Perform the subtraction inside (11 – 7 = 4)
2. Complete the division (36 ÷ 4 = 9).

BODMAS SATs questions

Since the introduction of the new curriculum in 2016, BODMAS questions have appeared a number of times throughout the SATs papers: notably, it is only in 2019 that questions requiring BODMAS began to show up in both the reasoning and arithmetic papers; prior to this, they were only in the arithmetic tests. 

Now, pupils need to develop not only fluency in using BODMAS, but also the ability to apply the BODMAS principle to more complex, problem-solving, or contextual scenarios.

SATs arithmetic questions and answers (each worth 1 mark)

SATs year	Question	Answer	Answer without BODMAS (common misconception)
2016	60 – 42 ÷ 6	53	3
2016	32 + 10 =	19	Not a BODMAS misconception, but some children misunderstand 32 to mean 3×2 as opposed to 3×3
2017	50 + (36 ÷ 6) =	56	86/6 or 14r2
2018	92 – 36 ÷ 9 =	77	5
2018	62 + 10 =	46	Not a BODMAS misconception, but some children misunderstand 62 to mean 6×2 as opposed to 6×6
2019	60 ÷ (30 − 24) =	10	-22
2022	6 + 4 ÷ 2 =	8	5
2023	70 + 48 ÷ 6 =	78	19.67
2024	90 − 56 ÷  8 =	83	4.25
2025	(52 + 3) − 12 ÷ 4 =	52	10.75

SATs reasoning questions and answers using BODMAS

SATs year	Question	Answer	Answer without BODMAS (common misconception)
2019	A theme park sells tickets online. Each ticket costs £24. There is a £3 charge for buying tickets. Which of these shows how to calculate the total cost, in pounds? Choose one. a) number of tickets x 3 + 24 b) number of tickets x 24 + 3 c) number of tickets + 3 x 24 d) number of tickets + 24 x 3	b)	Any of the others. Teachers should encourage students to always consider the order of operations when calculating multi-step expressions.
2019	Write the missing number. 6 + 2 x 2 – ? = 6	4	10
2024	Sarah makes jewellery using black and white beads. She uses this rule to work out how many black beads to use. black = (white × 3) + 4Sarah uses 25 black beads to make a bracelet. How many white beads does she use?	7	Pupils following from left to right could still achieve the correct answer, but may attempt to perform the calculations with the known numbers first. (3 + 4 =7, 25 ÷ 7 = 3.57)
2025	Jack buys four concert tickets. Each ticket costs £28. Tick each calculation that Jack could use to work out the total cost. One has been done for you. 28 + 28 + 28 + 28 ✓  a) (20 × 4) + (8 × 4) b) (4 × 20) + 8 c) (4 × 30) – (4 × 2)  d) (4 × 30) – 2	a) &  c)	(4 × 20) + 8 = 88 & d) (4 × 30) – 2 = 118

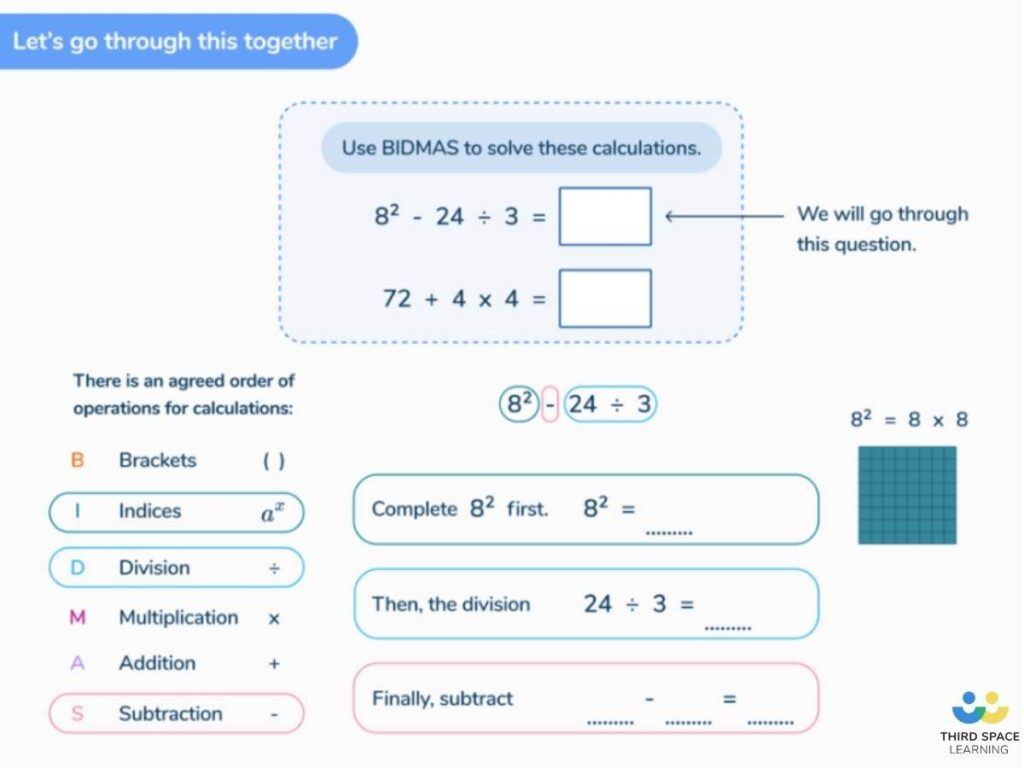
Simple BODMAS questions

BODMAS questions can be simplified by limiting the number of operations used or making the calculations themselves simple. Another way to simplify BODMAS questions (although this doesn’t directly assess children’s knowledge of the order of operations) is by ensuring that there is only one possible answer even without the use of BODMAS.

• (4 x 3) + 12

1. Brackets first (4 x 3 = 12)
2. Addition (12 + 12 = 24)

We would calculate the multiplication first here, whether the brackets are present or not. Mathematically, the presence of the brackets is unnecessary, but it is useful to expose children to this notation.

• 20 – 9 ÷ 3

1. Division (9 ÷ 3 = 3)
2. Subtract 3 from 20 (20 – 3 = 17)

Hopefully children will realise that without BODMAS, this becomes overly complicated to calculate (11 ÷ 3 is tricky to perform).

• 2² + 5

1. Indices (2² = 4)
2. Addition (4 + 5 = 9)

This question involving indices is forgiving of common mistakes. Even if a student incorrectly interprets the squared notation as doubling, the value remains 4. With such a simple layout, the order of operations is clear.

Difficult BODMAS questions

• Put brackets into this expression to make it correct: 10² ÷ 10 ÷ 10 ÷ 10 ÷ 10 = 100

There are many different answers to this question, including brackets within brackets:
10² ÷ (10 ÷ 10) ÷ (10 ÷ 10) = 100
10²  ÷ ((10 ÷ 10) ÷ 10)) ÷ 10 = 100
(10² ÷ 10) ÷ ((10 ÷ 10) ÷ 10) = 100
10² ÷ (10 ÷ (10 ÷ (10 ÷ 10))) = 100
10² ÷ (10 ÷ (10 ÷ 10) ÷ 10) = 100
10² ÷ (10 ÷ 10 ÷ (10 ÷ 10)) = 100

• Here are five numbers: \frac{1}{2}     1 \frac{1}{2}     2     2 \frac{1}{2}     3 \frac{1}{2}
  Use three of the numbers to make this calculation correct: (? + ?) x ? = 10

Whilst the BODMAS element of this isn’t too difficult, it is made more complex with the inclusion of fractions. There are two possible answers to this question:
(1 \frac{1}{2} + 3 \frac{1}{2} ) x 2
( \frac{1}{2} + 3 \frac{1}{2} ) x 2 \frac{1}{2}   

• Write the correct missing operation to make the calculation correct: 18 __ 3 x 5 = 30

18 ÷ 3 x 5 = 30

• Write the missing number: 48 ÷ (19 – ?) = 4

1. Brackets must be solved first. 
2. Looking at 48 ÷ ? = 4, we can see the missing amount must be 12 so the calculation in the brackets must also equal 12.
3. 19 – 7 = 12
4. The answer is therefore 48 ÷ (19 – 7) = 4.

• Write the missing number: ? + 6 x 8 = 56

1. Multiplication must be solved first.
2. 6 x 8 = 48. 3. The question then becomes ? + 48 = 56.
3. 56 – 48 = 8 so the answer is 8 + 6 x 8 = 56.

• 20 ÷ \frac{1}{2} x 3 – 4

1. Divide 20 by the fraction \frac{1}{2} (which is the same as multiplying by 2) (20 ÷ \frac{1}{2} = 40)
2. Multiply that result by 3 (40 x 3 = 120)
3. Finally, subtract 4 (120 – 4 = 116)

This calculation contains a common trap. Because multiplication and division are of equal priority, you must work from left to right.

BODMAS beyond primary 

Whilst there isn’t a direct mention of the ‘order of operations’ in the secondary maths curriculum, the KS3 maths and GCSE maths curriculums do require pupils to “use conventional notation for the priority of operations, including brackets, powers, roots and reciprocals” and to “recognise and use relationships between operations, including inverse operations”. Therefore, the importance of the BODMAS rule extends far beyond primary school. This key concept must be introduced and taught effectively in KS2 maths to prevent common misconceptions and ensure students possess the fluency needed for GCSE success.

We hope this guide has provided clear strategies to address common misconceptions and build confidence within your class using BODMAS and BIDMAS. Remember to download our Year 6 BODMAS worksheet to provide your pupils with more practice. To further support your classroom teaching and ensure every pupil is ready for their SATs, explore our additional national curriculum aligned resources below.