High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Mean, median and mode Grouped frequency table Addition and subtraction Multiplication and division

Math resources Statistics and probability Freq. table

Mean from a freq. table

Mean from a frequency table

Here you will learn about the mean from a frequency table, including what it is and how to calculate it. You will also learn how to find an estimate for the mean from a grouped frequency table.

Students will first learn about mean from a frequency table as part of statistics and probability in $6$ th grade.

What is mean from a frequency table?

Mean from a frequency table is when you find the mean average from a data set which has been organized into a frequency table. The frequency is the number of times a number or item is recorded in a data set.

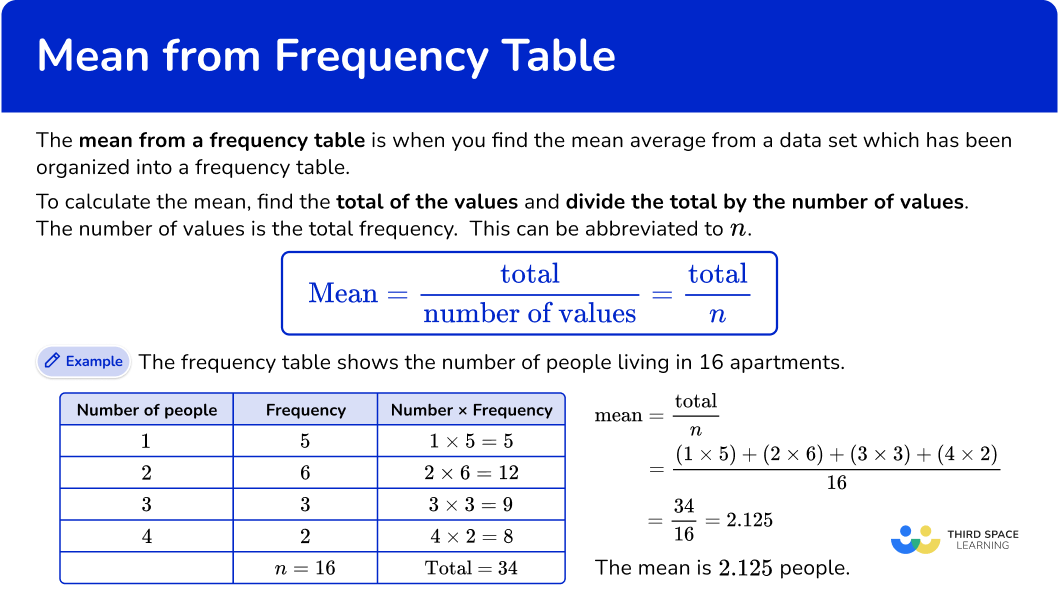
To calculate the mean, find the total of the values and divide the total by the number of values. The number of values is the total frequency. This can be abbreviated to $n.$

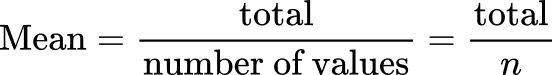
You can use an extra column to help.

Mean is a measure of central tendency. It is a value that can be used to represent a set of data.

For example,

The frequency table shows the number of people living in $16$ apartments.

There are $5$ apartments with $1$ person living there, so calculate $1 \times 5=5$

There are $6$ apartments with $2$ people living there, so calculate $2 \times 6=12$

There are $3$ apartments with $3$ people living there, so calculate $3 \times 3=9$

There are $2$ apartments with $4$ people living there, so calculate $2 \times 4=8$

The number of values $(n)$ is the total frequency, here $n=16.$

$\text{Mean}=\cfrac{\text{total}}{n}=\cfrac{(1\times 5)+(2\times 6)+(3\times 3)+(4\times 2)}{16}=\cfrac{34}{16}=2.125$

The mean is $2.125$ people.

[FREE] Mean from a Frequency Table Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of mean from a frequency table. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Mean from a Frequency Table Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of mean from a frequency table. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

Estimated mean from a grouped frequency table

When the data has been grouped together and put into a grouped frequency table, you cannot find the actual mean because you only have a range of possible values.

Instead you can find an estimate for the mean using the midpoints of each group. You can add more columns to the grouped frequency table to help.

For example,

The frequency table shows the number of correct answers earned on a test by $20$ students.

There were $3$ people who answered between $0 \text{-}9$ questions correctly. As you don’t know the exact number of questions that each of these people got correct, you will use the midpoint of $4.5$ questions correct.

You can find the midpoint by adding the smallest value and the largest value together and dividing by $2.$

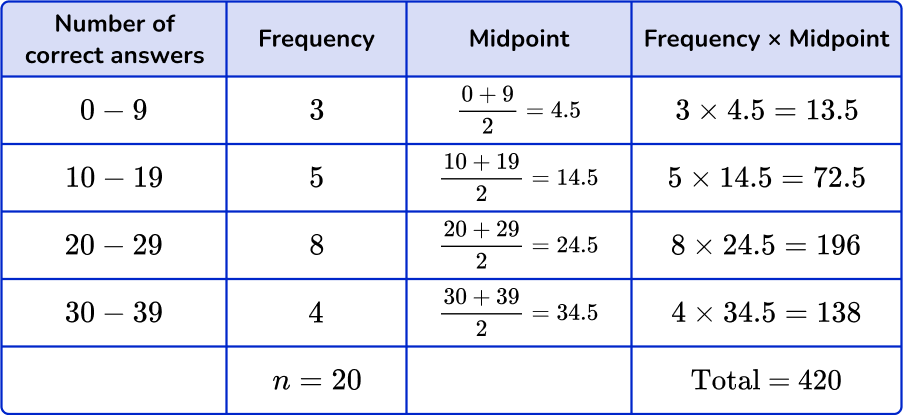
$\text{Estimated Mean}=\cfrac{\text{total}}{n}=\cfrac{420}{20}=21$

The estimated mean is $21$ questions correct.

What is mean from a frequency table?

Common Core State Standards

How does this relate to $6$ th grade math?

Grade 6: Statistics and Probability (6.SP.A.3)
Recognize that a measure of center for a numerical data set summarizes all of its values with a single number, while a measure of variation describes how its values vary with a single number.

How to find the mean from a frequency table

In order to calculate the mean from a frequency table, you need to:

Multiply the number values by the frequencies.
Find the totals.
Divide the total by $\textbf{n}.$

Mean from a frequency table examples

Example 1: frequency table

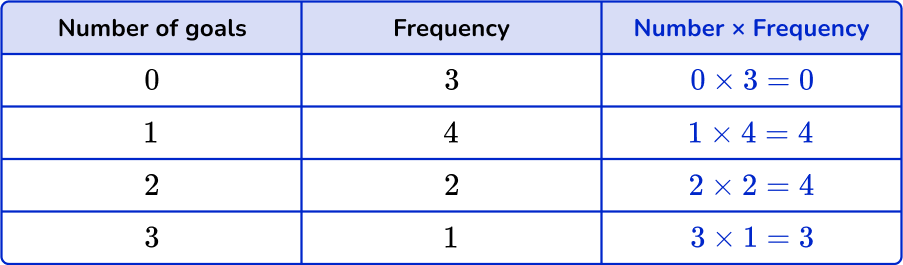
The frequency table shows the number of goals scored in $10$ soccer games. Find the mean number of goals.

Multiply the number values by the frequencies.

You can add an extra column next to the frequency column to help find the subtotals.

2Find the totals.

Find the total of the frequency column, $n.$ Add up the subtotals to find the total.

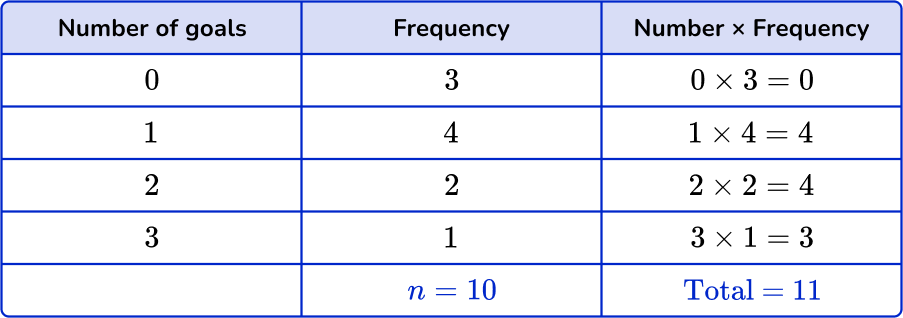
3Divide the total by $\textbf{n}.$

The last step is to divide the total by $n.$

$\text{Mean}=\cfrac{\text{total}}{n}=\cfrac{11}{10}=1.1$

The mean is $1.1$ goals.

Example 2: frequency table

The frequency table shows the number of people on $20$ buses. Find the mean number of people.

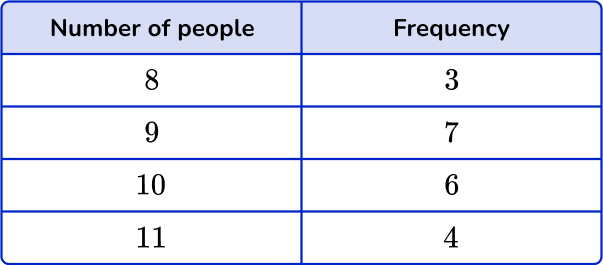
Multiply the number values by the frequencies.

You can add an extra column next to the frequency column to help find the subtotals.

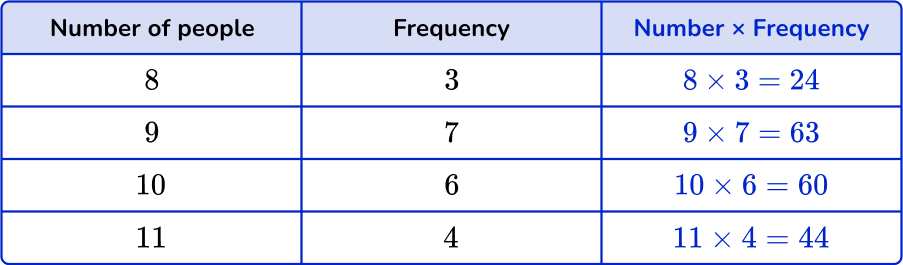
Find the totals.

Find the total of the frequency column, $n.$ Add up the subtotals to find the total.

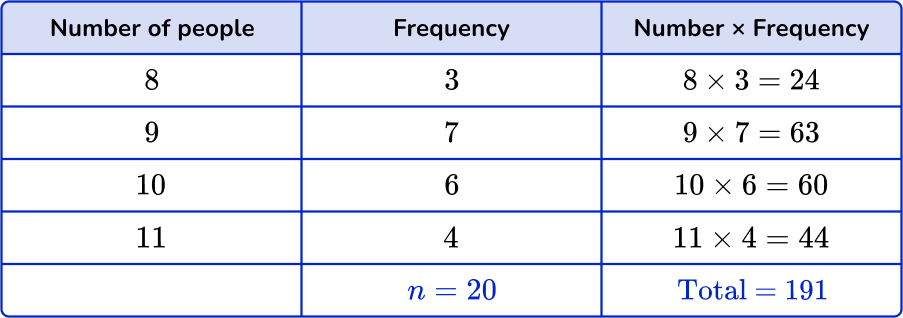
Divide the total by $\textbf{n}.$

The last step is to divide the total by $n.$

$\text{mean}=\cfrac{\text{total}}{n}=\cfrac{191}{20}=9.55$

The mean is $9.55$ people.

Example 3: frequency table

The frequency table shows the ages, in years, of $25$ children in a math club. Find the mean age.

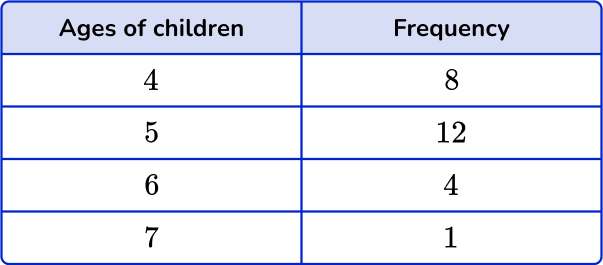
Multiply the number values by the frequencies.

You can add an extra column next to the frequency column to help find the subtotals.

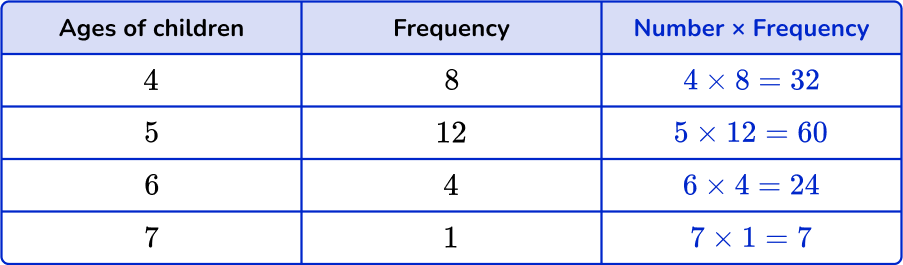
Find the totals.

Find the total of the frequency column, $n.$ Add up the subtotals to find the total.

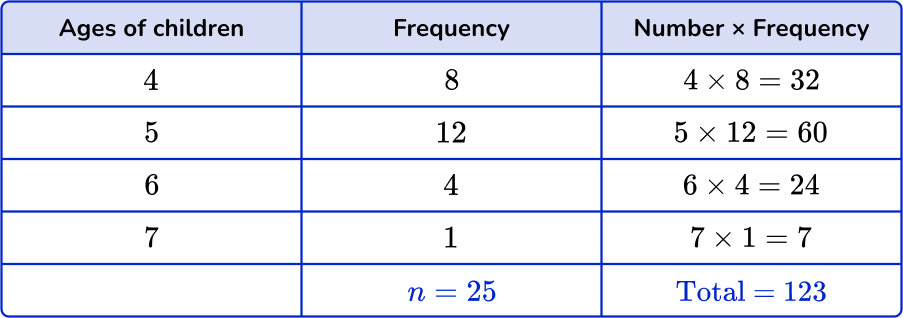
Divide the total by $\textbf{n}.$

The last step is to divide the total by $n.$

$\text{Mean}=\cfrac{\text{total}}{n}=\cfrac{123}{25}=4.92$

The mean is $4.92$ years.

How to estimate the mean from a grouped frequency table

In order to estimate the mean from a grouped frequency table, you need to:

Find the midpoints of the groups.
Multiply midpoints by the frequencies.
Find the totals.
Divide the total by $\textbf{n}.$

Example 4: grouped frequency tables

The grouped frequency table shows the number of people in $10$ train carriages.

Estimate the mean number of people.

Find the midpoints of the groups.

You do not know the actual number of people in the groups, so use the midpoint.

Find the midpoint by adding the smallest value and the largest value together and dividing by $2.$ Add a column for the midpoints.

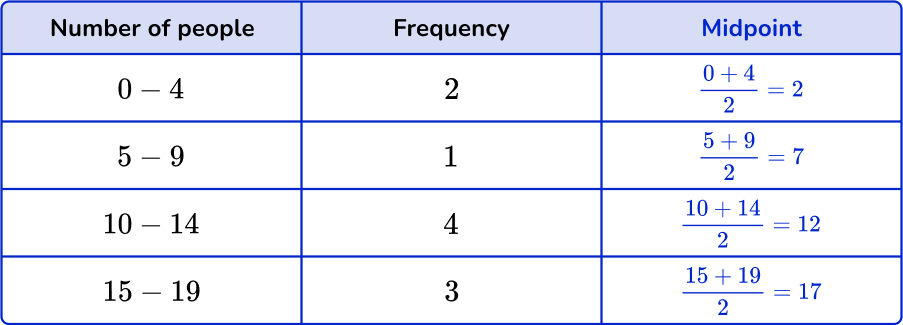
Multiply midpoints by the frequencies.

You can add an extra column next to the frequency column to help find the subtotals.

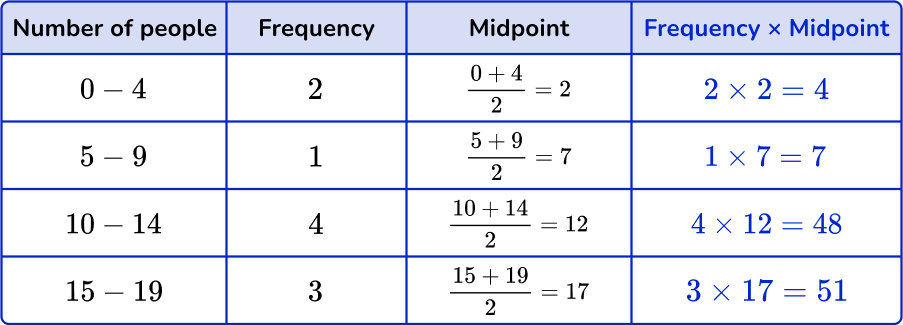
Find the totals.

Find the total of the frequency column, $n.$ Add up the subtotals to find the total.

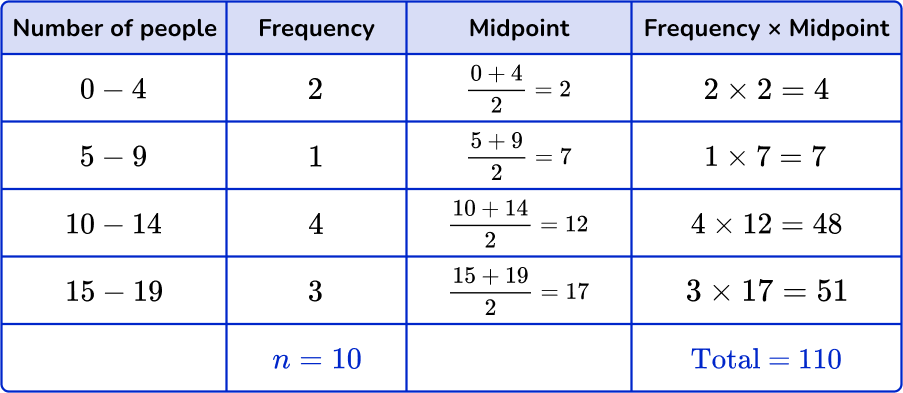
Divide the total by $\textbf{n}.$

The last step is to divide the total by $n.$

$\text{mean}=\cfrac{\text{total}}{n}=\cfrac{110}{10}=11$

But remember that this is an estimate for the mean.

The estimated mean is $11$ people.

Example 5: grouped frequency tables

The grouped frequency table shows the ages of $25$ people in a department store.

Estimate the mean age.

Find the midpoints of the groups.

You do not know the actual ages in the groups, so use the midpoint.

Find the midpoint by adding the smallest value and the largest value together and dividing by $2.$ Add a column for the midpoints.

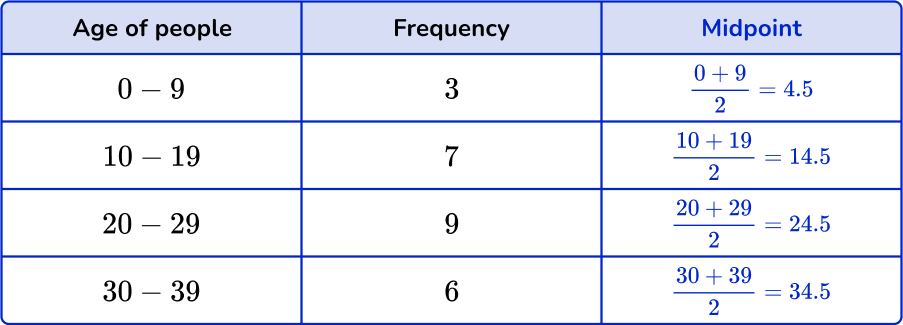
Multiply midpoints by the frequencies.

You can add an extra column next to the frequency column to help find the subtotals.

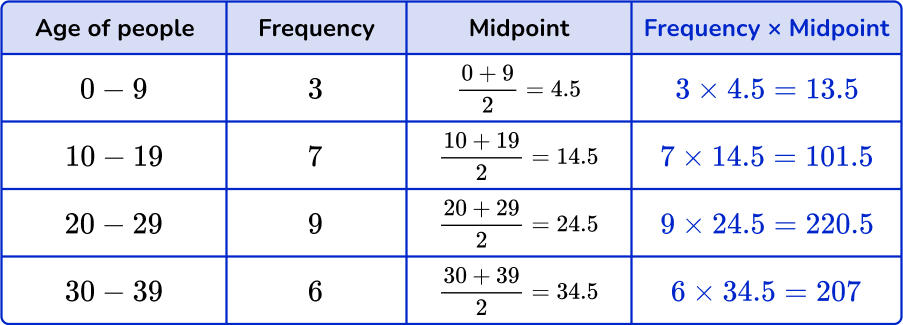
Find the totals.

Find the total of the frequency column, $n.$ Add up the subtotals to find the total.

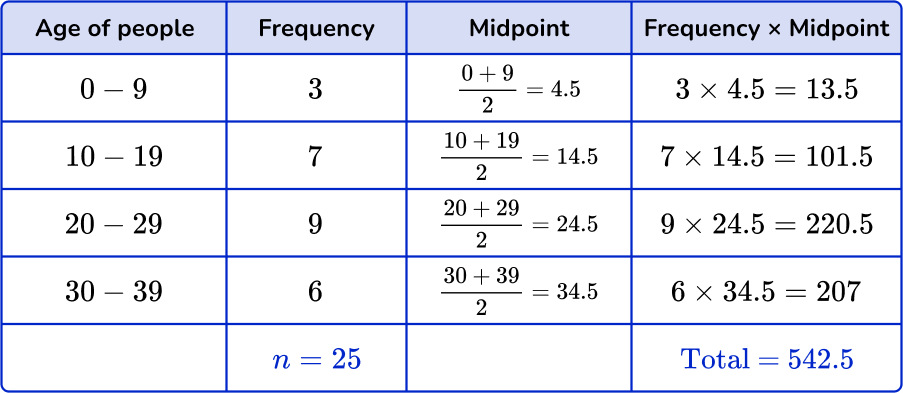
Divide the total by $\textbf{n}.$

The last step is to divide the total by $n.$

$\text{Mean}=\cfrac{\text{total}}{n}=\cfrac{542.5}{25}=21.7$

But remember that this is an estimate for the mean.

The estimated mean is $21.7$ marks.

Example 6: grouped frequency tables

The grouped frequency table shows the weight in grams of $30$ potatoes.

Estimate the mean weight. Round your answer to the nearest tenths.

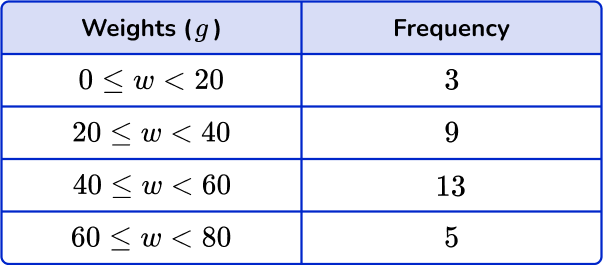
Find the midpoints of the groups.

You do not know the actual weights in the groups, so use the midpoint.

Find the midpoint by adding the smallest value and the largest value together and dividing by $2.$ Add a column for the midpoints.

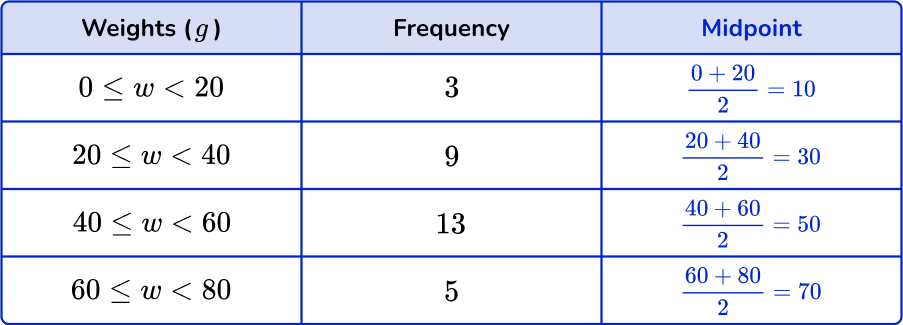
Multiply midpoints by the frequencies.

You can add an extra column next to the frequency column to help find the subtotals.

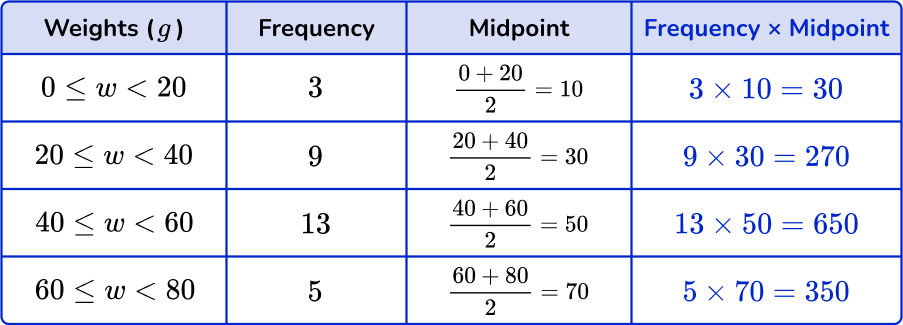
Find the totals.

Find the total of the frequency column, $n.$ Add up the subtotals to find the total.

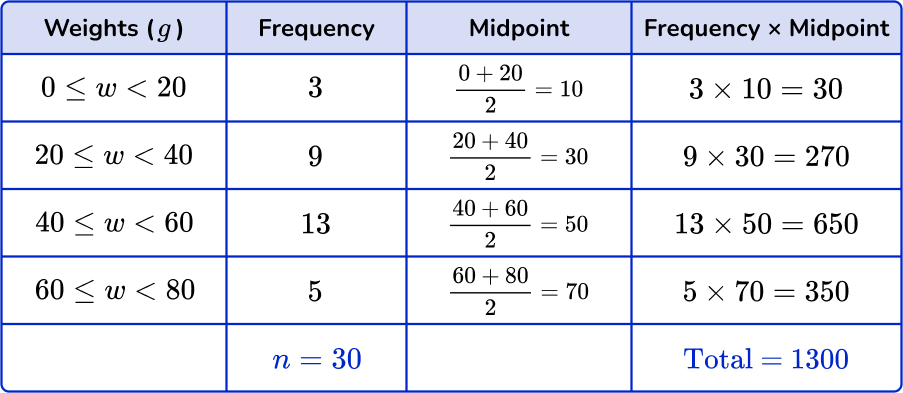
Divide the total by $\textbf{n}.$

The last step is to divide the total by $n.$

$\text{Mean}=\cfrac{\text{total}}{n}=\cfrac{1300}{30}=43.333… = 43.3 \ \text{(to the nearest tenth)}$

But remember that this is an estimate for the mean.

The estimated mean is $43.3 \, g.$

Teaching tips for mean from a frequency table

Providing students with worksheets of practice problems is an easy way for them to practice finding the mean from a frequency table using given data values.

Have students write step-by-step instructions in their math notebook while following example problems. You can also display the examples and instructions on an anchor chart that is displayed in the classroom for easy reference.

Incorporate technology into the skill by allowing students to use Microsoft Excel or Google sheets to find formulas to find the mean.

Easy mistakes to make

Finding median or mode instead of finding mean
Check if you have been asked for the median, mode or mean average.

Not dividing by the total frequency
Remember to divide by the total frequency, not by the number of rows in the table. Always check to see if your final answer is sensible.

Thinking the mean must be a whole number
The mean does not have to be a whole number; it can also be a decimal or a fraction.

Always estimating the mean from all frequency tables
You only use the estimated mean when you have a grouped frequency table because you do not have the actual values for the data.

Thinking a frequency table is different from a frequency distribution table
A frequency distribution table is the same as a frequency table.

Practice mean from a frequency table questions

1.26

1

2

1.27

You need to multiply the numbers by the frequencies and find the total. Then divide the total by $n,$ the frequency total,

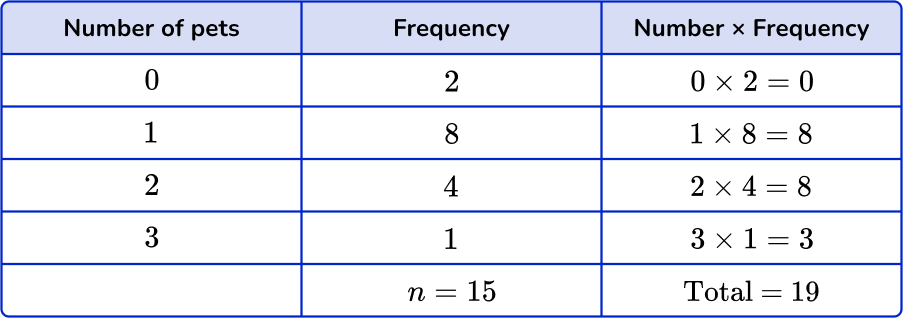
Mean from frequency table Image 26 US

$\text{Mean}=\cfrac{\text{total}}{n}=\cfrac{19}{15}=1.2666… = 1.27 \ \text{(to nearest hundredth)}$

6.71

6.72

6

7

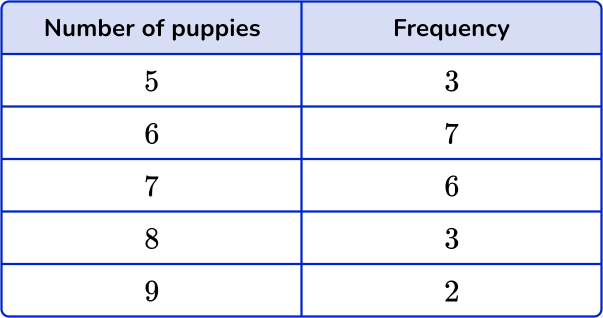
You need to multiply the numbers by the frequencies and find the total. Then divide the total by $n,$ the frequency total.

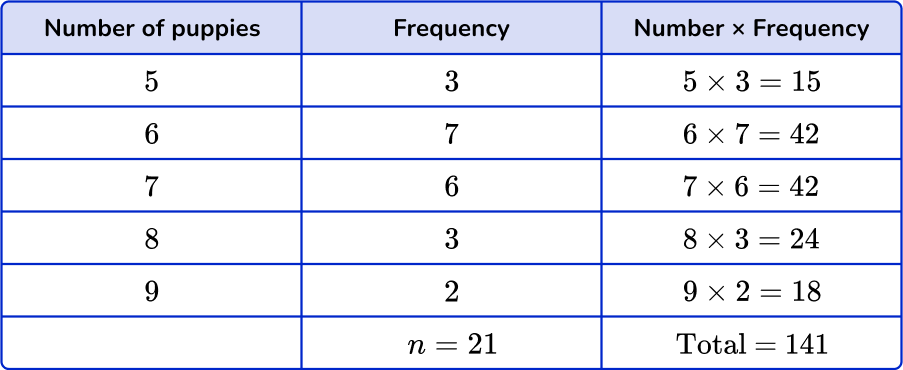
Mean from frequency table Image 28 US

$\text{Mean}=\cfrac{\text{total}}{n}=\cfrac{141}{21}=6.714… = 6.71 \ \text{(to nearest hundredth)}$

59.9

60

59.8

59

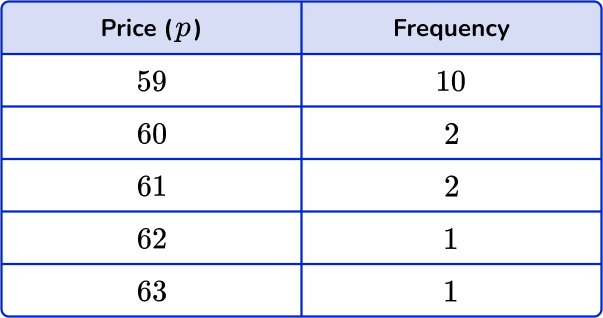
You need to multiply the numbers by the frequencies and find the total. Then divide the total by $n,$ the frequency total.

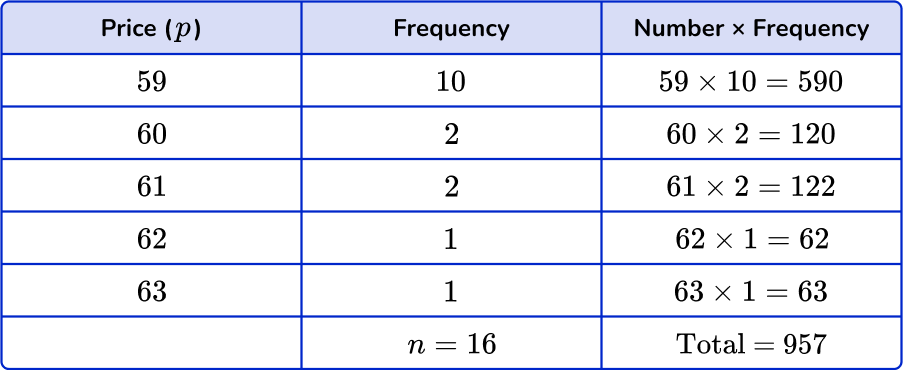
Mean from frequency table Image 30 US

$\text{Mean}=\cfrac{\text{total}}{n}=\cfrac{957}{16}=59.81… = 59.8 \ \text{(to nearest tenth)}$

3.11

3.12

0-2

3

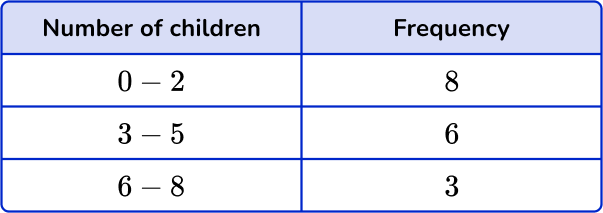
You need to use midpoints. Multiply the midpoints by the frequencies and find the total. Then divide the total by $n,$ the frequency total.

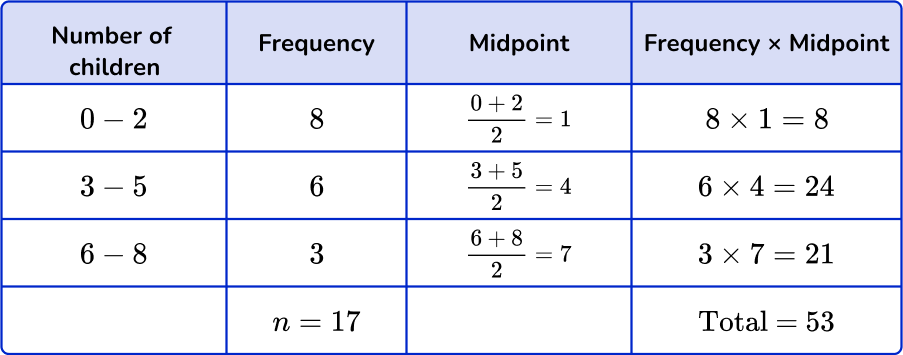
Mean from frequency table Image 32.1 US

$\text{mean}=\cfrac{\text{total}}{n}=\cfrac{53}{17}=3.117… = 3.12 \ \text{(to nearest hundredth)}$

51.2

51.3

65.5

55.5

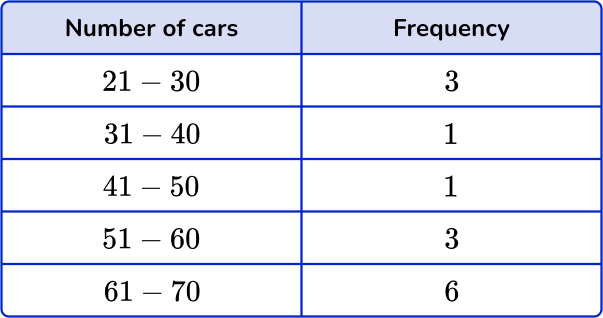
You need to use midpoints. Multiply the midpoints by the frequencies and find the total. Then divide the total by $n,$ the frequency total.

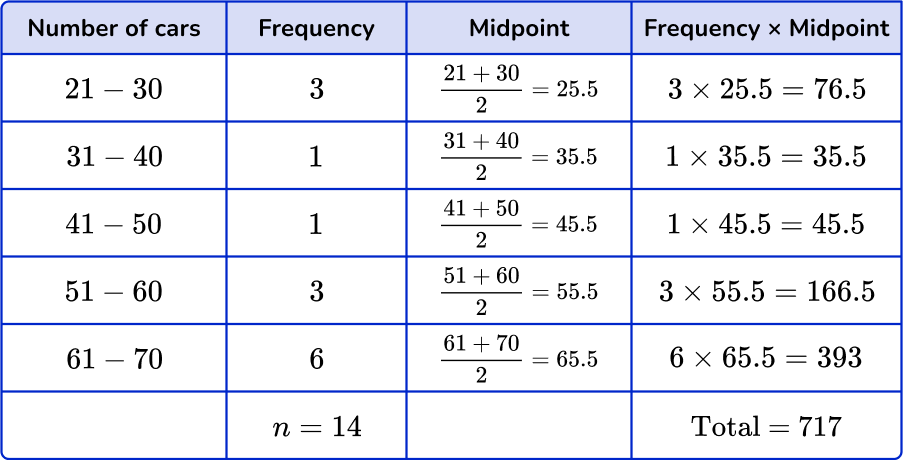
Mean from frequency table Image 34.1 US

$\text{Mean}=\cfrac{\text{total}}{n}=\cfrac{717}{14}=51.214… = 51.2 \ \text{(to nearest tenth)}$

3.41

3.75

3.42

$3.5$ to $4$

You need to use midpoints. Multiply the midpoints by the frequencies and find the total. Then divide the total by $n,$ the frequency total.

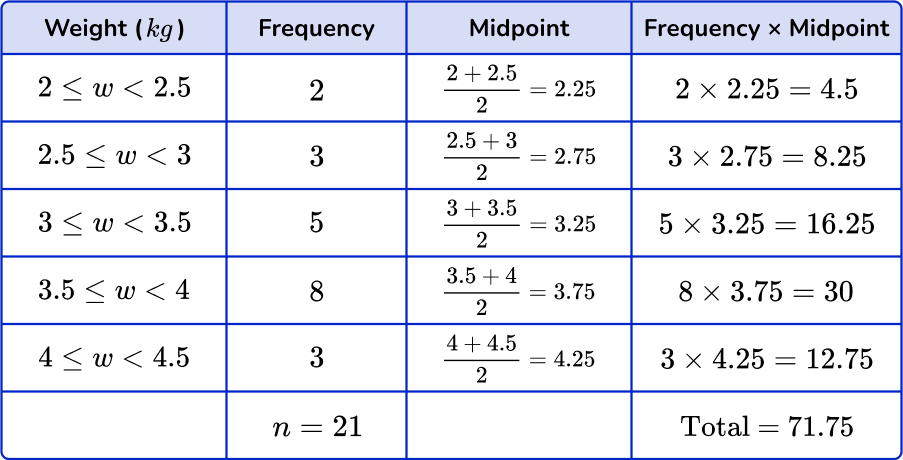
Mean from frequency table Image 36 US

$\text{Mean}=\cfrac{\text{total}}{n}=\cfrac{71.75}{21}=3.4166… = 3.42 \ \text{(to nearest hundredth)}$

Mean from frequency table FAQs

Is a frequency table a type of graph?

While a frequency table is not a type of graph, the data that is recorded within a frequency table can be used to create graphs, including box plots, histograms, stem-and-leaf plots, dot plots, and many more.

What is the difference between grouped data and ungrouped data?

Grouped data is when the data is given in the form of class intervals, such as $0 \text{-}5, 6 \text{-}10,$ etc. Ungrouped data refers to when the data is given as individual data points or values.

What are class intervals?

Class intervals are the organized groups of the numerical data. They can have the same or different class widths, but must not overlap.

What is the standard deviation?

The standard deviation is a value that summarizes the variation around the mean. It is another measure that can be calculated from the data in frequency tables.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.