FREE DOWNLOAD
Surface Area Of A Triangular Prism Worksheet
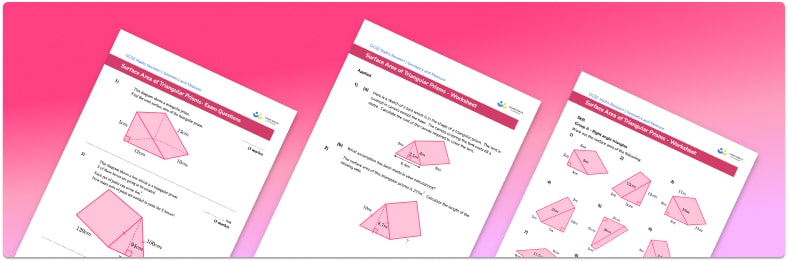
Help your students prepare for their Maths GCSE with this free surface area of a triangular prism worksheet of 34 questions and answers
- Section 1 of the surface area of a triangular prism worksheet contains 27 skills-based surface area of spheres questions, in 3 groups to support differentiation
- Section 2 contains 4 applied surface area of a triangular prism questions with a mix of worded problems and deeper problem solving questions
- Section 3 contains 3 foundation and higher level GCSE exam style surface area of a triangular prism questions
- An answer key and a mark scheme for all surface area of a triangular prism questions are provided
- Questions follow variation theory with plenty of opportunities for students to work independently at their own level
- All questions created by fully qualified expert secondary maths teachers
Suitable for GCSE maths revision for AQA, OCR and Edexcel exam boards
Unlock access to download your free resource
You can unsubscribe at any time (each email we send will contain an easy way to unsubscribe). To find out more about how we use your data, see our privacy policy.
Raise maths attainment across your school with hundreds of flexible and easy to use GCSE maths worksheets and lessons designed by teachers for teachers.
Surface area of a triangular prism at a glance
Surface area is a measure of the total area of all of the faces of a solid shape. A triangular prism is a 3D shape with identical triangles at each end, connected by a number of rectangular faces (lateral faces). To find the total surface area of a triangular prism, we find the area of each face and add them together.
A triangular prism has five faces. When finding the surface area of the triangular prism, we start by finding the area of the triangular faces. Remember that to find the area of a triangle, we multiply the base of the triangle by the height of the triangle and divide by two. The triangular ends are exactly the same (congruent) so their areas will be identical.
We can then find the lateral surface area (the area of the rectangular sides). Note that each rectangular face may have a different area, depending on its side lengths. The total surface area can be found by calculating the sum of the areas of the triangular faces, area of the base and area of the top faces.
The depth of a prism can also be referred to as the length or the height of the prism depending on its orientation.
Surface area of 3D shapes is measured in square units such as cm^2 or mm^2 .
Looking forward, students can then progress to additional surface area worksheets and other geometry worksheets, for example a simplifying expressions worksheet or simultaneous equations worksheet.
For more teaching and learning support on Geometry our GCSE maths lessons provide step by step support for all GCSE maths concepts.
Do you have students who need additional support?
With Third Space Learning's secondary maths tutoring programmes, students in Year 7-11 receive regular one to one maths tutoring to address gaps, build confidence and boost progress.
"My confidence in the tutoring is high. We've had some phenomenal results. I even had one girl get a Grade 8 this year; she came to every tutoring session."
Stacey Atkins, Maths Director, Outwood Grange Academies Trust