One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Arithmetic Squares and square roots Cubes and cube roots BIDMASThis topic is relevant for:

To The Power Of
Here we will learn about powers, raising numbers to the power of, and writing expressions in index form.
There are also to the power of worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is meant by to the power of?
To the power of is used to describe a number raised to a power.
For example,
- We can write 3 \times 3 in a shorter way, using exponents 3^{2}.
We can say this as 3 to the power of 2.
- We can write -2 \times -2 \times -2 in a shorter way, using exponents -2^{3}.
We can say this as -2 to the power of 3.
- We can write \frac{1}{5} \times \frac{1}{5} \times \frac{1}{5} \times \frac{1}{5} in a shorter way, using exponents \frac{1}{5}^{4}.
We can say this as \frac{1}{5} to the power of 4.
This is known as index notation or index form and features heavily in scientific notation. To write a number in index form we have a base number raised to a power. The base number can be an integer, decimal, fraction, etc. and the power tells us the number of times we multiply the base number.
For example,
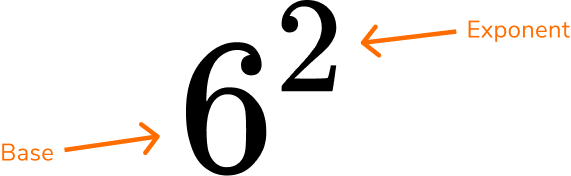
The number 6 is called the base, and the number 2 is the exponent (or power).
In words, 6^2 can be written as “ 6 to the power of 2 ” or “ 6 to the second power”, or “ 6 squared”.
We can multiply a number by itself as many times as we want using powers.
What is meant by to the power of?

How to describe powers
In order to describe powers with words:
- Identify the base number.
- Consider the index (or power).
- Work out the answer.
Explain how to describe powers

Powers and roots worksheet (including to the power of)

Get your free to the power of worksheet of 20+ powers and roots questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Powers and roots worksheet (including to the power of)

Get your free to the power of worksheet of 20+ powers and roots questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on powers and roots
To the power of is part of our series of lessons to support revision on powers and roots. You may find it helpful to start with the main powers and roots lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
To the power of examples
Example 1: describing powers
Describe the expression 11 \times 11 \times 11 \times 11.
- Identify the base number.
The base number is 11.
2Consider the index (or power).
11 is being multiplied by itself 4 times. So the power will be 4.
3Work out the answer.
11 to the power of 4, or 11 to the fourth power.
Example 2: describing powers
Describe the expression 7^{3}.
Identify the base number.
The base number is 7.
Consider the index (or power).
The index (or power) is 3. \ 7 is being multiplied by itself 3 times.
Work out the answer.
7 to the power of 3 or 3 to the third power.
Example 3: evaluating powers
Evaluate 2^{4}.
Identify the base number.
The base number is 2.
Consider the index (or power).
The index (or power) is 4.
Work out the answer.
Example 4: evaluating powers
Evaluate 3^{5}.
Identify the base number.
The base number is 3.
Consider the index (or power).
The index (or power) is 5.
Work out the answer.
Example 5: expressing in index form
Write 9 \times 9 \times 9 \times 9 \times 9 in index form.
Identify the base number.
There is one base number, 9.
Consider the index (or power).
9 is multiplied by itself 5 times, the index is 5.
Work out the answer.
Example 6: expressing in index form
Write 5 \times 3 \times 5 \times 3 \times 5 in index form.
Identify the base number.
There are two base numbers, 3 and 5.
Consider the index (or power).
3 is multiplied by itself 2 times, its index is 2.
5 is multiplied by itself 3 times, its index is 3.
Work out the answer.
Common misconceptions
- The power is what we multiply the number by
The power tells us how many times to multiply the base number by itself.
For example,
4^2=4 \times 4=16 not 4 \times 2=8.
- Mixed bases in index form
Mixed bases in multiplication expressions require a power per base number when written in index form.
For example,
5 \times 0.5 \times 5 \times 5 \times 0.5 \times 5=0.5^2 \times 5^4
- Power of \bf{1}
A key fact to remember is that every number has a secret power of 1, we can’t see it, but we have to remember it’s there.
For example,
\begin{aligned} &8=8^1 \\\\ &80=80^1 \\\\ &800=800^1 \\\\ &\frac{1}{8}=\left(\frac{1}{8}\right)^1 \\\\ &1.8=1.8^1 \end{aligned}
Practice to the power of questions
1. Evaluate 5^{2}.



5 to the power of 2

2. Write 2 \times 7 \times 7 \times 2 \times 7 \times 7 in index form.




There are two base numbers, 2 and 7.
2 is multiplied by itself 2 times, it has a power of 2.
7 is multiplied by itself 4 times, it has a power of 4.
2 \times 7 \times 7 \times 2 \times 7 \times 7=2^2 \times 7^4
3. Evaluate 4^{4}.



4 to the power of 4

4. Describe the expression 5^{7}.
5 to the power of 7


7 to the power of 5


The base number is 5.
The power is 7.
Hence, 5 to the power of 7.
5. Write 0.3 \times 3 \times 0.3 \times 0.3 \times 0.3 in index form.




There are two base numbers, 0.3 and 3.
0.3 is multiplied by itself 4 times, it has a power of 4.
3 is multiplied by itself 1 times, it has a power of 1.
0.3 \times 3 \times 0.3 \times 0.3 \times 0.3=0.3^4 \times 3
6. Describe the expression 7^{3}.


7 to the power of 3

3 to the power of 7

The base number is 7.
The power is 3.
Hence, 7 to the power of 3.
The power of GCSE questions
1. Evaluate 8^4.
(1 mark)
(1)
2. Write 4 \times 6 \times 6 \times 4 \times 4 \times 5 in index form.
(1 mark)
(1)
3. Simplify \frac{3 \times 3\times 3\times 3}{4\times 4}.
(2 marks)
Evaluating the numerator 3\times 3 \times 3 \times 3=3^{4}=81
or evaluating the denominator 4 \times 4 =4^{2}=16.
(1)
Writing the resulting quotient \frac{3^{4}}{4^{2}}.
(1)
Learning checklist
You have now learned how to:
- Describe numbers to the power of
- Identify special powers
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.