GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
Square numbers and square roots Cube numbers and cube roots BIDMAS Fractions Negative numbers Standard form / scientific notationThis topic is relevant for:

Negative Powers
Here we will learn about negative powers, including what they are, how to simplify and evaluate them, and how to combine them with other laws of exponents.
There are also powers and roots worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are negative powers?
Negative powers are a type of index that represents a number that can be written as a fraction.
For example,
3^{-2}=\frac{1}{3^{2}}=\frac{1}{9} .
A negative power does not mean that the base is a negative number.
If the base is a positive number, the denominator of the fraction remains positive.
Let’s see why a negative power is a fraction using the powers of 10 .

As we divide each row by 10 , the power is reduced by 1 .
When we reach 100 (the zero exponent) we are dividing the base number by itself, any base to the power of 0 is always equal to 1 .
When we divide by a further 10 , we get 0.1=\frac{1}{10}=10^{-1} .
As we continue to divide by 10 , the denominator of the fraction becomes increasingly large, meaning that the original number gets smaller and smaller (closer to 0 ).
What are negative powers?

Positive reciprocal
Another term for the negative power is the positive reciprocal.
The reciprocal of a number is the value that can be multiplied by the original number to get the answer of 1 .
For example,
2\times\frac{1}{2}=1 and so \frac{1}{2} is the positive reciprocal of 2 .
Introducing a negative power, we get 2^{-1}=\frac{1}{2^{1}}=\frac{1}{2} which we can express in a general form as
x^{-a}=\frac{1}{x^{a}}
where x and a are constants.
Most of the laws of indices can include a negative power and the toughest questions usually involve a fractional base number raised to a negative fraction.
For example,
(\frac{25}{4})^{-\frac{3}{2}}=\frac{8}{125} .
Simplify and evaluate
Questions will often require you to simplify or evaluate an expression.
These terms are subtly different and so the table below shows a couple of examples of the difference between them.
| Simplify (2^{2})^{-3} | Evaluate (2^{2})^{-3} |
|---|---|
| Simplify: to make something easier to understand. | Evaluate: to find the value of an expression. |
| (2^{2})^{-3}=2^{2\times -3}=2^{-6} | …=\frac{1}{2^{6}}=\frac{1}{64} |
| So (2^{2})^{-3}=2^{-6} as 2^{-6} is more simple to understand… | … but the value of the expression (2^{2})^{-3}=\frac{1}{64} . |
Remember: A fraction can also be converted to a decimal.
How to operate with negative powers
In order to use negative powers:
- Simplify any powers using laws of indices.
- Evaluate or solve (if required).
How to operate with negative powers

Powers and roots worksheet (includes negative powers)

Get your free negative powers worksheet of 20+ powers and roots questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Powers and roots worksheet (includes negative powers)

Get your free negative powers worksheet of 20+ powers and roots questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on powers and roots
Negative powers is part of our series of lessons to support revision on powers and roots. You may find it helpful to start with the main powers and roots lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Negative powers examples
Example 1: simplify and evaluate
Simplify and evaluate the expression.
6^{-2}\div 6^{-4}- Simplify any powers using laws of indices.
As x^{a}\div x^{b}=x^{a-b} , we have 6^{-2}\div 6^{-4} = 6^{-2--4}=6^{-2+4}=6^{2} .
2Evaluate or solve (if required).
Evaluating the expression 6^{2} , we get 6^{2}=6\times 6=36.
So 6^{-2}\div 6^{-4}=36 .
Example 2: algebraic terms
Write the following expression as a fraction in its simplest form.
2y^{-a}\times 2x^{b}Simplify any powers using laws of indices.
The bases are different for each term in the expression and so we have to treat each term separately.
2y^{-a}=2\times{y^{-a}}=2\times{\frac{1}{y^{a}}}=\frac{2}{y^a}2x^{b} does not require any simplifying at this stage.
Now let’s multiply these terms together.
2y^{-a}\times{2x^{b}}=\frac{2}{y^{a}}\times{2x^{b}}=\frac{2\times{2x^{b}}}{y^{a}}=\frac{4x^{b}}{y^{a}}Evaluate or solve (if required).
As this is an algebraic expression with no values for x, y, a, or b , we cannot evaluate this expression.
The solution is therefore 2y^{-a}\times{2x^{b}}=\frac{4x^{b}}{y^{a}} .
Example 3: inequalities
Solve the inequality.
(3x)^{-2}<\frac{1}{36}Simplify any powers using laws of indices.
Looking at the left hand side of the inequality sign, we have 3x being raised to the power of -2 and so we can write this as (3x)^{-2}=\frac{1}{(3x)^{2}}=\frac{1}{3^{2}x^{2}}=\frac{1}{9x^{2}}
So we now have the inequality \frac{1}{9x^{2}}<\frac{1}{36} .
Evaluate or solve (if required).
Multiplying both sides by 9x^{2} , we get 1<\frac{9x^{2}}{36} which can be simplified by dividing the numerator and the denominator by 9 , 1<\frac{x^{2}}{4} . Note that we can multiply both sides by 9x^{2} without worrying about the direction of the inequality symbol because 9x^{2} is always positive. More complicated fractional inequalities are looked at in A level Further Maths.
Multiplying each side by 4 , we get 4<x^{2} . Which is the same as x^{2}>4 .
Calculating the square root of both sides of the inequality symbol, we obtain the solutions, x<-2 and x>2 .
Remember: -2\times -2=4 and so any value less than -2 will be larger than 4 (-3\times -3=9, -10\times -10=100 etc). This is the same as for any value larger than 2 .
Example 4: negative fractional power
Simplify and evaluate the following expression.
125^{-\frac{2}{3}}Simplify any powers using laws of indices.
As the power of 125 is a fraction, and a negative number, we are going to simplify the base by looking at the denominator of the power first. As the denominator of the fraction is the nth root of the base number.
125^{-\frac{2}{3}}=(125^{\frac{1}{3}})^{-2}=(\sqrt[3]{125})^{-2}=5^{-2}Remember: Raising a term to the power of \frac{1}{3} is exactly the same as the cube root.
Now we can look at the negative aspect of the power, 5^{-2}=\frac{1}{5^{2}} .
Evaluate or solve (if required).
The expression \frac{1}{5^{2}} is the simplified form of the expression, but we can now evaluate the expression as we know that 5^{2}=25 so \frac{1}{5^{2}}=\frac{1}{25} .
So the solution is \frac{1}{25} .
Example 5: fractional base number
Simplify fully, (\frac{3}{4})^{-3} .
Write your answer as a mixed number.
Simplify any powers using laws of indices.
As we start with a base of \frac{3}{4} that is raised to the power of -3 , we know that the negative power produces the positive reciprocal of the base (remember that the reciprocal is the number you multiply by to get the answer 1 ).
So what do we need to multiply \frac{3}{4} by, to get the value of 1 ?
1\div{\frac{3}{4}}=1\times{\frac{4}{3}}=\frac{4}{3}So as \frac{3}{4}\times{\frac{4}{3}}=\frac{12}{12}=12\div{12}=1 , the reciprocal of \frac{3}{4} is \frac{4}{3} .
So we can now say (\frac{3}{4})^{-3}=(\frac{4}{3})^{3}=\frac{4^{3}}{3^{3}} .
Evaluate or solve (if required).
Looking at the power of the numerator and denominators separately, we have 4^{3}=4\times 4\times 4=64 .
3^{3}=3\times 3\times 3=27 and so \frac{4^{3}}{3^{3}}=\frac{64}{27}=2\frac{10}{27} .
Example 6: expressing a power with a different base
Simplify fully, (4^{-10})^{\frac{1}{2}} .
Write your answer as a power of 2 .
Simplify any powers using laws of indices.
The law of indices we are going to use involves parentheses, namely
(x^{a})^{b}=x^{a\times b} , we get (4^{-10})^{\frac{1}{2}}=4^{-10\times{\frac{1}{2}}}=4^{-5} .
Evaluate or solve (if required).
The question does not want us to state the value of \frac{1}{4^{5}} . Instead, the question asks for the solution to be written as a power of 2 , so we need to change the expression so that the base number is 2 , instead of 4 .
As 4=2^{2} , we have 4^{-5}=(2^{2})^{-5}=2^{2\times{-5}}=2^{-10} .
So the solution is 2^{-10} .
Common misconceptions
- Negative powers and negative number
A common error is to think that a negative power suggests that the entire number is a negative number. This is incorrect because a negative power means that we are finding a positive reciprocal of the base.
For example,
2^{-4}=-2^{4}=-16 is incorrect.
The correct answer is 2^{-4}=\frac{1}{2^{4}}=\frac{1}{16} .
- Changing the base incorrectly
For example,
5^{3}\times2^{-4}=(5\times{2})^{3-4}=10^{-1}=\frac{1}{10} .
This is incorrect as the bases must be the same when simplifying calculations with powers.
The correct answer would be 5^{3}\times{2^{-4}}=5^{3}\times{\frac{1}{16}}=\frac{125}{16} .
- Subtracting a negative number
A common error is to incorrectly subtract negative numbers.
For example,
3^{-2}\div{3^{-5}}=3^{-2-5}=3^{-7}=\frac{1}{3^{7}}This is incorrect because the 5 is a negative number, and subtracting a negative number means that we add.
The correct answer would be 3^{-2}\div 3^{-5}=3^{-2--5}=3^{-2+5}=3^{3}=27.
- BIDMAS
When raising a base to a power, the power is associated with a variable or an expression.
For example, let’s look at 3x^{-2}.
Using BIDMAS we can see that, x is being raised to the power of -2 , and then is multiplied by 3 to get the answer \frac{3}{x^{2}} .
However a common error is to calculate 3x raised to the power of -2 , giving the answer \frac{1}{9x^{2}} which is incorrect. If this was the case, the question would be written as (3x)^{-2}.
- Incorrect application of the exponent
A similar circumstance is applied to fractions that are raised to a power.
For example, let’s look at (\frac{5}{2})^{-3} .
The correct application of the laws of indices would give a correct answer of
(\frac{5}{2})^{-3}=(\frac{2}{5})^{3}=\frac{8}{125} .
However a common error would be to apply the -3 only to the numerator, leaving the denominator unchanged. This would give the incorrect answer of
(\frac{5}{2})^{-3}=\frac{1}{125}\times\frac{1}{2}=\frac{1}{250} .
Practice negative powers questions
1. Evaluate 5^{4}\times 5^{-6} .




2. Simplify 3x^{a}\div 6^{y-b} fully.




=3x^{a}\times{\frac{y^{b}}{6}}=\frac{3x^{a}y^{b}}{6}=\frac{x^{a}y^{b}}{2}
3. State the range of values for the following inequality, x^{-2}>\frac{1}{16} .




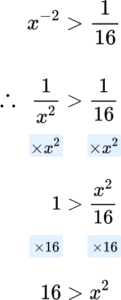
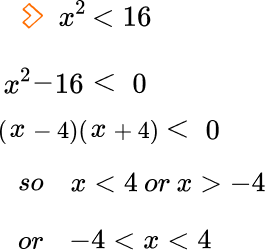
4. Evaluate 16^{\frac{-3}{4}} .





5. Evaluate (\frac{1}{5})^{-2} .




6. Simplify the expression below. Write your answer in the form 2^{n} .
(8^{2})^{-\frac{1}{3}}




Negative powers GCSE questions
1. Order the numbers smallest to largest.
6\times 10^{-4} , 0.006\times 10^{5} , 6\times 10^{0} , 10^{-4}\times 2^{3} , 0.06\times 10^{1}
(3 marks)
3 correct answers.
(1)
4 correct answers.
(2)
All 5 correct answers.
(3)
2. (a) Solve x^{-3}=\frac{1}{125} .
(b) Solve the inequality x^{-2}>16 .
(6 marks)
(a)
x^{-3}=\frac{1}{x^{3}}(1)
x^{3}=125(1)
x=5(1)
(b)
x^{-2}>\frac{1}{x^{2}}(1)
x^{2}>\frac{1}{16}(1)
x<-\frac{1}{4} or x>\frac{1}{4}
(1)
3. Use laws of indices to simplify and evaluate
\frac{7^{5}\times{7^{-2}}}{7^{6}} .
(3 marks)
(1)
7^{3}\div 7^{6}=7^{3-6}=7^{-3}(1)
7^{-3}=\frac{1}{7^{3}}=\frac{1}{343}(1)
Learning checklist
You have now learned how to:
-
Extend your understanding of the number system to include powers
-
Calculate with roots, and with integer indices
-
Simplify expressions involving sums, products and powers, including the laws of indices
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.