Surface area of a cuboid

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Area of a rectangle 3D shapes Faces, edges and vertices Decimals

This topic is relevant for:

GCSE Maths Geometry and Measure 3D Shapes Cuboid

Surface Area Of A Cuboid

Here we will learn about the surface area of a cuboid and how to calculate it.

There are also volume and surface area of a cuboid worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the surface area of a cuboid?

The surface area of a cuboid is the total area of all of the faces of a cuboid (or rectangular prism).

The $3$ dimensions of a cuboid are width, length and height.

Cuboids have three pairs of identical faces – top and bottom, front and back, and left and right.

To work out the total surface area of a cuboid, we need to work out the area of each rectangular face and add them all together.

E.g. Find the surface area of a cuboid.

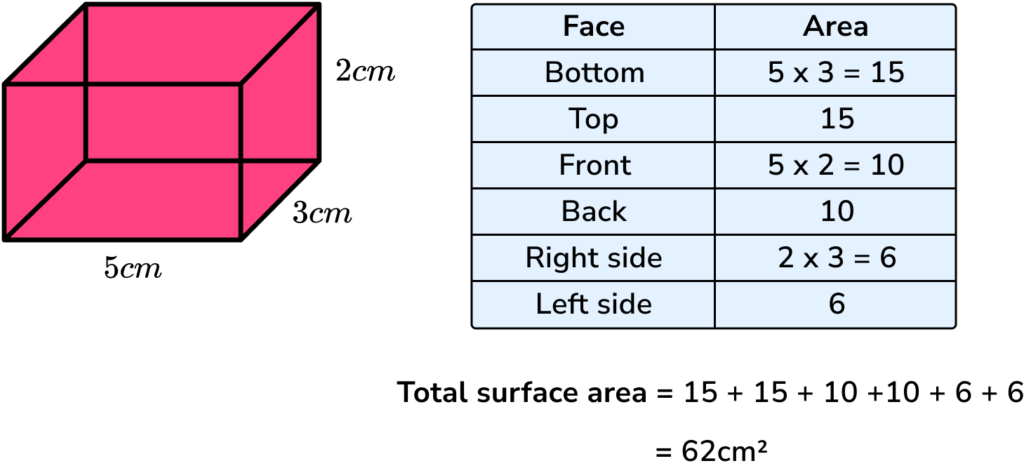
Since it is an area, surface area is measured in square units (e.g. $mm^2, cm^2, m^2$ etc).

What is the surface area of a cuboid?

How to calculate the surface area of a cuboid

In order to work out the surface area of a cuboid:

Work out the area of each face.
Add the six areas together.
Include the units.

How to calculate the surface area of a cuboid

Surface area of a cuboid worksheet

Get your free surface area of a cuboid worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Surface area of a cuboid worksheet

Get your free surface area of a cuboid worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Surface area of a cuboid examples

Example 1: surface area of a cuboid

Work out the surface area of the cuboid

Work out the area of each face.

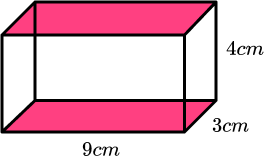
The area of the bottom is $9\times3=27cm^2$ .

The top face is the same as the bottom face so the area of the top is also $27cm^2$ .

The area of the front is $9\times4=36cm^2$ .

The back face is the same as the front face so the area of the back is also $36cm^2$ .

The area of the right hand side is $3\times4=12cm^2$ .

The left side face is the same as the right side face so the area of the left side is also $12cm^2$ .

It will make our working clearer if we use a table:

Face	Area
Bottom	9×3=27
Top	27
Front	9×4=36
Back	36
Right side	3×4=12
Left side	12

2Add the six areas together.

The sum of the areas is: $27+27+36+36+12+12=150$

3Include the units.

The measurements on the cuboid are in cm therefore the total surface area of the cuboid = $150cm^2$ .

Example 2: surface area of a cuboid

Work out the surface area of the cuboid

Work out the area of each face.

Face	Area
Bottom	6×3=18
Top	18
Front	9×6=54
Back	54
Right side	9×3=27
Left side	27

Add the six areas together.

18+18+54+54+27+27=198

Include the units.

The measurements on the cuboid are in $mm$ therefore the total surface area of the cuboid = $198mm^2$ .

Example 3: surface area of a cube

Work out the surface area of this cube

Work out the area of each face.

Each face of a cube is the same. For this cube, the area of each face is $8\times8=64cm^2$

Add the six areas together.

6\times64=384

Include the units.

The measurements on the cube are in $cm$ therefore the total surface area of the cube = $384cm^2$ .

Example 4: surface area with different units

Work out the surface area of this cuboid

Work out the area of each face.

Notice that one of the measurements is in metres and the rest are in centimetres. Before we can calculate any areas, we need to ensure all units are the same. In this case, $0.1m=10cm$ so we can use $10cm$ .

Face	Area
Bottom	8×10=80
Top	80
Front	8×2.5=20
Back	20
Right side	10×2.5=25
Left side	25

Add the six areas together.

80+80+20+20+25+25=250

Include the units.

The measurements we have used are in cm therefore the total surface area = $250cm^2$ .

Example 5: surface area using algebra

Work out the surface area of this cuboid.

Work out the area of each face.

Face	Area
Bottom	14×x=14x
Top	14x
Front	14×6=84
Back	84
Right side	6×x=6x
Left side	6x

Add the six areas together.

14x+14x+84+84+6x+6x = 40x+168

Include the units.

The measurements we have used are in cm therefore the total surface area = $(40x+168) cm^2$ .

If we are told the value of the surface area, we can use the expression we have found to work out the value of $x$ .

Let’s say the surface area of this cuboid is $328cm^2$ . Then we can say:

$40x+168=328$ .

Now we can solve this equation:

40x+168=328

40x=160

x=4cm

The width of this cuboid is $4cm$ .

Example 6: surface area using algebra

Work out the surface area of this cuboid

Work out the area of each face.

Face	Area
Bottom	10×4y=40y
Top	40y
Front	10×2y=20y
Back	20y
Right side	2y×4y=8y²
Left side	8y²

Add the six areas together.

40y+40y+20y+20y+8y^2+8y^2= 16y^2+120y

Include the units.

The measurements we have used are in $m$ therefore the total surface area = $(16y^2+120y) m^2$ .

Common misconceptions

Calculating volume instead of surface area

Volume and surface area are different things – volume is the space within the shape whereas surface area is the total area of the faces. To find surface area, we need to work out the area of each face and add them together.

Equal faces

A common mistake is to think that four of the faces are equal.

E.g.
The first pair of faces are equal to each other.
The second pair of faces are equal to each other.
The third pair of faces are equal to each other.

Surface area of a cuboid is part of our series of lessons to support revision on cuboid. You may find it helpful to start with the main cuboid lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Practice surface area of a cuboid questions

315\mathrm{cm}^{2}

222\mathrm{cm}^{2}

342\mathrm{cm}^{2}

462\mathrm{cm}^{2}

Work out the area of each of the six faces:

Face	Area
Bottom	7×15=105
Top	105
Front	3×15=45
Back	45
Right side	3×7=21
Left side	21

$\text{Total surface area: }105+105+45+45+21+21=342\mathrm{cm}^{2}$

96\mathrm{cm}^{2}

64\mathrm{cm}^{2}

24\mathrm{cm}^{2}

256\mathrm{cm}^{2}

Since it is a cube, all of the faces are the same. The area of each face is $4\times 4=16\mathrm{cm}^{2}$ . There are six identical faces therefore the total surface area of the cube is $6 \times 16=96 \mathrm{cm}^{2}$

33.56\mathrm{cm}^{2}

4.2\mathrm{cm}^{2}

8900\mathrm{cm}^{2}

12400\mathrm{cm}^{2}

Some of the measurements are in m and one is in cm. We need all of the measurements to be in the same units so convert the metres to centimetres. $0.7m=70cm$ and $0.4m=40cm$ . Now we can calculate the areas:

Face	Area
Bottom	70×15=1050
Top	1050
Front	70×40=2800
Back	2800
Right side	40×15=600
Left side	600

\text{Total surface area: } 1050+1050+2800+2800+600+600=8900\mathrm{cm}^{2}

16a \mathrm{cm}^{2}

15a \mathrm{cm}^{2}

(20a+30) \mathrm{cm}^{2}

(16a+30) \mathrm{cm}^{2}

Work out the area of each of the six faces:

Face	Area
Bottom	5×a=5a
Top	5a
Front	3×a=3a
Back	3a
Right side	3×5=15
Left side	15

\text{Total surface area: } 5a+5a+3a+3a+15+15=(16a+30) \mathrm{cm}^{2}

80b \mathrm{mm}^{2}

16b^{2} \mathrm{mm}^{2}

(4b^{2}+48b) \mathrm{mm}^{2}

(8b^{2}+16b) \mathrm{mm}^{2}

Work out the area of each of the six faces:

Face	Area
Bottom	8×b=8b
Top	8b
Front	b×2b=2b2
Back	2b2
Right side	8×2b=16b
Left side	16b

\text{Total surface area: }8b+8b+2b^{2}+2b^{2}+16b+16b=(4b^{2}+48b)mm^{2}

6.76cm

5cm

14.2cm

20.29cm

Work out the area of each of the six faces:

Face	Area
Bottom	7×x=7x
Top	7x
Front	3×x=3x
Back	3x
Right side	3×7=21
Left side	21

\text{Total surface area: }7x+7x+3x+3x+21+21=20x+42

Since we know the surface area is $142\mathrm{cm}^{2}$
we can say:
$20x+42=142\\ 20x=100\\ x=5\mathrm{cm}$

Surface area of a cuboid GCSE questions

1. Calculate the surface area of the cuboid.

(3 marks)

Show answer

Two of:
$12\times 3.5=42\\ 12\times 4=48\\ 4\times 3.5=14$

(1)

42+42+48+48+14+14

(1)

208\mathrm{cm}^{2}

(1)

2. A breakfast cereal producer wants to produce a cereal box with a volume of $4800cm^3$ . The company wants to use as little cardboard as possible for each box. Should they use box $A$ or box $B$ ? You must show your working.

(5 marks)

Show answer

Box $A$ surface area: $160+160+600+600+240+240$

(1)

\text{Surface area }=2000\mathrm{cm}^{2}

(1)

Box $B$ surface area: $192+192+480+480+250+250$

(1)

\text{Surface area }=1844\mathrm{cm}^{2}

(1)

They should use box $B$

(1)

3. John wants to paint $4$ identical doors, as shown below.

$1$ litre of paint will cover
$10\mathrm{m}^{2}$
John has $1$ litre of paint. Does he have enough paint to cover all $4$ doors? You must show your working.

(5 marks)

Show answer

5cm = 0.05m

(1)

Surface area of $1$ door: $0.03+0.03+1.2+1.2+0.1+0.1$

(1)

\text{Surface area of 1 door }=2.66\mathrm{m}^{2}

(1)

\text{Surface area of 4 doors: }4 \times 2.66=10.64\mathrm{m}^{2}

(1)

No he does not have enough paint

(1)

Learning checklist

You have now learned how to:

Calculate the surface area of a cuboid

Use the properties of faces, surfaces, edges and vertices of cubes and cuboids to solve problems in 3D

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.