High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Converting fractions decimals and percentages Fractions Decimals Integers ProbabilitySample space
Here you will learn about sample space, including what it is and how to use it to find probabilities.
Students will first learn about sample space as part of 7 th grade in statistics and probability and continue to learn about it in high school.
What is a sample space?
A sample space is a list, diagram or table of values used to display the set of all possible outcomes.
To create a sample space diagram, think about the possible outcomes of a situation.
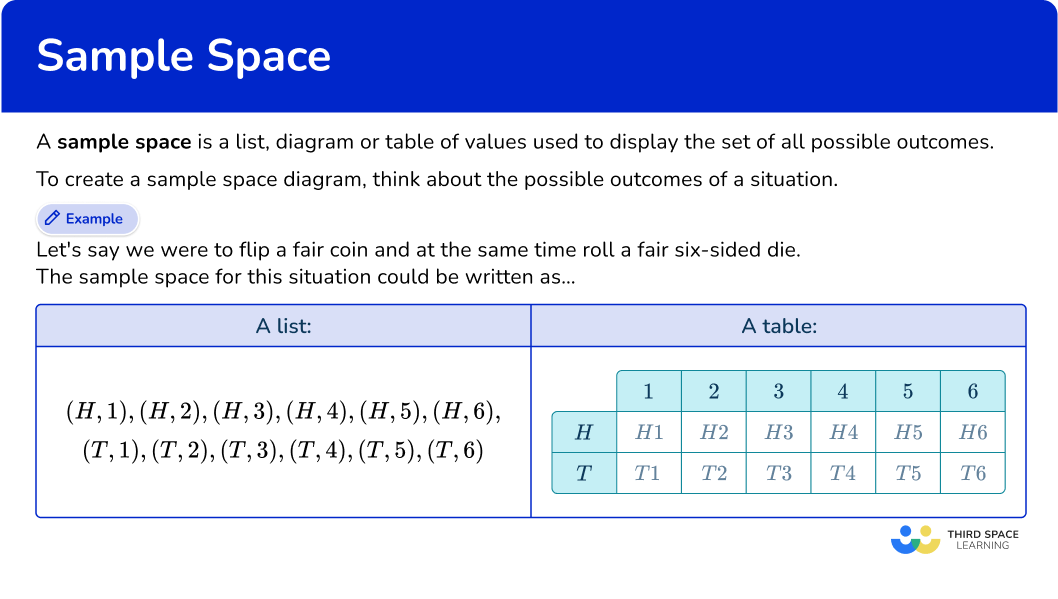
For example,
Let’s say you were to flip a fair coin with outcomes H (heads) or T (tails) and at the same time roll a fair six-sided die with outcomes: 1, 2, 3, 4, 5, 6.
The sample space for this situation could be written as a list of the possible combinations: H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6.
The sample space for more complicated situations is often shown in a table.
For example,
If flipping the coin and rolling the die were part of a game and the side the coin shows changed the score of the die, you could show this in a sample space diagram. In this game, the coin showing heads adds 1 to the value on the die. The coin showing tails doubles the value on the die.
The sample space diagram shows all the possible outcomes for this game.
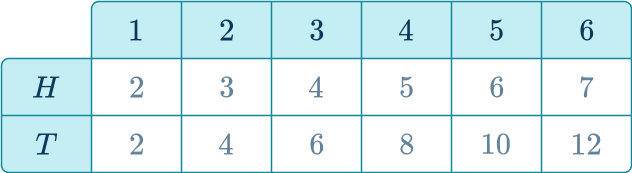
You can use sample space diagrams to find probabilities.
Jon plays the game and wants to know the probability of getting a score of more than 6.
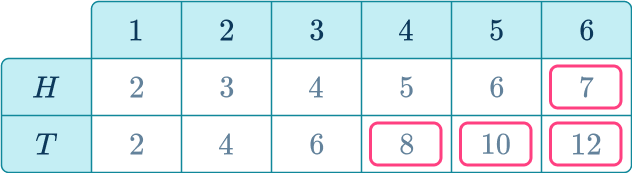
You can see from the table that there are 4 scores more than 6.
There are a total of 12 possible outcomes from this game.
Using the theoretical probability formula,
P( score more than 6) =\cfrac{4}{12}=\cfrac{1}{3}.
What is a sample space?
Common Core State Standards
How does this relate to 7 th grade math?
- Grade 7: Statistics and Probability (7.SP.C.8)
Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation.- a. Understand that, just as with simple events, the probability of a compound event is the fraction of outcomes in the sample space for which the compound event occurs.
- b. Represent sample spaces for compound events using methods such as organized lists, tables and tree diagrams. For an event described in everyday language (example, “rolling double sixes”), identify the outcomes in the sample space which compose the event.
- Design and use a simulation to generate frequencies for compound events. For example, use random digits as a simulation tool to approximate the answer to the question: If 40\% of donors have type A blood, what is the probability that it will take at least 4 donors to find one with type A blood?
![[FREE] Probability Worksheet (Grade 7 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Probability-check-for-understanding-quiz-listing-image.png)
[FREE] Probability Worksheet (Grade 7 to 12)
![[FREE] Probability Worksheet (Grade 7 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Probability-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 7 to 12 students’ understanding of probability. 15+ questions with answers covering a range of 7th to 12th grade probability topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Probability Worksheet (Grade 7 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Probability-check-for-understanding-quiz-listing-image.png)
[FREE] Probability Worksheet (Grade 7 to 12)
![[FREE] Probability Worksheet (Grade 7 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Probability-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 7 to 12 students’ understanding of probability. 15+ questions with answers covering a range of 7th to 12th grade probability topics to identify areas of strength and support!
DOWNLOAD FREEHow to create a sample space
In order to create a sample space:
- Use information provided to decide whether to write a list or create a table to find all possible outcomes.
- Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
Sample space examples
Example 1: sample space of a simple event
A card is drawn from a standard deck of 52 playing cards. Show a sample space for all possible outcomes.
- Use information provided to decide whether to write a list or create a table to find all possible outcomes.

Playing cards have four different suites (clovers or clubs ♣, diamonds ♦, hearts ♥, and spades ♠. Each suite has numbers 2–10 and J, Q, K and A. As there are a large number of cards with some variety, a table can be used to organize the sample space.
2Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
One way to systematically fill in the table is to make each suite a row. Then you can just list the same card numbers/letters for each suite.

Example 2: sample space of a compound event
Show the sample space for all possible outcomes of flipping a coin and spinning the spinner.
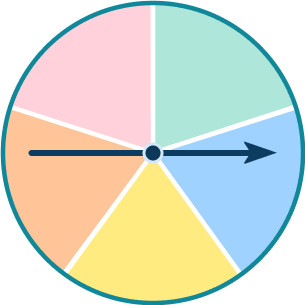
Use information provided to decide whether to write a list or create a table to find all possible outcomes.
A coin has two options: heads or tails. The spinner has 5 options: orange, yellow, blue, green or pink. Using heads (H) and tails (T) as the first outcome, two lists can be made to show all possible outcomes.
Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
When creating a list, it can be helpful to abbreviate the outcomes.
H-O, H-Y, H-B, H-G, H-P
T-O, T-Y, T-B, T-G, T-P
Example 3: sample space of a compound event
Show the sample space for all possible outcomes of rolling a die twice.
Use information provided to decide whether to write a list or create a table to find all possible outcomes.
A standard, 6- sided die has six options: 1, 2, 3, 4, 5, 6. Rolling it twice will create many outcomes, so you can use a table to stay organized.
Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
To systemically fill in the table, make the first row the outcomes for the first roll and the first column the outcome for the second roll. Also list the options 1–6 in order.
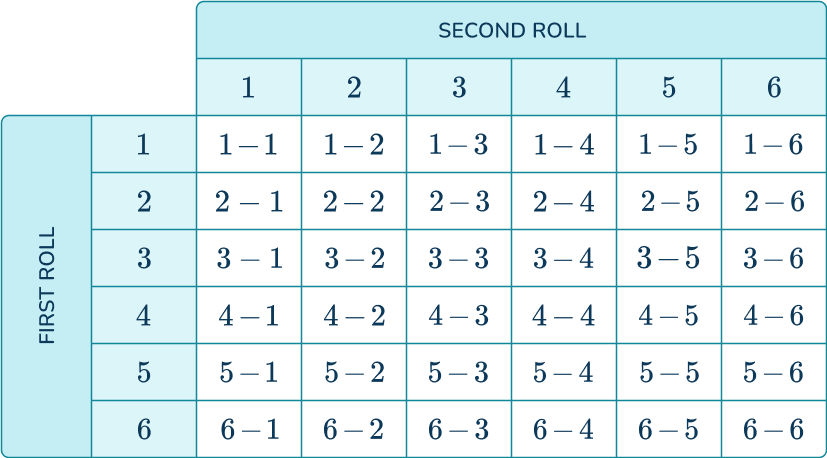
The sample space is all the cells that show the possible outcomes of two rows (outlined in blue). For example, if the first roll is a 2 (right arrow) and the second roll is a 3 (down arrow), the outcome can be found where the two arrows meet.
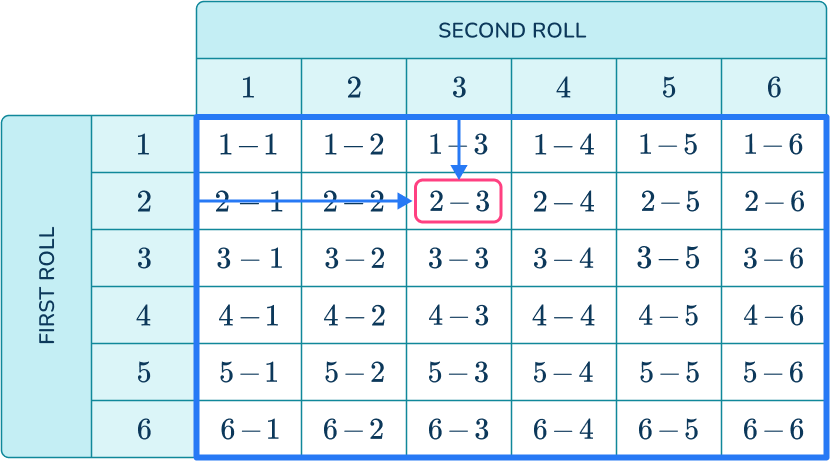
How to use a sample space
In order to find a probability using a sample space diagram:
- Use information provided to decide whether to write a list or create a table to find all possible outcomes.
- Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
- Use the information from the list or table to find any probabilities required.
Example 4: writing a list of possible outcomes
A fair coin is flipped and the spinner is spun.
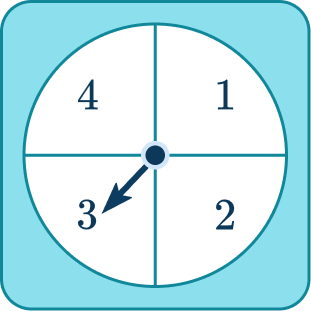
Write a list of all possible combinations of outcomes and find the probability of getting a tail and an even number.
Use information provided to decide whether to write a list or create a table to find all possible outcomes.
The coin has two outcomes: H and T, the spinner has 4 outcomes: 1, 2, 3 and 4. You can write them as pairs, for example, (H, 1).
Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
Start by listing all the head (H) outcomes in order, then the tails (T), to be sure that none get missed.
(H, 1), (H, 2), (H, 3), (H, 4), (T, 1), (T, 2), (T, 3), (T, 4).
Use the information from the list or table to find any probabilities required.
There are two possible outcomes that have a tail (T) and an even number (2 or 4).
(H, 1), (H, 2), (H, 3), (H, 4), (T, 1), {\textbf{(T, 2)}}, (T, 3), {\textbf{(T, 4)}} .
The probability is the ratio of the desired subset (tail and even) over the total possible outcomes.
P( tail and even number ) =\cfrac{2}{8}=\cfrac{1}{4}
Example 5: creating a sample space table
Two fair spinners A and B, one numbered 1, 2 and 3, the other 2, 5, and 7 are spun.
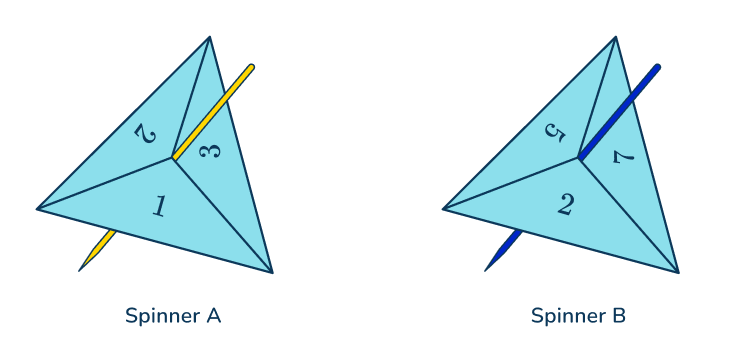
The scores on the spinners are added together. Find the probability that the total score is a prime number.
Use information provided to decide whether to write a list or create a table to find all possible outcomes.
Each spinner has 3 outcomes. You can use a table to show all combinations of the spinners.
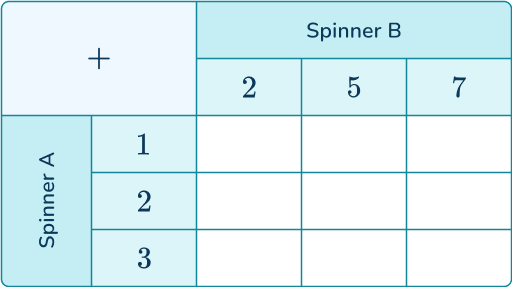
Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
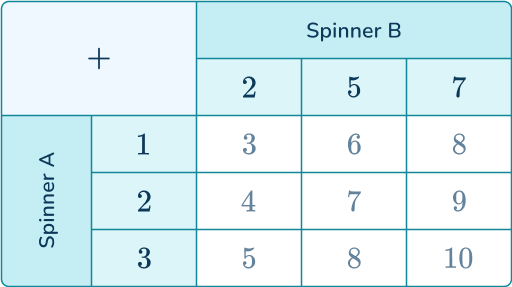
Use the information from the list or table to find any probabilities required.
There are three possible outcomes that are prime.
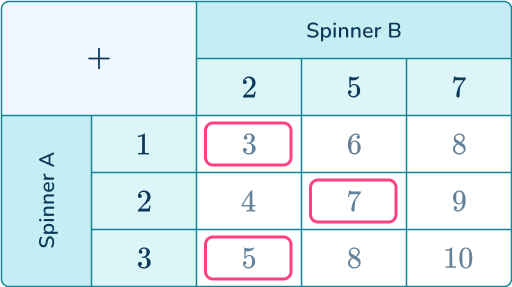
The probability is the ratio of the desired subset (prime) over the total possible outcomes.
P( total score is prime ) =\cfrac{3}{9}
Example 6: creating a sample space diagram using a rule
A fair coin is flipped and a fair six-sided die is rolled. If the coin shows heads, the score on the die is increased by 3. If the coin shows tails the score on the die is decreased by 1. Find the probability of getting a score less than 5.
Use information provided to decide whether to write a list or create a table to find all possible outcomes.
This question is best answered with a table, so you can keep track of the combination of flips/rolls and the total points.
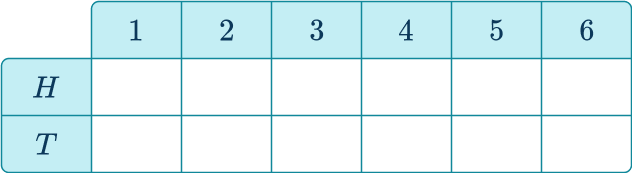
Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
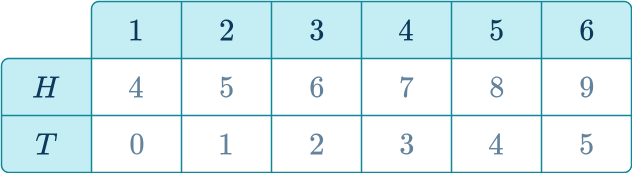
Use the information from the list or table to find any probabilities required.
There are six possible outcomes that are less than 5.
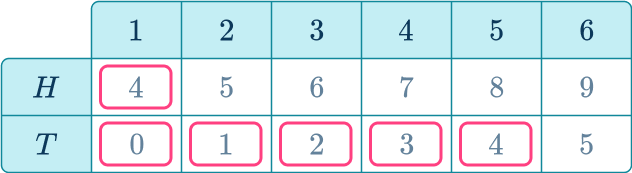
The probability is the ratio of the desired subset ( less than 5) over the total possible outcomes.
P( score less than 5)=\cfrac{6}{12}=\cfrac{1}{2}
Teaching tips for sample space
- Introduce sample space with simple and compound probabilities. Use small, finite sample spaces, such as rolling a die and getting an odd number (simple) or tossing a coin and flipping a coin (compound). Creating sample spaces is the main way that students solve compound probabilities without the rule.
- Help students develop their statistical inference skills by having them estimate the total number of outcomes or the probability of the event before actually creating a sample space. Once they have solved, have them revisit these estimates and discuss how accurate they were and why.
- Once students are comfortable with creating sample spaces, have them complete random experiments to see how the experimental probability compares to the theoretical probability.
Discuss with students why the outcome of the experiment will not always match the calculated probability. This can help them grow ideas about probability space, probability theory and other theorems that will be fostered in more advanced probability topics.
Easy mistakes to make
- Missing out or repeating outcomes when listing
A common error is to miss out some outcomes or repeat one already listed. This leads to the incorrect number of outcomes. It can happen if you do not use a systematic approach to forming the list. Creating a table to list the outcomes can help structure our list to ensure none are missed or repeated.
- Confusing the order of the ratio when calculating the probability of an event
To calculate the probability, write the ratio with the desired outcomes as the numerator and all possible outcomes as the denominator. Confusing this order will lead to the incorrect probability of any event.
Related compound probability lessons
Practice sample space questions
1. Ellie has a bag with 1 green marble, 2 red marbles and 4 blue marbles.
Which choice shows the sample space of randomly picking one marble from Ellie’s bag?
Green, Red, Blue

Green, Red -1, Red -2, Blue -1, Blue -2, Blue -3, Blue -4

Green, Red, Blue, Blue

Green -1, Red -2, Blue -4

If you were to look into Ellie’s bag, this is what you would see.
![]()
The sample space needs to show that there is more than one red and blue marble.
You can number each red and blue to show that there is more than one.

2. A fair coin is flipped and the spinner is spun.
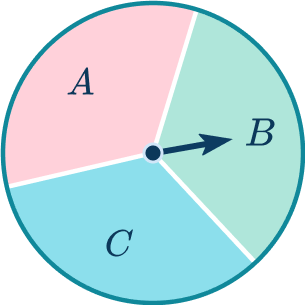
How many possible outcomes are there?




You can create a list showing all possible outcomes. Show the outcomes for heads (H), then tails (T).
H-A, H-B, H-C
T-A, T-B, T-C
3. A fair coin is flipped and the spinner shown below is spun. If the coin shows heads the score on the spinner is doubled. If the coin shows tails the score on the spinner is tripled. Which shows the sample space for this situation?
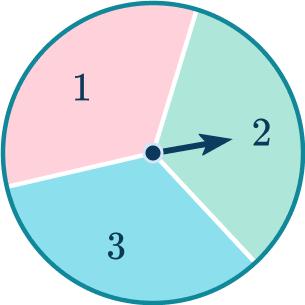
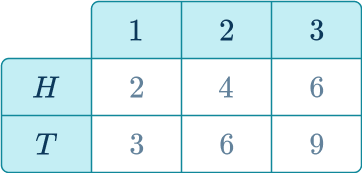

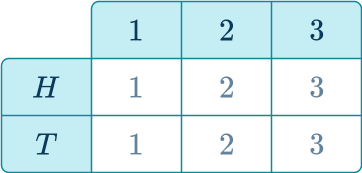

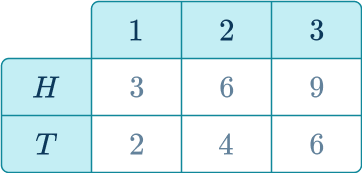

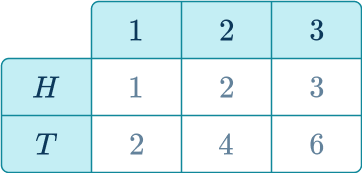

A table works best, since you are applying an operation to each score on the spinner.
The expanded version of the table below, shows how the sample space was calculated.
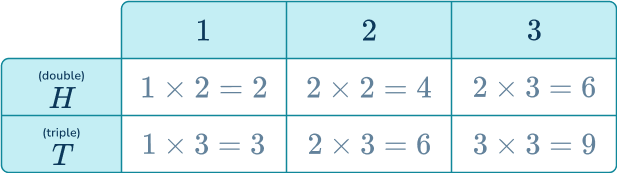
4. The sample space diagram shows the possible outcomes when two normal fair dice are rolled and the difference between values is calculated.
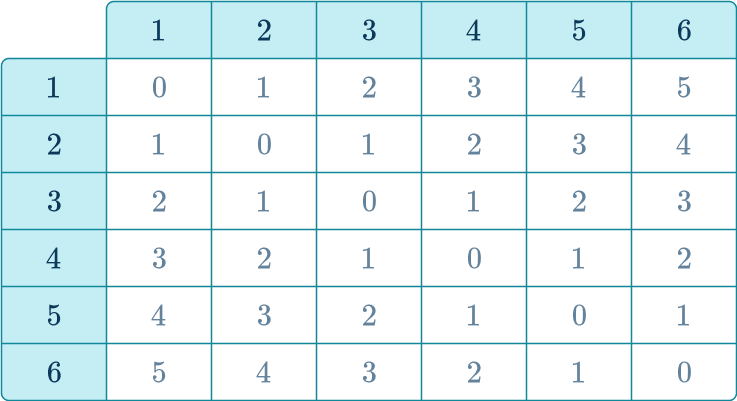
Use the sample space diagram to find the probability of getting a difference of 2 or less.




There are 24 outcomes that are 2 or less out of a total of 36.
\cfrac{24}{36} = \cfrac{2}{3}
5. Three fair coins are flipped together. Each coin has either a head or a tail. Find the probability of getting 2 heads and one tail.




Below is the sample space of three coins flipped:
![]()
There are 3 outcomes which have 2 heads and 1 tail, out of 8 outcomes in total.
6. Two bags each contain 3 numbered counters. Bag A contains the numbers 2, 7 and 9. Bag B contains the numbers 1, 3 and 5.
A counter from each bag is selected at random and their values multiplied together. Find the probability of getting a result greater than 10.




Below is the sample space of choosing a numbered counter from each bag and finding their product:
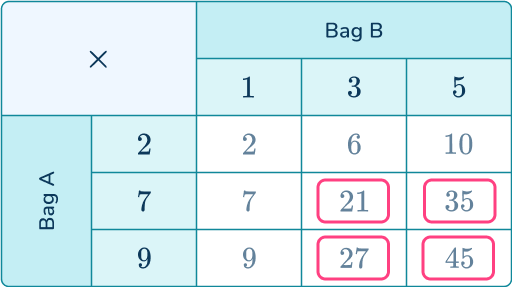
There are 4 outcomes greater than 10, out of 9 outcomes in total.
Sample space FAQs
The intersection of two independent events is when both the events happen together. This can be modeled with a venn diagram or calculated using the rule.
See also: Independent events
The probability of a second event, given that the first event has already occurred.
See also: Conditional probability
The next lessons are
- Probability distribution
- Units of measurement
- Represent and interpret data
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!