Volume of a Triangular Prism - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

3D shapes Area of a triangle Volume formula Parallelograms

Math resources Geometry Volume

Volume of a triangular prism

Here you will learn about the volume of a triangular prism, including how to calculate the volume and how to find a missing length given the volume.

Students will first learn about the volume of a triangular prism as part of geometry in $7$ th grade.

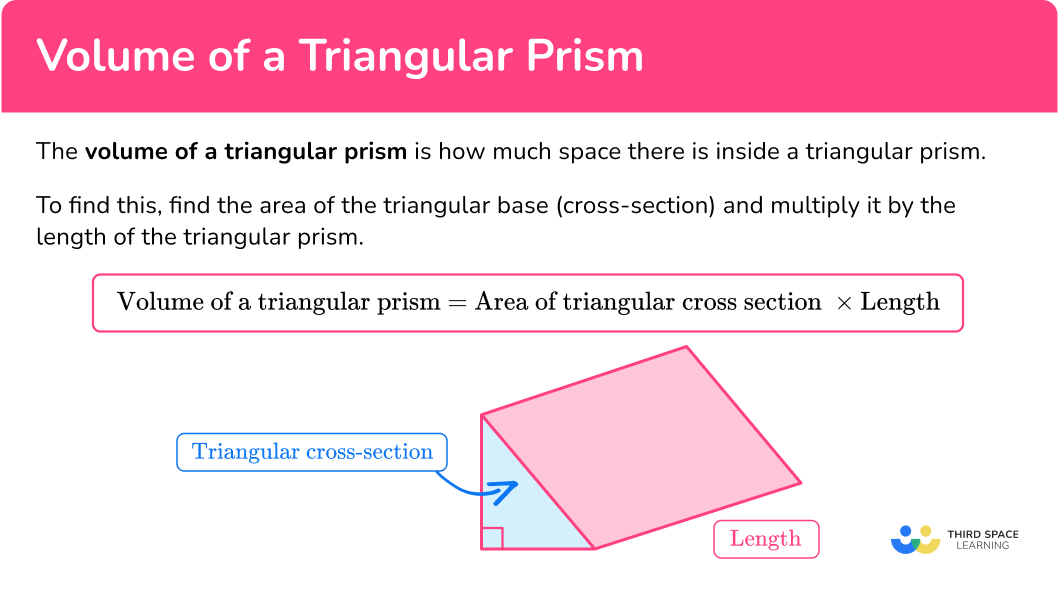
What is the volume of a triangular prism?

The volume of a triangular prism is how much space there is inside a triangular prism. A triangular prism is a polyhedron (3D shape made from polygons) with two congruent triangular ends connected by three rectangles.

To find this, find the area of the triangular base (cross section) and multiply it by the length.

\text{Volume of a triangular prism} = \text{Area of triangular cross section} \times \text{length}

For example,

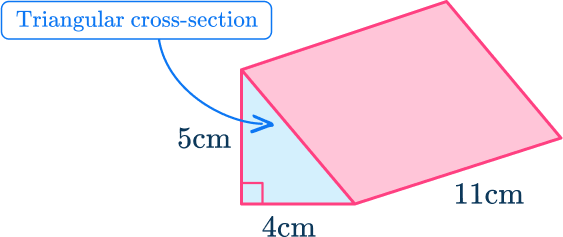
Area of triangular cross-section:

\begin{array}{l}\text{Area }=\cfrac{1}{2}bh \\\\ \text{Area }=\cfrac{1}{2} \times 4 \times 5 \\\\ \text{Area }=10\mathrm{~cm}^{2} \end{array}

Volume of triangular prism:

\, \text{ Volume }= \text{Area of triangular cross-section } \times \text{ length}

\begin{array}{l} \text{Volume }=10 \times 11 \\\\ \text{Volume }=110\mathrm{~cm}^{3}\end{array}

Volume is measured in cubic units (for example, $\mathrm{mm}^3, \mathrm{~cm}^3, \mathrm{~m}^3$ etc).

Calculating a missing length

Sometimes you might be given the volume and some of the measurements of a triangular prism and need to find the other measurements.

This can be done by substituting the values that are known into the volume of a triangular prism formula and solving the equation that is formed.

For example,

The volume of this triangular prism is $105 \mathrm{~cm}^3.$ Find the length, $x,$ of the triangular prism.

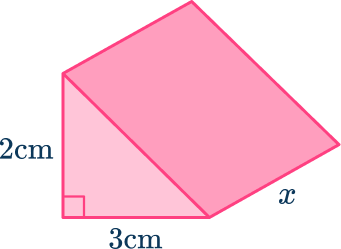
You will still use the following formula,

\text{Volume of a triangular prism} = \text{area of triangular cross section} \times \text{length}

First, calculate the area of the triangular cross-section and substitute everything into the volume of a triangular prism formula, then solve.

\begin{aligned}& \text { Area of triangle }=\cfrac{1}{2} \times b \times h \\\\ & \text { Area of triangle }=\cfrac{1}{2} \times 2 \times 3 \\\\ & \text { Area of triangle }=3\end{aligned}

\text{Volume of a triangular prism} = \text{area of triangular cross section} \times \text{length}

\begin{aligned}& 105=3 \times x \\\\ & 3 x=105 \\\\ & x=35 \end{aligned}

What is the volume of a triangular prism?

Common Core State Standards

How does this relate to $7$ th grade math?

Grade 7: Geometry (7.G.B.6)
Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.

[FREE] Volume Worksheet (Grade 6 to 8)

Use this quiz to check your grade 6 to 8 students’ understanding of volume. 10+ questions with answers covering a range of 6th, 7th and 8th grade volume topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Volume Worksheet (Grade 6 to 8)

DOWNLOAD FREE

How to calculate the volume of a triangular prism

In order to calculate the volume of a triangular prism:

Write down the formula.
Calculate the area of the triangular cross-section and substitute the values.
Solve the equation.
Write the answer, including the units.

Volume of a triangular prism examples

Example 1: volume of a triangular prism

Find the volume of this triangular prism.

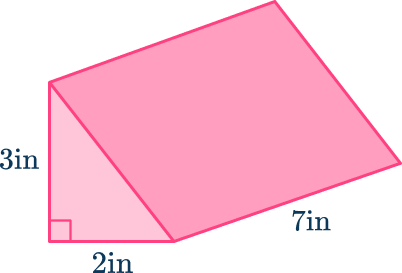
Write down the formula.

\text{Volume of a triangular prism} = \text{Area of triangular cross section} \times \text{length}

2Calculate the area of the triangular cross-section and substitute the values.

The base of the triangle is $2 \mathrm{~in}$ and the height of the triangle is $3 \mathrm{~in}.$

\begin{array}{l}\text{Area of triangle }=\cfrac{1}{2} \times b \times h \\\\ \text{Area of triangle }=\cfrac{1}{2} \times 2 \times 3 \\\\ \text{Area of triangle }=3\end{array}

The area of the triangle is $3 \mathrm{~in}^2.$

The length of the prism is $7 \mathrm{~in}.$

\text{Volume of a triangular prism} = \text{Area of triangular cross section} \times \text{length}

\text{Volume of triangular prism} = 3 \times 7

3Solve the equation.

\begin{aligned}& \text{Volume of triangular prism} =3 \times 7 \\\\ & \text{Volume of triangular prism} = 21 \end{aligned}

4Write the answer, including the units.

The measurements on this triangular prism are in inches, so the volume will be measured in cubic inches.

\text { Volume }=21 \mathrm{~in}^3

Example 2: triangular prism with isosceles triangle

Find the volume of the triangular prism.

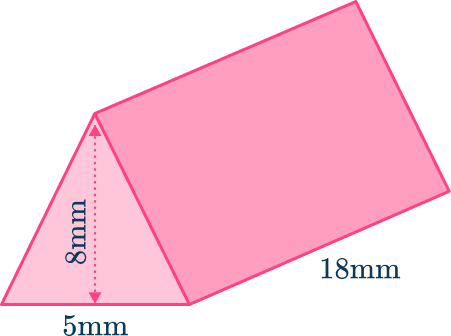
Write down the formula.

\text{Volume of a triangular prism} = \text{Area of triangular cross section} \times \text{length}

Calculate the area of the triangular cross-section and substitute the values.

\begin{array}{l}\text{Area of triangle }=\cfrac{1}{2} \times b \times h \\\\ \text{Area of triangle }=\cfrac{1}{2} \times 5 \times 8 \\\\ \text{Area of triangle }=20 \end{array}

$\text{Volume of a triangular prism} = \text{Area of triangular cross section} \times \text{length}$

$\text{Volume of a triangular prism} = 20 \times 18$

Solve the equation.

\begin{aligned}& \text{Volume of a triangular prism} = 20 \times 18 \\\\ & \text{Volume of a triangular prism} = 360 \end{aligned}

Write the answer, including the units.

The measurements on this triangular prism are in mm, so the volume will be measured in $\mathrm{~mm}^3.$

$\text { Volume }=360 \mathrm{~mm}^3$

Example 3: different units

Find the volume of this triangular prism.

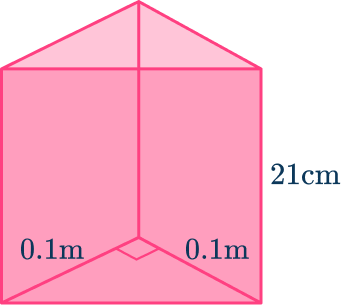
Write down the formula.

\text{Volume of a triangular prism} = \text{Area of triangular cross section} \times \text{length}

Calculate the area of the triangular cross-section and substitute the values.

This time, the triangular prism is the other way up, so start by calculating the area of the base. There are some measurements in both m and cm here, so you will need to make the units the same before you begin solving. The easiest thing to do in this example is to convert $0.1 \mathrm{~m}$ to $10 \mathrm{~cm}.$

\begin{array}{l}\text{Area of triangle }=\cfrac{1}{2} \times b \times h \\\\ \text{Area of triangle }=\cfrac{1}{2} \times 10 \times 10 \\\\ \text{Area of triangle }=50\end{array}

Since the triangular prism is the other way up, the length that we need to multiply by is the height of the prism, $21 \mathrm{~cm}.$

\text{Volume of a triangular prism }= \text{ Area of triangular cross-section }\times { length}

$\text{Volume of a triangular prism } = 50 \times 21$

Solve the equation.

\begin{aligned}& \text{Volume of triangular prism} = 50 \times 21 \\\\ & \text{Volume of triangular prism} = 1050 \end{aligned}

Write the answer, including the units.

The measurements that are used for this triangular prism are in cm, so the volume will be measured in $\mathrm{~cm}^3.$

$\text { Volume }=1050 \mathrm{~cm}^3$

How to find a missing length given the volume

Write down the formula.
Calculate the area of the triangular cross-section and substitute everything into the volume of a triangular prism formula.
Solve the equation.
Write the answer, including the units.

Missing length examples

Example 4: finding a missing length

The volume of this triangular prism is $168 \mathrm{~cm}^3.$ Find the length, $x,$ of the triangular prism.

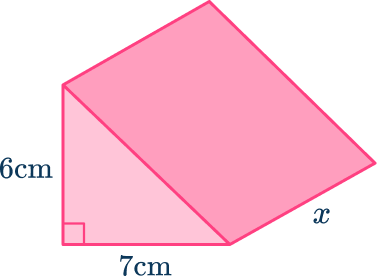
Write down the formula.

\text{Volume of a triangular prism} = \text{area of triangular cross section} \times \text{length}

Calculate the area of the triangular cross-section and substitute everything into the volume of a triangular prism formula.

\begin{array}{l}\text{Area of triangle }=\cfrac{1}{2} \times b \times h \\\\ \text{Area of triangle }=\cfrac{1}{2} \times 7 \times 6 \\\\ \text{Area of triangle }=21\end{array}

\text{Volume of a triangular prism } = \text{ area of triangular cross-section } \times { length}

$168=21 \times x$

Solve the equation.

\begin{aligned}& 21x=168 \\\\ & x=8\end{aligned}

Write the answer, including the units.

x=8 \mathrm{~cm}

Example 5: finding a missing height

The volume of this triangular prism is $80 \mathrm{~mm}^3.$ Find the height of the prism.

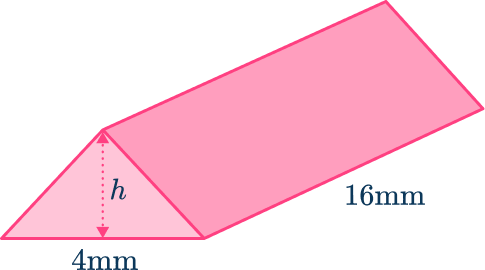
Write down the formula.

\text{Volume of a triangular prism} = \text{area of triangular cross section} \times \text{length}

Calculate the area of the triangular cross-section and substitute everything into the volume of a triangular prism formula.

\begin{array}{l}\text{Area of triangle }=\cfrac{1}{2} \times b \times h \\\\ \text{Area of triangle }=\cfrac{1}{2} \times 4 \times h \\\\ \text{Area of triangle }=2h \\\\ \end{array}

\text{Volume of a triangular prism }=\text{ area of triangular cross-section } \times { length}

\begin{aligned} &80=2h \times 16 \\\\ &80=32h\end{aligned}

Solve the equation.

\begin{aligned}&32h=80 \\\\ &h=2.5\end{aligned}

Write the answer, including the units.

h=2.5 \mathrm{~mm}

Example 6: finding a missing base, different units

The volume of this triangular prism is $440 \mathrm{~mm}^2.$ Find the length labeled $y.$

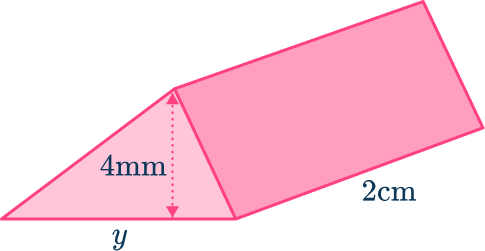
Write down the formula.

\text{Volume of a triangular prism} = \text{area of triangular cross section} \times \text{length}

Calculate the area of the triangular cross-section and substitute everything into the volume of a triangular prism formula.

\begin{array}{l}\text{Area of triangle }=\cfrac{1}{2} \times b \times h \\\\ \text{Area of triangle }=\cfrac{1}{2} \times y \times 4 \\\\ \text{Area of triangle }=2y\end{array}

Notice here that you need to work in mm since the volume is in $mm^{3}.$ Therefore you need to convert $2 \mathrm{~cm}$ to $20 \mathrm{~mm}.$

\text{Volume of a triangular prism } = \text{ area of triangular cross-section } \times { length}

\begin{aligned} &440=2y \times 20 \\\\ &440=40y \end{aligned}

Solve the equation.

\begin{aligned}& 40y=440 \\\\ & y=11\end{aligned}

Write the answer, including the units.

y=11 \mathrm{~mm}

Teaching tips for volume of a triangular prism

Find different representations to use during instruction to appeal to all the different learning styles in your classroom. This includes diagrams, equations and verbal cues.

Find technology tools to incorporate in teaching, including interactive whiteboards and interactive manipulatives.

Make sure that triangular prism volume worksheets have a variety of problem types to challenge students and reinforce understanding.

Easy mistakes to make

Missing units or using incorrect units
You should always include units in your answer.
Volume is measured in units cubed ( $\mathrm{mm}^3, \mathrm{~cm}^3, \mathrm{~m}^3$ etc).

Calculating with different units
You need to make sure all measurements are in the same units before calculating volume. Example, you can’t have some in cm and some in $m.$

Using the wrong formula
Be careful to apply the correct prism related formula to the correct question type.

Practice volume of a triangular prism questions

110 \mathrm{~cm}^{3}

55 \mathrm{~cm}^{3}

240 \mathrm{~cm}^{3}

120 \mathrm{~cm}^{3}

\begin{aligned} \text{Area of triangle }&=\cfrac{1}{2} \times 3 \times 8 \\\\ &=12\mathrm{~cm}^{2}\end{aligned}

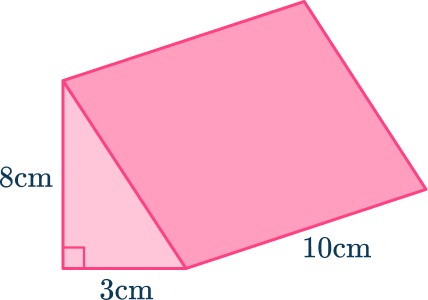
\begin{aligned}\text{Volume of triangular prism }&=12 \times 10 \\\\ &=120\mathrm{~cm}^{3}\end{aligned}

252 \mathrm{~cm}^{3}

42 \mathrm{~cm}^{3}

1764 \mathrm{~cm}^{3}

126 \mathrm{~cm}^{3}

\begin{aligned}\text{Area of triangle }&=\cfrac{1}{2} \times 6 \times 6 \\\\ &=18\mathrm{~cm}^{2}\end{aligned}

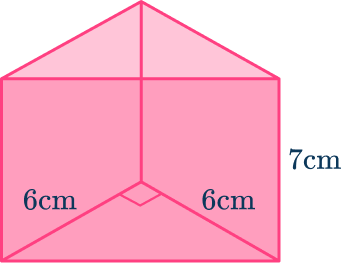
\begin{aligned}\text{Volume of triangular prism }&=18 \times 7 \\\\ &=126\mathrm{~cm}^{3}\end{aligned}

924 \mathrm{~mm}^{3}

9.24 \mathrm{~cm}^{3}

92.4 \mathrm{~mm}^{3}

9240 \mathrm{~mm}^{3}

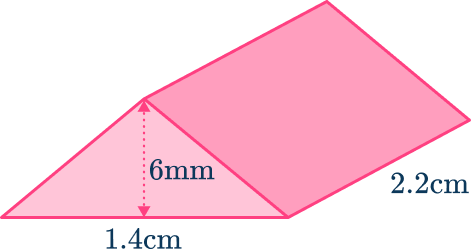
Notice that one of the measurements is in $mm$ and the others are in $cm.$ Change $1.4 \mathrm{~cm}$ to $14 \mathrm{~mm}$ and $2.2 \mathrm{~cm}$ to $22 \mathrm{~mm}.$

\begin{aligned}\text{Area of triangle}&=\cfrac{1}{2} \times 14 \times 6 \\\\ &=42\mathrm{~mm}^{2}\end{aligned}

\begin{aligned}\text{Volume of triangular prism }&=42 \times 22 \\\\ &=924\mathrm{~mm}^{3}\end{aligned}

3.5\mathrm{~cm}

2,016\mathrm{~cm}

7\mathrm{~cm}

1,008\mathrm{~cm}

\begin{aligned}\text{Area of triangle }&=\cfrac{1}{2} \times 3 \times 8 \\\\ &=12\mathrm{~cm}^{2}\end{aligned}

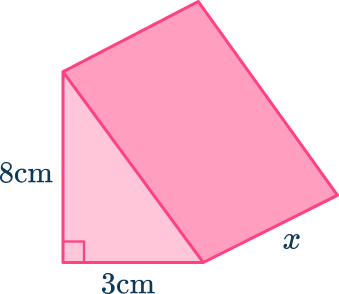
\begin{aligned}\text{Volume of triangular prism }&=12 \times x \\\\ 84&= 12x \\\\ 7&=x\end{aligned}

The length is $7 \mathrm{~cm}.$

45 \mathrm{~m}

9 \mathrm{~m}

2.5 \mathrm{~m}

4.5 \mathrm{~m}

\begin{aligned}\text{Area of triangle }&=\cfrac{1}{2} \times 6 \times h \\\\ &=3h\end{aligned}

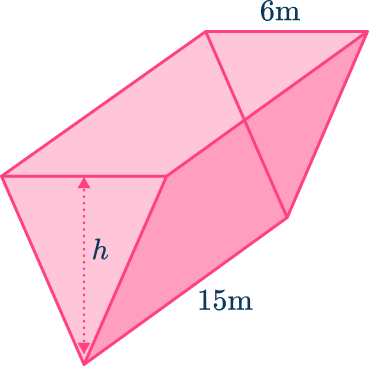
\begin{aligned}\text{Volume of triangular prism }&=3h \times 15\\\\405 &= 45h \\\\ 9&=h\end{aligned}

The height is $9 \mathrm{~m}.$

5 \mathrm{~cm}

0.25 \mathrm{~cm}

0.5 \mathrm{~cm}

4,050 \mathrm{~cm}

\begin{aligned}\text{Area of triangle }&=\cfrac{1}{2} \times 4 \times y \\\\ &=2y\end{aligned}

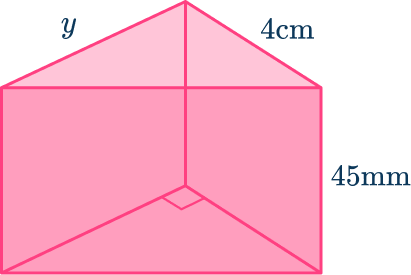
Notice that the height of the triangular prism is in $mm$ , however the volume is in $cm^3.$ Therefore, you need to change $45 \mathrm{~mm}$ to $4.5 \mathrm{~cm}.$

\begin{aligned}\text{Volume of triangular prism }&=2y \times 4.5\\\\ 45&= 9h \\\\ 5&=h\end{aligned}

The length of $y$ is $5 \mathrm{~cm}.$

Volume of a triangular prism FAQs

What is the difference between a triangular prism and a rectangular prism?

A triangular prism is a 3D shape with triangular bases and rectangular faces or sides with $9$ vertices. A rectangular prism is a 3D shape with $6$ rectangular sides or faces that meet at right angles with $8$ vertices.

Can the triangular base of the prism have different sizes?

In a triangular prism, the bases must be identical triangles, which ensures that the prism has a uniform cross-section throughout its length.

What is Heron’s formula?

Heron’s formula is a formula used to find the area of a triangle in terms of the length of its sides. It can be applied to any type of triangle, including equilateral triangles.

Heron’s formula is $A=\sqrt{s(s-a)(s-b)(s-c)}$

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.