A sphere is a set of points in space that are equidistant distance [katex] (r) [/katex] from the center. It is commonly known as a [katex] 3 [/katex]D solid shape that has no sides or vertices.

Volume of a Sphere - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Polygons 3D shapes Sphere shape Volume formula

Math resources Geometry Volume

Volume of a sphere

Here you will learn about the volume of a sphere, including how to calculate the volume of a sphere given its radius and how to find the volume of a hemi-sphere.

Students will first learn about the volume of a sphere as a part of geometry in $8$ th grade and will expand on their understanding in high school.

What is the volume of a sphere?

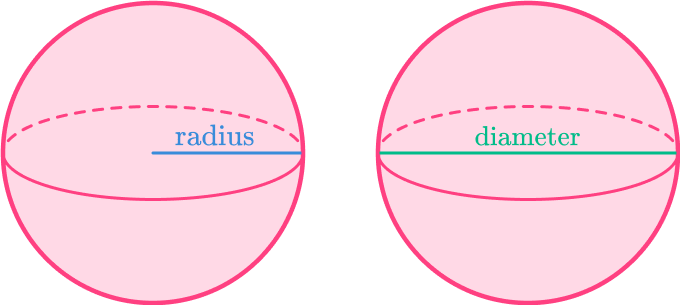
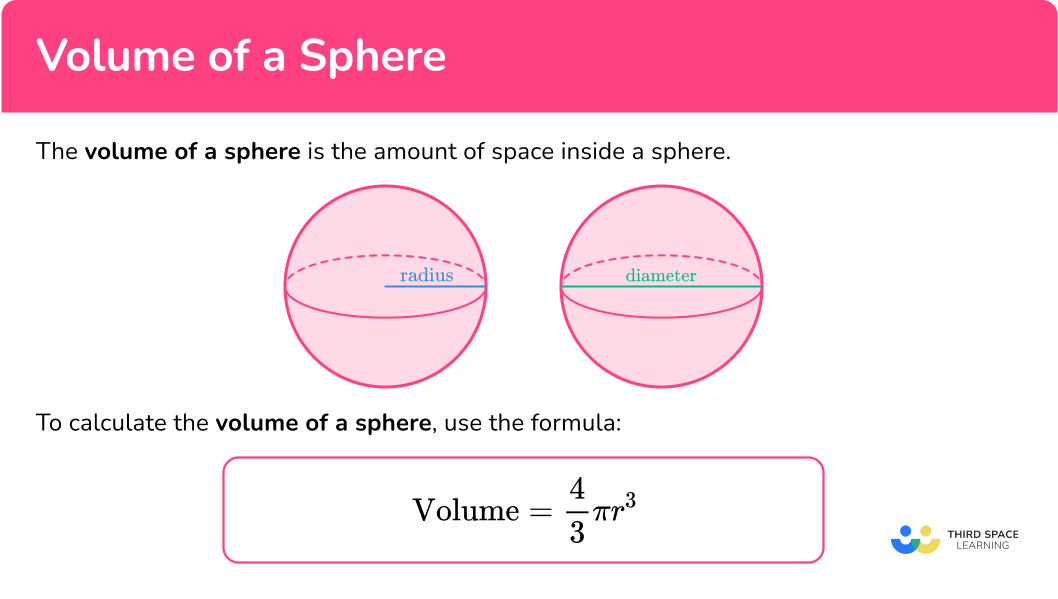
The volume of a sphere is the amount of space inside a sphere. A sphere is a three-dimensional shape that is perfectly round, with no edges or vertices.

The radius of a sphere is the fixed distance from the center of the sphere to any given point on its surface. The diameter of the sphere is a straight line that passes through the center and connects two points on the sphere.

To calculate the volume of a sphere, use the formula:

$V=\cfrac{4}{3} \; \pi r^3$

Notice the cube of the radius $\mathrm(r^3)$ in the volume formula. Volume is a measure in three-dimensions so the units for the volume are cubic units. For example, cubic feet $\mathrm(ft^3),$ cubic inches $\mathrm(in^3)$ and cubic centimeters $\mathrm(cm^3).$

For example,

Find the volume of the sphere with a radius of $5~{cm}.$

$\begin{aligned} \text{Volume}&=\frac{4}{3} \pi r^3 \\\\ &= \frac{4}{3} \times \pi \times 5^3\\\\ &=\frac{500}{3}\pi\\\\ &=523.6 \ cm^3 \ \text{(to 1 dp)}\\\\ \end{aligned}$

The answer should be stated in cubic centimeters because the units used are centimeters.

[FREE] Volume Worksheet (Grade 6 to 8)

Use this quiz to check your grade 6 to 8 students’ understanding of volume. 10+ questions with answers covering a range of 6th, 7th and 8th grade volume topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Volume Worksheet (Grade 6 to 8)

DOWNLOAD FREE

Calculating the radius given the volume

In order to calculate the radius of a sphere given the volume, you need to rearrange the formula for the volume of a sphere $(V=\cfrac{4}{3} \; \pi r^3)$ to make $r$ (the radius) the subject of the formula.

For example,

Now you have the formula for determining the radius of a sphere given the volume as:

$r=\sqrt[3]{\cfrac{3V}{4\pi}}$

What is the volume of a sphere?

Common Core State Standards

How does this relate to $8$ th grade and high school math?

Grade 8: Geometry (8.G.C.9)
Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.

High school: Geometry (HS.G.GMD.A.3)
Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.

How to calculate the volume of a sphere

In order to calculate the volume of a sphere:

Write down the formula for the volume of a sphere.
Substitute given values into the formula.
Complete the calculation.
Write the answer, including the units.

Volume of a sphere examples

Example 1: volume of a sphere given the radius

Calculate the volume of a sphere with radius $6~{cm}.$ Write your answer to $1$ decimal place.

Write down the formula for the volume of a sphere.

The formula for the volume of a sphere is $V=\cfrac{4}{3} \; \pi r^3.$

2Substitute given values into the formula.

Substitute the value of the radius $r=6$ into the formula.

V=\cfrac{4}{3} \times \pi \times 6^3

3Complete the calculation.

Use a calculator to find the volume.

V=288 \pi =904.7786842…

4Write the answer, including the units.

Here you are asked to give the answer to $1$ decimal place.

The volume of the sphere is: $904.8 \mathrm{~cm}^3 \; (1dp).$

Example 2: decimal radius

Find the volume of a sphere with radius $7.2~{cm}.$ Write your answer to $2$ decimal places.

Write down the formula for the volume of a sphere.

V=\cfrac{4}{3} \; \pi r^3

Substitute given values into the formula.

Substituting the value $r=7.2~{cm}$ into the formula for the volume of a sphere, you have:

$V=\cfrac{4}{3} \times \pi \times 7.2^3$

Complete the calculation.

Use a calculator to find the volume.

$V=1563.457566\dots$

Write the answer, including the units.

Here you are asked to write the answer to $2$ decimal places.

$V=1563.46$ $(2$ dp $)$

The volume of the sphere is: $1563.46 \mathrm{~cm}^3 \; (2dp).$

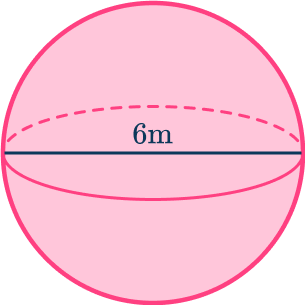
Example 3: volume of a sphere given the diameter – in terms of pi (π)

Calculate the volume of a sphere with a diameter of $6~{m}.$ Write your answer in terms of $\pi.$

Write down the formula for the volume of a sphere.

V=\cfrac{4}{3} \; \pi r^3

Substitute given values into the formula.

The radius is half the length of the diameter and so,

$r=6\div{2}=3\text{m}.$

Substitute the value of the radius into the formula.

$V=\cfrac{4}{3} \times \pi \times 3^3$

Complete the calculation.

V=36\pi

Write the answer, including the units.

Here you are asked to write the answer in terms of pi $(\pi).$

$V= 36\pi \; m^3$

The volume of the sphere is $36\pi \text{ m}^3$ .

Example 4: volume of a hemisphere

Find the volume of a hemisphere with radius $8~{cm}.$ Write your answer to $1$ decimal place.

Write down the formula for the volume of a sphere.

A hemisphere has half the volume of a sphere, so you will divide the volume of a sphere by $2\text{:}$

$V=(\cfrac{4}{3} \; \pi r^3) \div{2}$

Substitute given values into the formula.

Given that $r=8,$ you have:

$V=(\cfrac{4}{3} \times \pi \times 8^3)\div{2}$

Complete the calculation.

Use a calculator to work out the volume.

$V=\cfrac{1024}{3} \; \pi$

Write the answer, including the units.

Here you are asked to write the answer to $1$ decimal place.

$V=\cfrac{1024}{3}\pi = 1072.330292… = 1072.3 \; cm^3 \ (1dp)$

The volume of the hemisphere is $1072.3 \mathrm{~cm}^3$ .

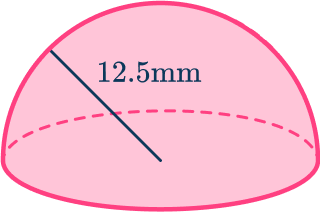
Example 5: volume of a hemisphere

Find the volume of a hemisphere with radius $12.5 \mathrm{~mm}.$

Give your answer to $2$ decimal places.

Write down the formula for the volume of a sphere.

Remember, a hemisphere has half the volume of the equivalent sphere.

$V=\cfrac{4}{3} \; \pi r^3 \div{2}$

Substitute given values into the formula.

Substitute the value of the radius into the formula.

$V=\cfrac{4}{3} \times \pi \times 12.5^3\div{2}$

Complete the calculation.

Use a calculator to find the volume.

$V=4090.615434\dots$

Write the answer, including the units.

Here you are asked to give the answer to $2$ decimal places.

$V=4090.615434 \ldots=4090.62 \mathrm{~mm}^3 \; (2dp)$

The volume of the hemisphere is $4090.62 \mathrm{~mm}^3 \; (2dp).$

How to calculate the radius of a sphere given the volume

In order to calculate the radius of the sphere given the volume:

Write down the formula for the radius of a sphere, in terms of the volume.
Substitute the given values into the formula.
Complete the calculation.
Write the answer, including the units.

Calculating the radius of a sphere examples

Example 6: calculating the radius given the volume

The total volume of a sphere is $3,000 \mathrm{~cm}^3.$ Calculate the radius of the sphere, correct to $2$ decimal places.

Write down the formula for the radius of a sphere, in terms of the volume.

r=\sqrt[3]{\cfrac{3V}{4\pi}}

Substitute the given values into the formula.

You are given the volume, so substitute this into the formula to calculate the radius:

$r=\sqrt[3]{\cfrac{3\times{3000}}{4\pi}}$

Complete the calculation.

\begin{aligned} & r=\sqrt[3]{\frac{9000}{4 \pi}} \\\\ & =\sqrt[3]{716.1972439 \ldots} \\\\ & =8.947002289 \ldots \end{aligned}

Write the answer, including the units.

Here you are asked to give the answer to $2$ decimal places.

$r=8.947002289 \ldots=8.95 \mathrm{~cm} \; (2dp)$

The radius of the sphere is $8.95 \mathrm{~cm} \;(2dp).$

Example 7: calculating the radius given the volume

Calculate the radius of a sphere with the volume $8,460 m^3.$ Write your answer to the nearest centimeter.

Write down the formula for the radius of a sphere, in terms of the volume.

Use the formula,

$r=\sqrt[3]{\cfrac{3V}{4\pi}}$

Substitute the given values into the formula.

Substituting the value for the volume, you have

$r=\sqrt[3]{\cfrac{3\times{8460}}{4\pi}}$

Complete the calculation.

\begin{aligned} & r=\sqrt[3]{\cfrac{25380}{4 \pi}} \\\\ & =\sqrt[3]{2019.676228 \ldots} \\\\ & =12.64039323 \ldots \end{aligned}

Write the answer, including the units.

Here you are asked to give the answer to the nearest centimeter.

$r=12.64039323 \ldots=12.64 \mathrm{~m}=1264 \mathrm{~cm}$

The radius of the sphere is $1264 \mathrm{~cm}.$

Teaching tips for volume of a sphere

Make sure to use visual representations, such as diagrams and physical spheres, to allow students to recognize the shape and structure of spheres.

Work through examples, giving students step-by-step instructions on how to find the volume of the sphere. Displaying it within the classroom will give students a place to refer back to when needed.

While worksheets with practice questions have a place within the classroom, allow students to use interactive tools and engage in conversations with other students about different types of problems.

Easy mistakes to make

Using the incorrect formula
Students are learning several formulas during middle school and high school geometry that can be used. It’s important that students have a general basis of each formula, so they know which to use in each mathematical situation.

Rounding too soon during the calculation
It is important to not round the answer until the end of the calculation. This will mean your final answer is accurate. It is useful to keep your answer in terms of \pi until you round the answer at the very end of the question.

Using the wrong units
For area, use square units such as $\mathrm{cm}^2.$ For volume, use cube units such as $\mathrm{cm}^3.$ An easy way for students to remember this is that you find the area of $2$ D shapes and volume of $3$ D shapes.

Mixing up the radius and the diameter
It is a common error to mix up radius and diameter. Remember the radius is half of the diameter, and the diameter stretches across the entire sphere.

Practice volume of a sphere questions

4188.8 \mathrm{~cm}^3

314.2 \mathrm{~cm}^3

1.3 \mathrm{~cm}^3

1256.6 \mathrm{~cm}^3

You are finding the volume of a sphere so substitute the value of $r$ into the formula.

\begin{aligned} V&=\cfrac{4}{3} \pi r^3 \\\\ &= \cfrac{4}{3} \times \pi \times 10^3\\\\ &=\cfrac{4000}{3}\pi\\\\ &=4188.790205… \\\\ &=4188.8 \ cm^3 \ \text{(1dp)}\\\\ \end{aligned}

10,536.7 \mathrm{~cm}^3

2,324.3 \mathrm{~cm}^3

1,317.1 \mathrm{~cm}^3

581.1 \mathrm{~cm}^3

The radius is half the value of the diameter, and so,

r=13.6 \div 2=6.8 \mathrm{~cm}

Substituting $r=6.8$ into $V=\cfrac{4}{3} \pi r^3,$ we have

\begin{aligned} V&=\cfrac{4}{3} \pi r^3 \\\\ &= \cfrac{4}{3} \times \pi \times 6.8^3\\\\ &=1317.089682… \\\\ &=1317.1 \; \text{cm}^3\text{ (1dp)} \end{aligned}

243\pi \mathrm{~cm^3}

108\pi \mathrm{~cm^3}

972\pi \mathrm{~cm^3}

729\pi \mathrm{~cm^3}

Substituting $r=9$ into the formula for the volume of a sphere, you have:

\begin{aligned} V&=\cfrac{4}{3} \pi r^3 \\\\ &= \cfrac{4}{3} \times \pi \times 9^3\\\\ &=972\pi \\\\ \end{aligned}

33,510 \mathrm{~mm}^3

16,755 \mathrm{~mm}^3

1,257 \mathrm{~mm}^3

3,770 \mathrm{~mm}^3

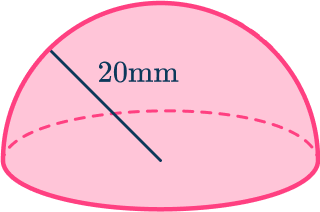
When finding the volume of a hemisphere, calculate half of the volume of a sphere.

\begin{aligned} V&=(\cfrac{4}{3} \pi r^3) \div{2}\\\\ &= (\cfrac{4}{3} \times \pi \times 20^3) \div{2}\\\\ &=\cfrac{16 000}{3} \pi\\\\ &=16 755.16082… \\\\ &=16 755{~mm}^3 (0dp) \end{aligned}

2304 \pi \mathrm{~km^3}

7240 \mathrm{~km^3}

1152\pi \mathrm{~km^3}

3620 \mathrm{~km^3}

When finding the volume of a hemisphere, calculate half of the volume of a sphere.

\begin{aligned} V&=\cfrac{4}{3} \pi r^3 \div{2}\\\\ &= \cfrac{4}{3} \times \pi \times 12^3 \div{2}\\\\ &=1152\pi \\\\ &=1152\pi \ km^3\\\\ \end{aligned}

7.1 \mathrm{~cm}

18.9 \mathrm{~cm}

37.8 \mathrm{~cm}

11.3 \mathrm{~cm}

Using the formula for the radius in terms of the volume, substitute the value of the volume and solve to find the radius.

\begin{aligned} & r=\sqrt[3]{\cfrac{3 V}{4 \pi}} \\\\ & =\sqrt[3]{\cfrac{3 \times 1500}{4 \pi}}\\\\ & =\sqrt[3]{358.098622 \ldots} \\\\ & =7.101240423 \ldots \\\\ & =7.1 \mathrm{~cm} \; (1 \mathrm{dp}) \end{aligned}

Volume of a sphere FAQs

What is a sphere?

A sphere is a set of points in space that are equidistant distance $(r)$ from the center. It is commonly known as a $3$ D solid shape that has no sides or vertices.

What is the formula for the volume of a sphere?

The formula for the volume of a sphere is $V=\cfrac{4}{3} \pi r^3,$ where $r$ is the radius of the sphere.

How do you find the surface area of a sphere?

To find the surface area of a sphere, you will use the formula $A=4 \pi r^2,$ where $r$ is the radius and $\pi$ is the mathematical constant.

What is the Archimedes’ principle?

The Archimedes’ principle is a fundamental principle of physics, discovered by the ancient Greek mathematician, Archimedes, that states when a body is partially or fully submerged in a fluid, it experiences an upward buoyant force that is equal to the weight of the fluid displaced by the body.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.