Sphere Shape - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

2D shapes Polygons

Math resources Geometry 3D shapes

Sphere shape

Here you will learn about the sphere shape, including how to identify a sphere shape based on its properties, how to identify a sphere shape within a composite shape, and how to find the volume and surface area of a sphere shape.

Students will first learn about spheres as part of geometry in $1$ st grade. They will expand their learning in middle school and high school when they learn how to find the volume and surface area of a sphere shape.

What is a sphere shape?

The sphere shape is a three-dimensional shape with a curved surface. Unlike other 3D shapes, such as a cube, cuboid, cone, or cylinder, a sphere has no faces (no flat surfaces), no edges, and no vertex. Every point of its surface is an equal distance away from the center of the sphere.

A hemisphere is half of a sphere. It has one circular base, which is a flat face, and one edge. Like a sphere, it has no vertices.

Properties of a sphere shape

The sphere is a three-dimensional shape with a curved surface. Unlike other 3D shapes, such as a cube, cuboid, cone, or cylinder, a sphere has no faces (no flat surfaces), no edges, and no vertex.

Real life examples of a sphere shape

There are many real life examples of spherical objects.

For example,

Note: The following content does not apply until middle school or high school.

Volume of a sphere shape

The volume of a sphere is the amount of space there is inside a sphere. The volume of a sphere is measured in cubic units.

The formula for the volume of a sphere is:

$\text{Volume}=\cfrac{4}{3} \, \pi{r}^3$

For example, find the volume of the sphere.

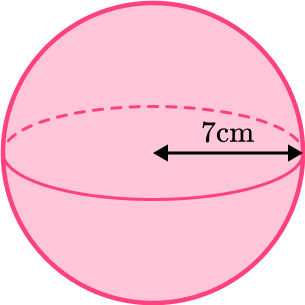
This radius of the sphere is $7 {~cm}$ .

$\begin{aligned} \text{Volume}&=\cfrac{4}{3} \, \pi r^3 \\\\ &= \cfrac{4}{3} \times \pi \times 7^3\\\\ &=\cfrac{1372}{3} \, \pi\\\\ &=1436.755… \\\\ &=1440 \ cm^3 \ \text{(3sf)}\ \end{aligned}$

See also: Volume of a sphere

Surface area of a sphere shape

The surface area of a sphere is the area which covers the outer surface of a sphere.

The surface area of a sphere is measured in square units.

The formula for the surface area of a sphere is:

$\text{Surface Area}=4 \, \pi r^2$

For example, find the surface area of the sphere.

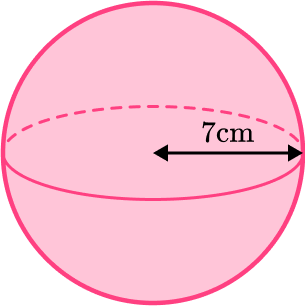
This radius of the sphere is $7 \, cm.$

$\begin{aligned} \text{Surface area}&=4 \, \pi r^2\\\\ &=4 \times \pi \times 7^2\\\\ &=196 \, \pi\\\\ &=615.752…\\\\ &=616 \ cm^2 \ \text{(to 3 sf)}\ \end{aligned}$

See also: Surface area of a sphere

What is a sphere shape?

Common Core State Standards

How does this relate to $1$ st grade math?

Grade 1 – Geometry (1.G.2)
Compose two-dimensional shapes (rectangles, squares, trapezoids, triangles, half-circles, and quarter-circles) or three-dimensional shapes (cubes, right rectangular prisms, right circular cones, and right circular cylinders) to create a composite shape, and compose new shapes from the composite shape.

How to identify a sphere shape

In order to determine if a shape is a sphere:

Look at the shape and examine its properties.
Determine if it has the properties of a sphere.

3a If it does, name the shape as a sphere.

3b If it does not, describe the difference in properties.

[FREE] 3D Shape Check for Understanding (Grade 1, 5 and 6)

Use this quiz to check your grade 1, 5 and 6 students’ understanding of 3D shape. 10+ questions with answers covering a range of 1st, 5th and 6th grade 3D shape topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] 3D Shape Check for Understanding (Grade 1, 5 and 6)

DOWNLOAD FREE

Sphere shape examples

Example 1: identify a sphere

Is this shape a sphere?

Look at the shape and examine its properties.

The shape has a curved surface, one flat face, and one edge. It has no vertices.

2Determine if it has the properties of a sphere.

A sphere has a curved surface, no faces, no edges, and no vertices. This shape has some properties in common with a sphere, but there are some differences.

3If it does not, describe the difference in properties.

The shape shown has one flat face and one edge, while a sphere has no faces or edges. The shape shown is a hemisphere which is half of a sphere.

Example 2: identify a sphere

Is this object a sphere?

Look at the shape and examine its properties.

The object has a curved surface, no flat faces, no edges, and no vertices.

Determine if it has the properties of a sphere.

A sphere has a curved surface, no flat faces, no edges, and no vertices. It has all of the properties of a sphere.

If it does, name the shape as a sphere.

This object is a sphere.

How to identify a sphere in a composite shape

In order to identify spheres within composite shapes:

Look at all the shapes within the composite shape and examine their properties.
Determine if any of the shapes have the properties of a sphere. If they do, identify them.
Answer the question about the composite shape.

Example 3: identify a sphere in a composite shape

There is one sphere in this composite shape. What color is it?

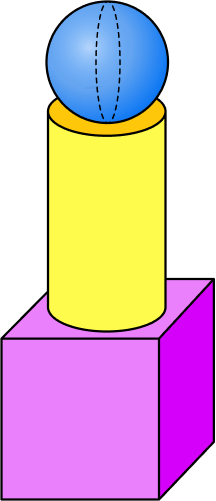
Look at all the shapes within the composite shape and examine their properties.

There are three shapes within the composite shape. The purple shape is rectangular and has $6$ faces, $12$ edges, and $8$ vertices.

The yellow shape has $2$ circular faces, no vertices, $2$ edges, and a curved surface. The blue shape has a curved surface, no flat faces, no edges, and no vertices.

Determine if any of the shapes have the properties of a sphere. If they do, identify them.

The blue shape on top has the same properties of a sphere.

Answer the question about the composite shape.

The sphere is blue.

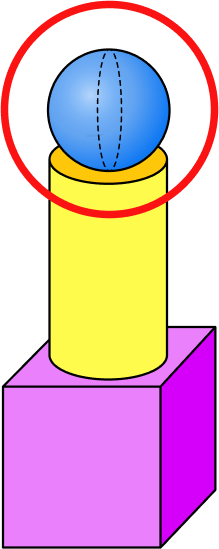
Example 4: identify a sphere in a composite shape

How many spheres are in this composite shape?

Look at all the shapes within the composite shape and examine their properties.

There are $8$ shapes in this composite shape.

Red and purple shapes (bottom): These shapes are rectangular; they each have $6$ faces, $12$ edges, and $8$ vertices.

Blue and green shapes (middle): These shapes each have $2$ circular faces, no vertices, $2$ edges, and a curved surface.

Red, orange and blue shapes (on top): These shapes have a curved surface, no flat faces, no edges, and no vertices.

Determine if any of the shapes have the properties of a sphere. If they do, identify them.

The red, orange, and blue shapes on top of the composite shape have the properties of a sphere.

Answer the question about the composite shape.

There are $3$ spheres in this composite shape.

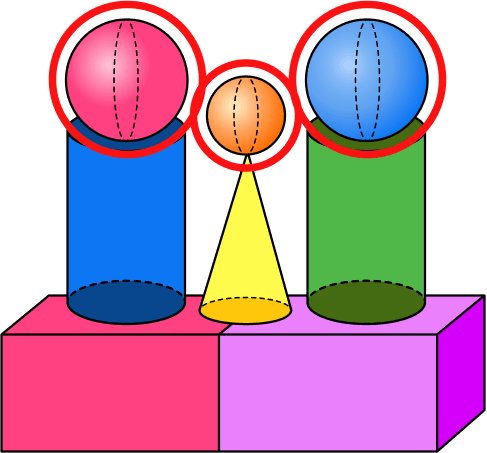
How to calculate the volume or surface area of a sphere

In order to calculate the volume of a sphere or the surface area of a sphere:

Write down the formula.
Substitute the given values.
Work out the calculation.
Write the final answer.

Middle school sphere shape examples

Example 5: volume of a sphere

Calculate the volume of a sphere of radius $12 {~}cm$ . Give your answer to the nearest whole number.

Write down the formula for the volume of a sphere.

$\text{Volume} =\cfrac{4}{3} \, \pi r^3$

Substitute the given values into the formula.

$V=\cfrac{4}{3} \times \pi \times 12^3$

Complete the calculation.

$\begin{aligned}&=2304 \, \pi \\\\ &=7238.229…\\\end{aligned}$

Write the final answer, including the units.

Volume is measured in cubic units. The radius is given in centimeters, so the volume will be in cubic centimeters.

The volume of the sphere is $7240 {~cm^3}$ (to the nearest whole number).

Example 6: surface area of a sphere given the diameter – in terms of π

Find the surface area of a sphere with the diameter of $20 {~m}.$ Leave your answer in terms of $\pi.$

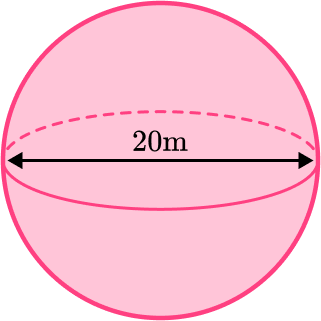
Write down the formula for the surface area of a sphere.

$\text{Surface Area }=4 \, \pi{r}^{2}$

Substitute the given values into the formula.

The diameter of the sphere is $20 {~m}$ and so we need to use this to calculate the radius and the surface area of the sphere.

$20\div2=10$

The radius of the sphere is $10 {~m}$ .

We now know the radius of the sphere is $10 {~m},$ so we substitute $r=10$ into the formula for the surface area.

$SA=4\times\pi\times{10}^{2}$

Complete the calculation.

$SA=400 \, \pi$

Write the final answer, including the units.

Surface area is measured in square units. The radius is measured in meters so the surface area is measured in square meters $(m^2)$ , with the solution in terms of $\pi$ .

The surface area of the sphere is $400 \, \pi {m^2}$ .

Teaching tips for sphere shape

Begin by introducing the concept of a sphere as a three-dimensional shape that is round and ball-shaped. Use simple language and emphasize that spheres are completely symmetrical.

Utilize visual aids such as pictures, diagrams, or real-life objects to help students visualize what a sphere looks like. Show them examples of spheres such as balls, balloons, fruits like oranges, or even Earth globes to reinforce the concept.

Compare spheres with other shapes like circles and cubes. Point out the differences and similarities between the shape of a sphere and other 2D and 3D shapes. Highlight that circles are flat two-dimensional shapes, while spheres are three-dimensional shapes with a curved surface.

Easy mistakes to make

Thinking that all circles are spheres
Children may confuse spheres with circles. They might think that any object with a circular shape, such as a coin or a drawing of a circle, is a sphere. It is important to explain that a circle is a two-dimensional shape (2D shape), while a sphere is a three-dimensional object (3D shape).

Thinking that spheres are flat on the bottom
Children may have difficulty understanding that a sphere is a completely symmetrical shape, meaning it doesn’t have a flat surface on the bottom. They might imagine a sphere as having a flat base like other solid shapes or objects they are familiar with, such as a cup or a plate.

Labeling volume or surface area of a sphere in the incorrect units
Volume is measured in cubic units such as ${cm^3}, {m^3}, {ft^3}.$
Surface area is measured in square units such as ${cm^2}, {m^2}, {ft^2}.$

Hemisphere shape
Cone
Triangular pyramid
Pyramid shape
Square pyramid
3D shape names
Cylinder
Angles of elevation and depression

Practice sphere shape questions

Sphere Shape image 14 US

Sphere Shape image 15 US

Sphere Shape image 16 US

Sphere Shape image 17 US

A sphere has a curved surface, no flat faces, no edges, and no vertices. Every point of its surface is an equal distance away from the center of the sphere.

The last shape has all of these properties and the others do not.

Sphere Shape image 18 US

Sphere Shape image 20 US

Sphere Shape image 19 US

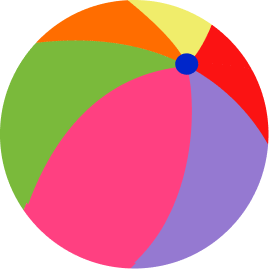
Sphere Shape image 20 US-1

A sphere has a curved surface, no flat faces, no edges, and no vertices. Every point of its surface is an equal distance away from the center of the sphere.

All shapes except the second shape, which is a hemisphere, have these properties.

2

1

3

4

A sphere has a curved surface, no flat faces, no edges, and no vertices. Every point of its surface is an equal distance away from the center of the sphere.

The red shape on the top and the orange shape have all of these properties.

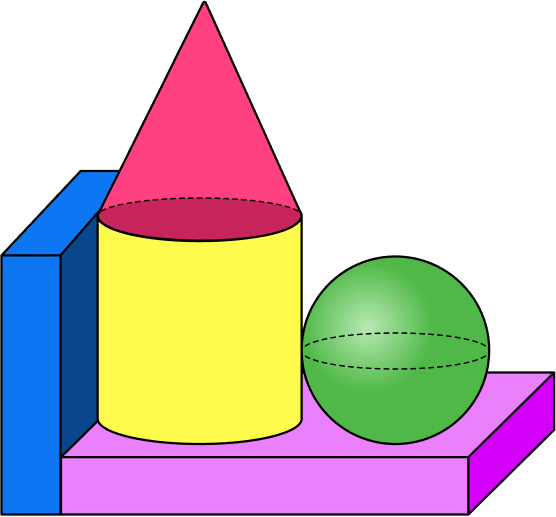
red

green

yellow

blue

A sphere has a curved surface, no flat faces, no edges, and no vertices. Every point of its surface is an equal distance away from the center of the sphere.

The green shape has all of these properties.

Middle school practice sphere shape questions

333.04 \mathrm{~cm}^3

330 \mathrm{~m}^3

58.09 \mathrm{~cm}^3

232.35 \mathrm{~cm}^3

We are finding the volume of a sphere, so we substitute the value of the radius $r=4.3$ into the formula $V=\cfrac{4}{3} \, \pi{r}^{3}.$

$\begin{aligned}\text{Volume}&=\cfrac{4}{3} \, \pi r^3 \\\\ &= \cfrac{4}{3} \times \pi \times 4.3^3\\\\ &=333.0381428… \\\\ &=333.04\text{~cm}^{3} \ \text{(to the nearest hundredth)}\end{aligned}$

270\text{ cm}^2

407.72\text{ cm}^2

66.48\text{ cm}^2

265.90\text{ cm}^2

We are finding the surface area of a sphere, so we substitute the value of the radius $r=4.6$ into the formula $SA=4 \, \pi {r^2}$ .

$\begin{aligned}\text{Surface area}&=4 \, \pi r^2\\\\ &=4 \times \pi \times 4.6^2\\\\ &=265.9044022…\\\\ &=265.90 \text{~cm}^2 \ \text{(2dp)}\\\end{aligned}$

Sphere shape FAQs

What is a sphere?

A sphere is a three-dimensional shape that is perfectly round and ball-shaped. It has a curved surface that is the same distance from its center at all points.

What are the properties of a sphere?

A sphere has a curved surface, no flat faces, no edges, and no vertices. Every point of its surface is an equal distance away from the center of the sphere.

What are some examples of spheres?

Some examples of spheres are balls (like a basketball or soccer ball), oranges, marbles, globes, and soap bubbles.

What is a spheroid?

A spheroid is a three-dimensional shape that is similar to a sphere but not perfectly round.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.