1) Which shape is an example of a cone?

2) Which shape is an example of a cone?

Cone - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

2D shapes Quadrilaterals Area Angles

Math resources Geometry 3D shapes

Cone

Here you will learn about cones, including how to classify and identify a cone, how to find the volume of a cone and how to find the surface area of a cone.

Students will first learn about a cone as part of geometry in $1$ st grade. They will expand their learning in middle school and high school when they learn how to find the volume and surface area of a cone.

What is a cone?

A cone is a three dimensional object that tapers from a circular base to a point. The term cone comes from the Greek word, “konos”, meaning a wedge or peak.

There is more than one type of cone, and the cone most commonly used is referred to as a “right circular cone”.

Examples of cones:

Right circular cone	Oblique cone

Real-life examples of cone like shapes include traffic cones, ice cream cones, volcano shapes, and party hats.

Parts of a cone:

Base

The base of the cone is a circle.

Vertex or apex

The vertex or apex of the cone is the point where all lateral sides meet.

Dimensions of a cone

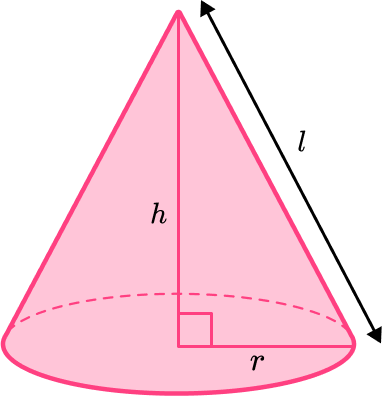
The radius of the base of a cone is $r$ .

The perpendicular height of a cone is $h$ . The height of the cone is a line segment that connects the apex to the center of the circular base. It is perpendicular to the base of the cone.

The slant height of a cone is $l$ . The slant height of the cone is the distance from any point on the base to the apex, along the curved surface of the cone.

Volume of a cone

The volume of a cone is how much space there is inside a cone.

The formula for the volume of a cone is:

$\text{Volume}=\cfrac{1}{3} \, \pi r^2 h$

For example, find the volume of the cone, rounded to the nearest tenth.

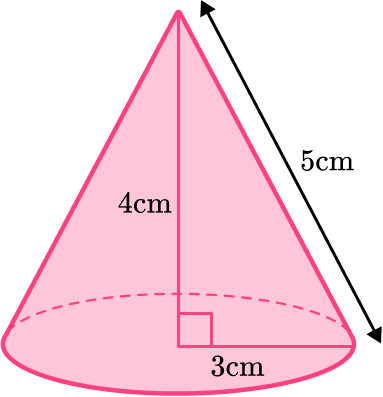
$\begin{aligned} \text { Volume of cone }&=\cfrac{1}{3} \, \pi r^2 h \\\\ & =\cfrac{1}{3} \times \pi \times 3^2 \times 4 \\\\ & =12 \pi \\\\ & =37.7 \mathrm{~cm}^3 \end{aligned}$

Surface area of a cone

The surface area of a cone is the area which covers the outer surface of a cone.

The surface area is made up of two parts, a curved surface area and a circular base.

The formula for calculating the curved surface area of a cone is:

$\text{Curved surface area}=\pi rl$

The formula for calculating the area of a circle:

$\text{Area of circle}=\pi r^2$

For the TOTAL surface area, you can add the two parts together:

$\text{TOTAL surface area}=\pi rl+\pi r^2$

For example, find the surface area rounded to the nearest tenth.

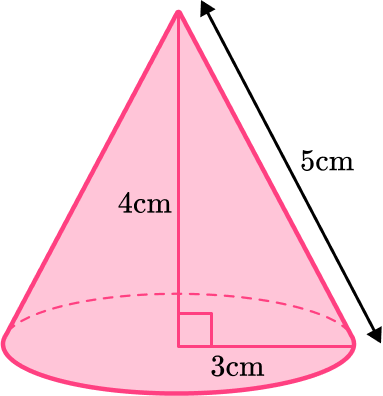
$\text{Curved surface area}=\pi rl=\pi \times 3\times 5=15\pi$

$\text{Area of circle}=\pi r^2=\pi \times 3^2=9\pi$

$\text{TOTAL surface area}= 15\pi + 9\pi = 24\pi = 75.4 {~cm}^2$

What is a cone?

Common Core State Standards

How does this relate to $1$ st, $7$ th and $8$ th grade math?

Grade 1: Geometry (1.G.A.2)
Compose two-dimensional shapes (rectangles, squares, trapezoids, triangles, half-circles, and quarter-circles) or three-dimensional shapes (cubes, right rectangular prisms, right circular cones, and right circular cylinders) to create a composite shape, and compose new shapes from the composite shape.

Grade 7: Geometry (7.G.B.6)
Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.

Grade 8: Geometry (8.G.C.9)
Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.

How to identify a cone

In order to identify a cone, you will:

Look for the characteristics of a cone.
State whether or not the shape is a cone.
If the shape is not a cone, explain what characteristics are different.

[FREE] 3D Shape Check for Understanding (Grade 1, 5 and 6)

Use this quiz to check your grade 1, 5 and 6 students’ understanding of 3D shape. 10+ questions with answers covering a range of 1st, 5th and 6th grade 3D shape topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] 3D Shape Check for Understanding (Grade 1, 5 and 6)

DOWNLOAD FREE

Cone examples

Example 1: cone example

Look at the image below and determine if it is a cone or not.

Look for the characteristics of a cone.

A cone has a circular base with a curved surface area that meets at a vertex that is directly above the center of the circular base.

This shape also has a circular base and a curved surface area that meets at a vertex.

2State whether or not the shape is a cone.

This shape is a cone because it has a circular base with a curved surface that meets at a vertex.

Example 2: cone example

Look at the image below and determine if it is a cone or not.

Look for the characteristics of a cone.

A cone has a circular base with a curved surface area that meets at a vertex that is directly above the center of the circular base.

This shape has a rectangular base with $4$ triangular faces that meet at a vertex.

State whether or not the shape is a cone.

This shape is a pyramid, not a cone.

If the shape is not a cone, explain what characteristics are different.

This shape has a rectangular base with $4$ triangular faces that meet at a vertex.

How to calculate the volume of a cone

In order to calculate the volume of a cone:

Write down the formula.
Substitute the given values.
Calculate the volume of the cone.
Write the final answer, including the units.

Volume of a cone examples

Example 3: volume of a cone

Find the volume of the cone with radius $5.3{~cm}$ and perpendicular height $7.8{~cm}$ .

Give your answer to the nearest centimeter.

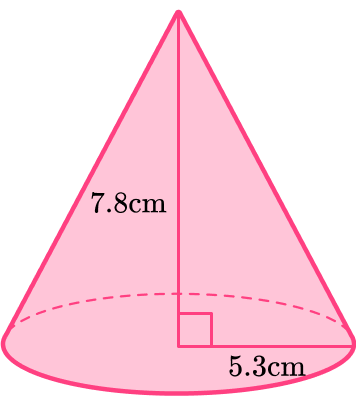
Write down the formula.

$\text {Volume }=\cfrac{1}{3} \, \pi r^{2} h$

Substitute the given values.

$\begin{aligned} & r=5.3 \\\\ & h=7.8 \end{aligned}$

$\begin{aligned} \text { Volume } &=\cfrac{1}{3} \, \pi r^{2} h \\\\ &=\cfrac{1}{3} \times \pi \times 5.3^{2} \times 7.8 \end{aligned}$

Calculate the volume of the cone.

$\begin{aligned} &=\cfrac{1}{3} \times \, \pi \times 5.3^{2} \times 7.8 \\\\ &=229.443 \ldots \end{aligned}$

Write the final answer, including the units.

The answer rounded to the nearest centimeter is $V = 229 {~cm}^3$ .

Example 4: volume of a cone

Find the volume of the cone with radius $9{~cm}$ and perpendicular height $11{~cm}$ .

Leave your answer in terms of $\pi$ .

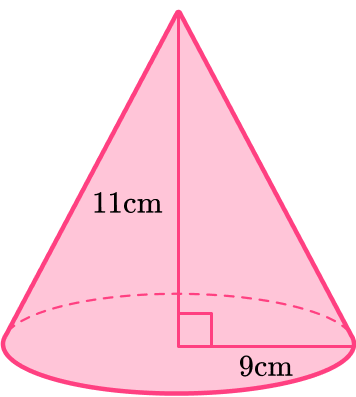
Write down the formula.

$\text {Volume }=\cfrac{1}{3} \, \pi r^{2} h$

Substitute the given values.

$\begin{aligned} & r=9 \\\\ & h=11 \end{aligned}$

$\begin{aligned} \text { Volume } &=\cfrac{1}{3} \, \pi r^{2} h \\\\ &=\cfrac{1}{3} \times \pi \times 9^{2} \times 11 \end{aligned}$

Calculate the volume of the cone.

$\begin{aligned} &=\cfrac{1}{3} \times \, \pi \times 9^{2} \times 11 \\\\ &=297 \pi \end{aligned}$

Write the final answer, including the units.

The question asks for the answer in terms of $\pi$ so the final answer is

$=297 \pi {~cm}^3$

How to calculate the surface area of a cone

In order to calculate the surface area of a cone:

Calculate the area of each face.
Add the area of each face together.
Include the units.

Surface area of a cone examples

Example 5: total surface area of a cone

Find the curved surface area of the cone with radius $4.3{~cm}$ and slant height $9.6{~cm}$ .

Give your answer to the nearest centimeter.

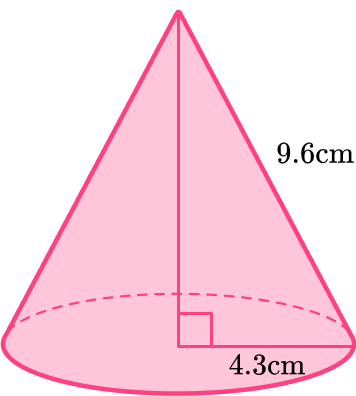
Calculate the area of each face.

$\begin{aligned} \text {Curved surface area} &= \, \pi r l \\\\ &=\pi \times 4.3 \times 9.6 \\\\ &=129.6849 \ldots \\\\ &=129.7 \text { (round to the nearest tenth) } \end{aligned}$

$\begin{aligned} \text {Area of circle } &= \, \pi r^2 \\\\ &=\pi \times 4.3^2 \\\\ &=58.0880 \ldots \\\\ &=58.1 \text { (rounded to the nearest tenth) } \end{aligned}$

Add the area of each face together.

Total surface area: $129.7+58.1=187.8$

Include units.

Surface area $=188 \; cm^2$

Example 6: total surface area of a cone

Find the curved surface area (lateral area) of the cone with radius $8{~cm}$ and slant height $13{~cm}$ .

Leave your answer in terms of $\pi$ .

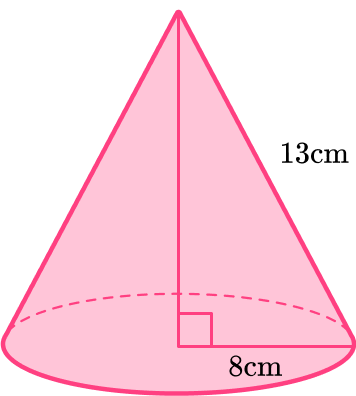
Calculate the area of each face.

$\begin{aligned} \text{Curved surface area}&=\, \pi rl\\\\ &=\pi \times 8 \times 13\\\\ &= 104 \pi \end{aligned}$

$\begin{aligned} \text{Area of circle }&=\, \pi r^2\\\\ &=\pi \times 8^2\\\\ &=64\pi \end{aligned}$

Add the area of each face together.

Total surface area: $104\pi +64\pi = 168\pi$

Include units.

$=168 \pi \mathrm{~cm}^{2}$

Teaching tips for cone

Introduce and reinforce important vocabulary words, such as base, vertex, height, slant height, lateral surface area, and volume. Make sure to encourage students to use these terms correctly when discussing cones.

Provide hands-on activities for students to explore and manipulate cone shapes. For example, you can give them playdough or clay to create their own cones, or ask them to cut out and fold paper cones.

Allow students to practice calculating the volume and surface area of cones. You can also give them worksheets or problem-solving tasks involving cone calculations to reinforce their understanding.

Easy mistakes to make

Incorrectly applying a formula
There are several formulas that can be used, so you would need to match the correct formula to the correct context.
For example, it would be easy to mix up $\pi r^2 + \pi r$ , the formula to find the area of a circle, and the formula to find the volume of a cone,
$\text {Volume }=\cfrac{1}{3} \, \pi r^2 h.$

Confusing the radius and diameter
It is a common error to mix up radius and diameter. Remember, the radius of the cone is half of the distance across the circular base, and the diameter is the full distance across the circular base.
For example,

Use of incorrect units
It’s easy for students to mix up when to use the different types of units. For area, you use square units such as ${~cm}^2$ , and for volume, you use cubic units such as ${~cm}^3$ .

Hemisphere shape
Sphere shape
Triangular pyramid
Pyramid shape
Square pyramid
3D shape names
Cylinder
Angles of elevation and depression

Practice cone questions

Cone image 18 US

Cone image 19 US

Cone image 20 US

Cone image 21 US

This shape has a circular base with a curved surface area that meets at a vertex that is directly above the center of the circular base.

Cone image 22 US

This shape is a cone.

Cone image 23 US

Cone image 24 US

Cone image 25 US

Cone image 26 US

This shape has a circular base with a curved surface area that meets at a vertex that is directly above the center of the circular base.

Cone image 22 US

This shape is a cone.

805 {~cm}^3

806 {~cm}^3

745 {~cm}^3

746 {~cm}^3

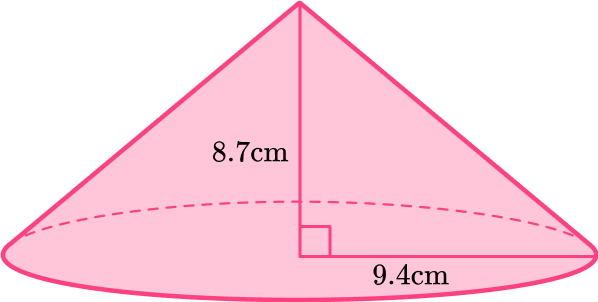
Find the volume of a cone so you can substitute the values of $r$ and $h$ into the formula.

$\begin{aligned} & r=9.4 \\\\ & h=8.7 \end{aligned}$

$\begin{aligned} & V=\cfrac{1}{3} \, \pi r^2 h \\\\ & V=\cfrac{1}{3} \times \pi \times 9.4^2 \times 8.7 \end{aligned}$

$V=805.014 \ldots$

( $805.014$ rounded to the nearest whole number would give you…)

$V=805 \mathrm{~cm}^3$

127 \pi {~cm}^3

126 \pi {~cm}^3

128 \pi {~cm}^3

125 \pi {~cm}^3

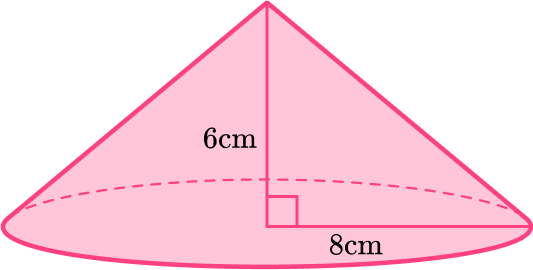
Find the volume of a cone so you can substitute the values of $r$ and $h$ into the formula.

$\begin{aligned} & r=8 \\\\ & h=6 \\\\ & V=\cfrac{1}{3} \, \pi r^2 h \\\\ & V=\cfrac{1}{3} \times \pi \times 8^2 \times 6 \\\\ & V=128 \pi \\\\ & V=128 \pi \mathrm{~cm}^3 \end{aligned}$

83.7 {~cm}^2

360.1 {~cm}^2

360.2 {~cm}^2

83.8 {~cm}^2

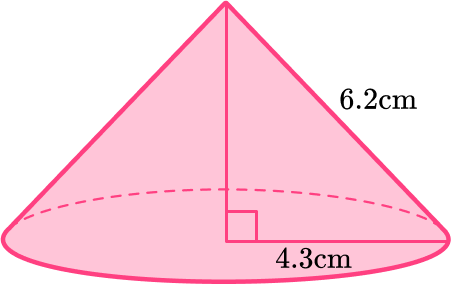
You will find the curved surface area of a cone, so you can substitute the values of $r$ and $h$ into the formula.

$\begin{aligned} \text{Curved surface area}&= \, \pi r l \\\\ & =\pi \times 4.3 \times 6.2 \\\\ & =83.754 \ldots \text{ (round to the nearest tenth)}\\\\ & =83.8 \mathrm{~cm}^2 \end{aligned}$

61 \pi{~cm}^2

63 \pi{~cm}^2

62 \pi{~cm}^2

64 \pi{~cm}^2

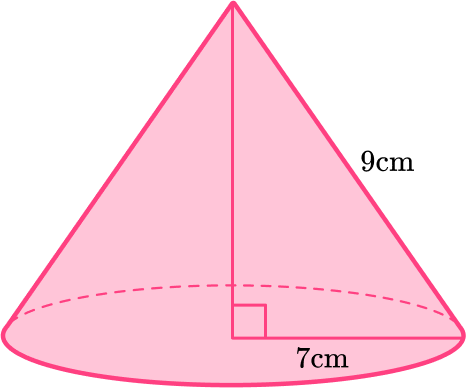
You are finding the curved surface area of a cone, so substitute the values of $r$ and $l$ into the formula.

$\begin{aligned} \text{Curved surface area}&= \,\pi rl\\\\ &=\pi \times 7\times 9\\\\ &=63\pi\\\\ &=63\pi \ cm^2\\\\ \end{aligned}$

Cone FAQs

What is the difference between a right circular cone and an oblique cone?

A right circular cone is the most common type of cone. It has a circular base, and the apex is directly above the center of the base. The axis of the cone is perpendicular to the base, creating a right angle. An oblique cone is any cone that is not a right circular cone. In an oblique cone, the axis is not perpendicular to the base, resulting in a slanted shape.

What are the different types of cones?

During your math journey, you will encounter right circular cones, oblique cones, acute cones, and obtuse cones.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.