Pyramid Shape - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

2D shapes Quadrilaterals Area Angles

Math resources Geometry 3D shapes

Pyramid shape

Here you will learn about the pyramid shape, including what a pyramid is, how to calculate the volume of a pyramid and how to calculate the surface area of a pyramid.

Students will first learn about pyramids as part of geometry in $1$ st grade. They will expand their learning in middle school and high school when they learn how to find the volume and surface area of a pyramid shape.

What is the pyramid shape?

A pyramid is a three dimensional geometric shape (3D shape) made up of flat faces: a base and triangular faces which meet at a point called the apex.

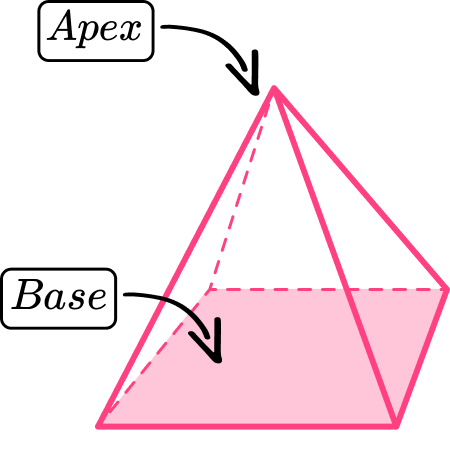
Three main features of pyramids are, faces, vertices and edges:

Face – a closed, flat surface.
Edge – connects two faces.
Vertex (pl. vertices) – a point where three or more edges meet.

[FREE] Pyramid Shape Worksheet (Grade 1 to 8)

Use this worksheet to check your grade 1 to 8 students’ understanding of pyramid shapes. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Pyramid Shape Worksheet (Grade 1 to 8)

Use this worksheet to check your grade 1 to 8 students’ understanding of pyramid shapes. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

You can label the vertices (corners) of a pyramid to identify certain edges or faces. Below is an example of a triangular pyramid where the letters $A$ – $D$ represent the $4$ vertices of the pyramid.

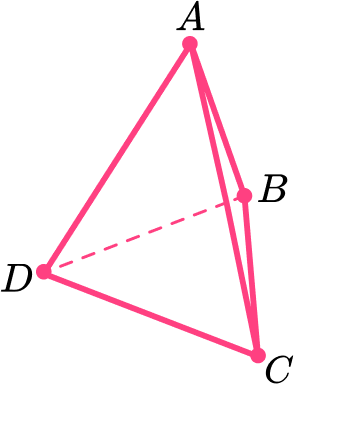
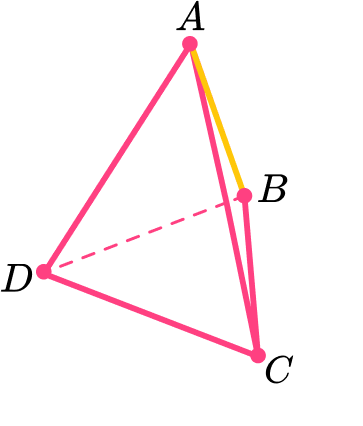
Using this labeling, you can identify lengths such as the length $AB$ :

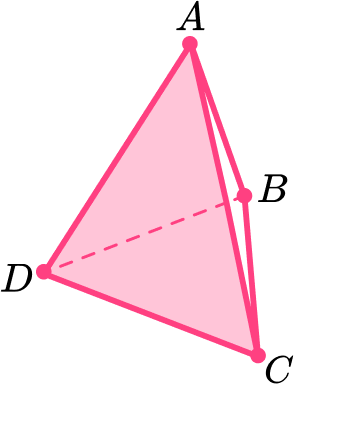
You can also identify faces such as the face $ADC$ :

A regular pyramid is when the base of a pyramid can be a different regular polygon, which results in different numbers of triangular faces that meet at the apex. This means the number of faces, edges and vertices can vary depending on the pyramid.

Let’s look at some examples of the types of pyramids:

Shape	Faces	Edges	Vertices
Triangular pyramid	$4$ All triangular	$6$	$4$
Square pyramid	$5$ $4$ triangular $1$ square	$8$	$5$
Pentagonal pyramid	$6$ $5$ triangular $1$ pentagonal	$10$	$6$
Hexagonal pyramid	$7$ $6$ triangular $1$ hexagonal	$12$	$7$

Irregular pyramids are pyramids that have an irregular polygon as a base. For example, a rectangular pyramid is considered an irregular pyramid.

You can find real life examples of pyramids. Some of the most famous real life examples of pyramids include the Louvre, a museum in Paris or the Pyramids of Egypt.

Right pyramids and oblique pyramids

A right pyramid is a type of pyramid where the vertex is directly above the center of the base. An oblique pyramid is a type of pyramid where the vertex is not directly aligned above the center of the base area.


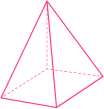Right pyramid	Oblique pyramid

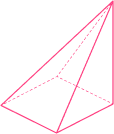To calculate the volume or surface area of a pyramid, you need to know certain lengths within the pyramid. Let’s look at each case separately.

Volume of a pyramid shape

To calculate the volume of a pyramid, use the formula:

$V=\cfrac{1}{3} \, Bh$

where:

$V$ represents the volume of the pyramid.
$B$ represents the area of the base of the pyramid.
$h$ represents the perpendicular height of the pyramid.

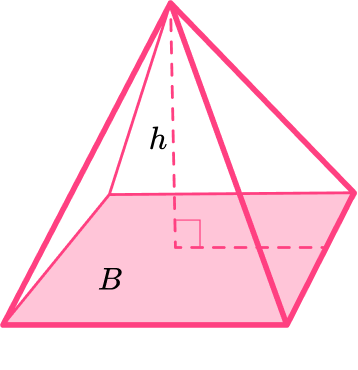
This formula can be applied to any pyramid where the base is a polygon.

For example, calculate the volume of the following square based pyramid:

\begin{aligned} V&=\frac{1}{3}\times{B}\times{h}\\ &=\frac{1}{3}\times(8\times{8})\times{9}\\ &=192\text{ cm}^{3} \end{aligned}

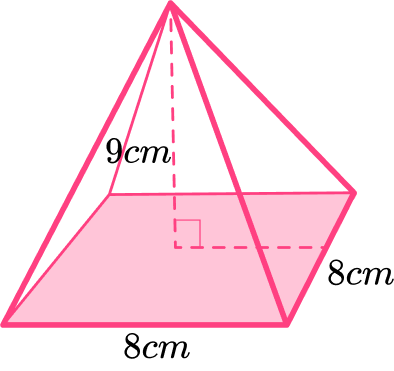
See also: Volume of a pyramid

Surface area of a pyramid shape

Since the triangular faces of a pyramid can have varying areas based on the lengths of their bases, we can still utilize our understanding of surface area to make a general statement:

The surface area of a pyramid is the total sum of the area of each face of the pyramid.

For a square based pyramid, calculate the area of the base (a square) and the area of four identical triangles:

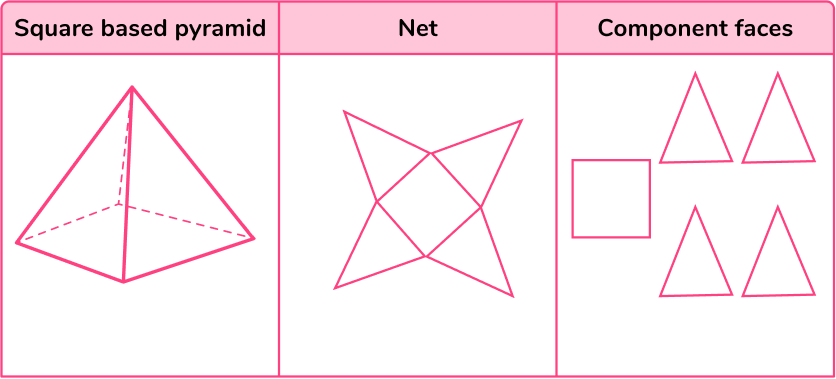
Note: you may need to calculate the missing length of a triangle using the Pythagorean theorem.

For example, calculate the surface area of the following square based pyramid, where the apex is perpendicular to the center of the base:

$\text{Area of the base }= 5\times{5}=25\text{~cm}^{2}$

$\text{Area of a triangular face }=\cfrac{1}{2}\times{6}\times{5}=15\text{~cm}^{2}$

$\text{Surface area }=25+15+15+15+15=25+(4\times{15})=85\text{~cm}^{2}.$

See also: Surface area of a pyramid

What is the pyramid shape?

Common Core State Standards

How does this relate to $1$ st grade and $7$ th grade math?

Grade 1: Geometry (1.G.A.2)
Compose two-dimensional shapes (rectangles, squares, trapezoids, triangles, half-circles, and quarter-circles) or three-dimensional shapes (cubes, right rectangular prisms, right circular cones, and right circular cylinders) to create a composite shape, and compose new shapes from the composite shape.
Grade 7: Geometry (7.G.B.6)
Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.

How to identify a pyramid shape

In order to identify a pyramid shape, you will:

Look for the characteristics of a pyramid.
State whether or not the shape is a pyramid.
If the shape is not a pyramid, explain what characteristics are different.

Pyramid shape examples

Example 1: identify a pyramid shape

Look at the image below and determine if it is a pyramid or not.

Look for the characteristics of a pyramid.

A pyramid has a polygonal base and triangular faces that meet at a point, or vertex.

This shape has an octagon for a base and triangular sides that meet at a vertex.

2State whether or not the shape is a pyramid.

This shape is a pyramid because it has a polygonal base, an octagon, and triangular faces that meet at a point, or vertex.

Example 2: identify a pyramid shape

Look at the image below and determine if it is a pyramid or not.

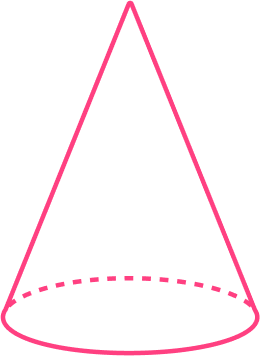
Look for the characteristics of a pyramid.

A pyramid has a polygonal base and triangular faces that meet at a point, or vertex.

This shape has a circular base that tapers smoothly to a vertex.

State whether or not the shape is a pyramid.

This shape is a cone, not a pyramid.

If the shape is not a pyramid, explain what characteristics are different.

The shape has a circular base that tapers to a vertex. It is missing the polygonal base with triangular faces.

How to calculate the volume of a pyramid shape

In order to calculate the volume of a pyramid shape:

Calculate the area of the base.
Substitute values into the formula and solve.
Write the answer, including the units.

Example 3: volume of a square-based pyramid

Calculate the volume of the square based pyramid below. Write your answer to $2$ decimal places.

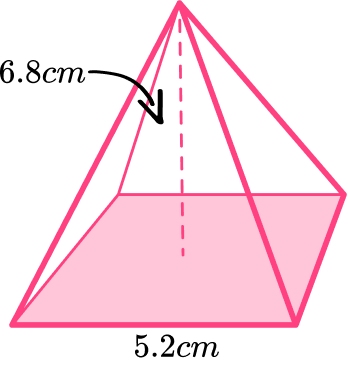
Calculate the area of the base.

The area of the base is:

$5.2\times 5.2= 27.04$

$B=27.04 {~cm}^2$

Substitute values into the formula and solve.

The formula for the volume of a pyramid is: $V=\cfrac{1}{3} \, Bh$ with $B = 27.04 {~cm}^2$ and $\, h = 6.8 {~cm}$ . Substituting these values for the base and the vertical height, you have:

$\begin{aligned} V&=\cfrac{1}{3}\times{27.04}\times{6.8}\\\\ V&=61.29066667… \end{aligned}$

Write the answer, including the units.

You will write the answer to $2$ decimal places.

$V = 61.29 \mathrm{~cm}^3$

Example 4: volume of a rectangular-based pyramid

The pyramid $ABCDE$ has a rectangular base. The apex is vertically above the center of the base. Calculate the volume of the pyramid. Write your answer to $1$ decimal place.

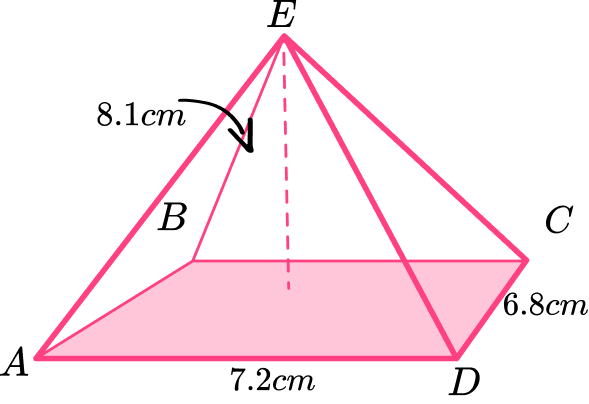
Calculate the area of the base.

The area of the base is:

$6.8\times 7.2=48.96$

$B = 48.96 {~cm}^2$

Substitute values into the formula and solve.

The formula for the volume of a pyramid is $V=\cfrac{1}{3} \, Bh$ , where $B= 48.96 {~cm}^2$ , and $\, h = 8.1 {~cm}$ . Substituting these values into the formula,

$\begin{aligned} V&=\cfrac{1}{3}\times{48.96}\times{8.1}\\\\ V&=132.192 \end{aligned}$

Write the answer, including the units.

You will write the answer to $1$ decimal place.

$V=132.2 \mathrm{~cm}^3$

How to calculate the surface area of a pyramid shape

In order to find the surface area of a pyramid shape:

Calculate the area of each face.
Add the area of each face together.
Include the units.

Example 5: finding the surface area from a 3D diagram

The polyhedron $A B C D E$ is a square based pyramid. The point $M$ lies on the edge $AD$ where $AM = MD$ . The point $E$ is perpendicular to the center of the base $A B C D$ . Calculate the surface area of the pyramid.

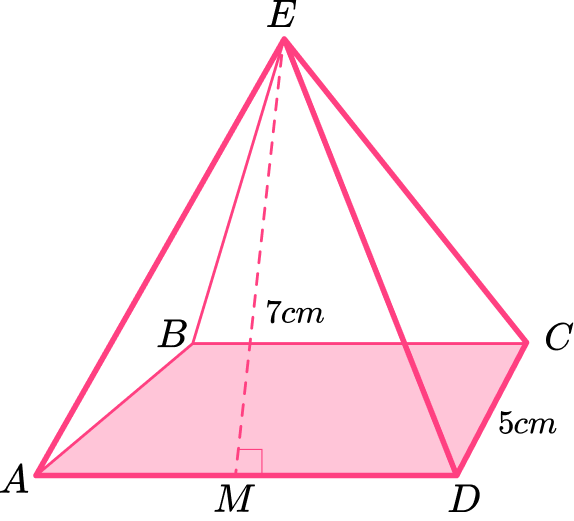
Calculate the area of the base.

The area of the base is:

$5\times 5=5^2=25$

All four triangular faces are identical and so calculate the area of one triangle, and then multiply the area by $4$ .

$\begin{aligned} A&=\cfrac{1}{2}\times{b}\times{h}\\\\ &=\cfrac{1}{2}\times{5}\times{7}\\\\ &=17.5\text{~cm}^{2} \end{aligned}$

$17.5\times{4}=70\text{~cm}^{2}$

Add the area of each face together.

Add the area of the base and the area of the four triangles:

$SA=25+70=95$

Include the units.

The side lengths are measured in centimeters, so the area is measured in square centimeters.

$SA=95\text{~cm}^{2}$

Example 6: calculating the surface area from a 3D diagram

$A B C D$ is a triangular based pyramid.

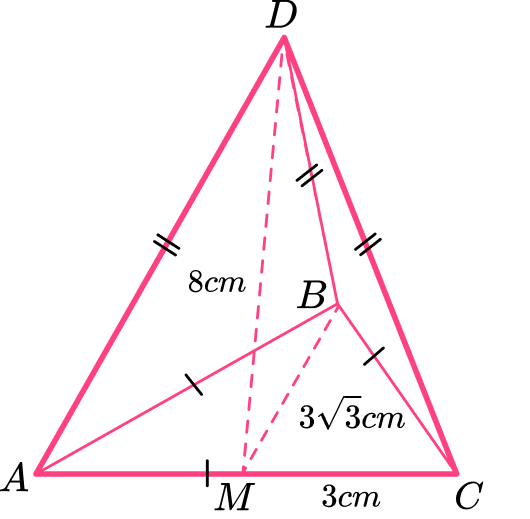
Triangle $ABC$ is equilateral. All of the other faces are congruent, isosceles triangles. The point $M$ is the midpoint of the line $AC$ such that:

$M B=3\sqrt{3} \mathrm{~cm}$
$M C=3\text{~cm}$
$M D=8\text{~cm}$

Calculate the surface area of the pyramid.

Calculate the area of the base.

The area of the base (which is a triangle) is:

$\begin{aligned} & A=\cfrac{1}{2} \times b \times h \\\\ & =\cfrac{1}{2} \times 6 \times 3\sqrt{3} \\\\ & =9\sqrt{3} \mathrm{~cm} \end{aligned}$

All three triangular faces are identical and so calculate the area of one triangle, and then multiply the area by $3$ .

$\begin{aligned} A&= \cfrac{1}{2}\times{b}\times{h}\\\\ &=\cfrac{1}{2}\times{8}\times{3}\\\\ &=12\text{~cm}^{2} \end{aligned}$

Add the area of each face together.

The total surface area is the sum of each of the four triangles:

$9\sqrt{3}+12=27.588457...$

Include the units.

The side lengths are measured in centimeters, so the area is measured in square centimeters.

$S A=27.6 \mathrm{~cm}^2$

Teaching tips for the pyramid shape

Use visual aids such as pictures, diagrams, or models of different types of pyramids to help students visualize the shape. Show examples of pyramids from different cultures and highlight their unique features.

Instead of providing practice worksheets, present problem-solving tasks or challenges related to pyramids. For example, ask students to work together to calculate the surface area or volume of a given pyramid.

Easy mistakes to make

Confusing pyramid shape with a cone
Pyramids have a polygonal base and triangular faces that meet at a single point. Cones will always have a circular base and a curved surface that meets at a vertex.

Using the wrong units when finding the surface area
The surface area will have square units such as square centimeters $\left(\mathrm{cm}^2\right)$ or square meters $\left(m^2\right)$ .

Using the wrong units when finding the volume
The volume will have cube units such as cubic centimeters $\left(\mathrm{cm}^3\right)$ or cubic meters $\left(m^3\right)$ .

Practice pyramid shape questions

Pyramid Shape image 18 US

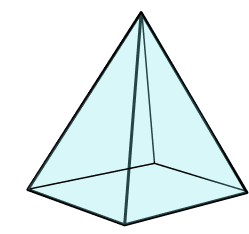
Pyramid-Shape-image-19-US

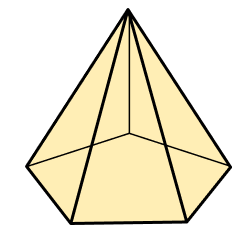
Pyramid-Shape-image-20-US

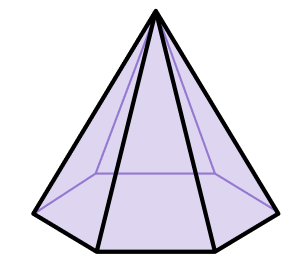
Pyramid Shape image 21 US

A square pyramid is a pyramid with a square base and $4$ triangular faces that meet at a vertex.

Pyramid-Shape-image-19-US

Pyramid Shape image 23 US

Pyramid Shape image 24 US

Pyramid Shape image 25 US

Pyramid Shape image 26 US

This shape is a rectangular pyramid, because it has a rectangle as a base with triangular faces.

A rectangle is not a regular polygon, which makes this an irregular pyramid.

630\text{~cm}^3

210\text{~cm}^3

1890\text{~cm}^3

5670\text{~cm}^3

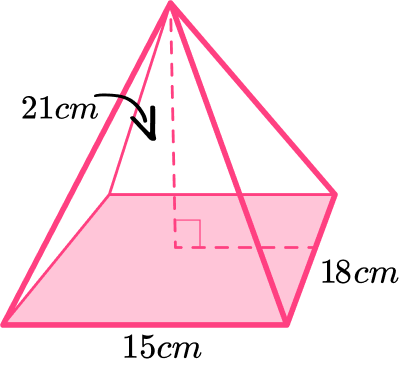
You will need to find the volume of the pyramid.

First start by finding the area of the square base:

$\begin{aligned} & B=15 \times 18 \\\\ & B=270 \mathrm{~cm}^2 \end{aligned}$

Then substitute the values into the formula, where $B=270$ and $h=21$ .

$\begin{aligned} & V=\cfrac{1}{3} \times B \times h \\\\ & =\cfrac{1}{3} \times 270 \times 21 \\\\ & =1890 \mathrm{~cm}^3 \end{aligned}$

4{~cm}

10{~cm}

8{~cm}

12{~cm}

Start by substituting the known values into the volume formula.

$\begin{aligned} & V=\cfrac{1}{3} \times B \times h \\\\ & 160=\cfrac{1}{3} \times 40 \times h \end{aligned}$

You will divide both sides of the equation by $\cfrac{1}{3}$ .

$480=40 \times h$

Finally, divide both sides of the equation by $40$ .

$h=12 \mathrm{~cm}$

48 \text{~cm}^2

128 \text{~cm}^2

80 \text{~cm}^2

64 \text{~cm}^2

$\text{Base }=4\times{4}=16\text{~cm}^{2}$

$\text{Triangular faces }=(\cfrac{1}{2}\times{8}\times{4})\times{4}=64\text{~cm}^{2}$

$SA=16+64=80\text{~cm}^{2}$

61.4 \text{~cm}^2

68.89 \text{~cm}^2

157.7 \text{~cm}^2

246.51 \text{~cm}^2

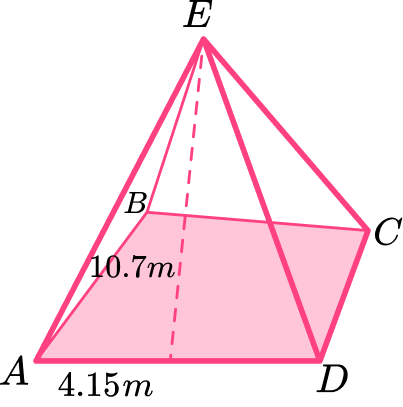
You will find the surface area of a square pyramid, so you’ll need to find the total sum of the area of each pyramid.

First find the area of the base:

$\text {Area of the base }=(4.15 \times 2)^2 \mid$

Then find the area of the triangular faces:

$\text {Area of the triangular face }=\left(\cfrac{1}{2} \times 10.7 \times 8.3\right) \times 4$

Add the area of the square base and the triangular faces together, and round to two decimal places.

$\begin{aligned} & =68.89+177.62 \\\\ & =246.51 \mathrm{~cm}^2 \end{aligned}$

Pyramid shape FAQs

What are the different types of pyramids?

Some of the different types of pyramids are triangular pyramids, including equilateral triangle pyramids, square pyramids, pentagonal pyramids, hexagonal pyramids and octagonal pyramids. Pyramids can have regular or irregular polygons as bases.

Is a cone a pyramid?

A circle is not a polygon as a polygon has a finite number of edges, connected by vertices. As a pyramid has a polygonal base, the base cannot be a circle as a circle is not a polygon. So, a cone is not a pyramid.

Are the Pyramids of Egypt examples of regular pyramids?

Yes, the Egyptian pyramids are examples of regular pyramids. The Great Pyramid of Giza is an example of a triangular pyramid and The Pyramid of Djoser is an example of a square pyramid.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.