[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!!
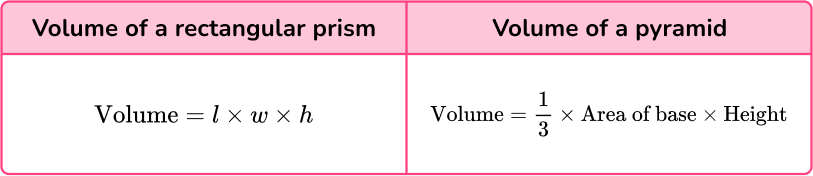
Volume formula
Here you will learn about volume formulas, including the formula for calculating the volume of 3D shapes and how to use the volume formula to solve problems.
Students will first learn about the volume formula as part of measurement and data in the 5 th grade, and continue to expand on their knowledge in geometry in the 6 th and 7 th grade.
What is a volume formula?
A volume formula is a formula which is used to calculate the volume of a 3D shape.
Volume is the amount of space there is inside a shape.
To calculate the volume of an object in three dimensions, you can use the various volume formulas.
| Cube |  | \text { Volume }=a^3 |
|---|---|---|
| Rectangular prism | 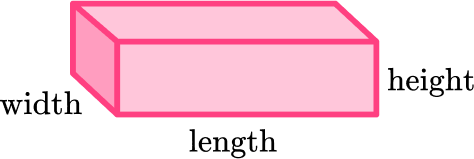 | \text{Volume}=l\times w\times h |
| Prism | 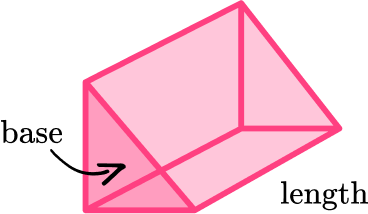 | \text{Volume}=\text{Area of base} \times \text{Length} |
| Cylinder |  | \text{Volume}=\pi r^2h (\text { Volume }=\text { Area of base } \times \text { Height } ) |
| Pyramid | 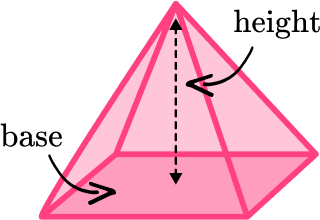 | \text{Volume}=\cfrac{1}{3} \, \times \text{Area of base} \times \text{Height} |
| Cone |  | \text{Volume}=\cfrac{1}{3} \, \pi r^2h (\text{Volume}=\cfrac{1}{3} \, \times \text{Area of base} \times \text{Height}) |
| Sphere |  | \text{Volume}=\cfrac{4}{3} \, \pi r^3 |
Volume is measured in cubic units.
- Customary units examples
- ft^3- cubic feet
- \mathrm{in}^3- cubic inches
- Metric units examples
- \mathrm{cm}^3 - cubic centimeters
- m^3 - cubic meters
- \mathrm{mm}^3 - cubic millimeters
Volume can also be described using units of capacity such as milliliters, liters, pints or gallons.
What is a volume formula?
Common Core State Standards
How does this relate to 5th, 6 th and 7 th grade math?
- Grade 5: Measurement and Data (5.MD.C.5b)
Apply the formulas V = l \times w \times h and V = b \times h for rectangular prisms to find volumes of right rectangular prisms with whole number edge lengths in the context of solving real world and mathematical problems.
- Grade 6: Geometry (6.G.A.2)
Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes of the appropriate unit fraction edge lengths, and show that the volume is the same as would be found by multiplying the edge lengths of the prism.
Apply the formulas V = l \times w \times h and V = b \times h to find volumes of right rectangular prisms with fractional edge lengths in the context of solving real-world and mathematical problems.
- Grade 7: Geometry (7.G.B.6)
Solve real-world and mathematical problems involving area, volume, and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
- Grade 8: Geometry (8.G.C.9)
Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.
How to use volume formula
In order to use volume formula:
- Write down the formula.
- Substitute the values into the formula.
- Calculate the volume of the shape.
- Write the answer, including the units.
![[FREE] End of Year Math Assessments (Grade 4 & Grade 5)](https://thirdspacelearning.com/wp-content/uploads/2023/02/end-of-year-math-assessment-grade-4-grade-5.png)
[FREE] End of Year Math Assessments (Grade 4 & Grade 5)
Assess math progress for the end of grade 4 and grade 5 or prepare for state assessments with these mixed topic, multiple choice questions and extended response questions!
DOWNLOAD FREE [FREE] End of Year Math Assessments (Grade 4 & Grade 5)
Assess math progress for the end of grade 4 and grade 5 or prepare for state assessments with these mixed topic, multiple choice questions and extended response questions!
DOWNLOAD FREEVolume formula examples
Example 1: volume of a cylinder
Calculate the volume of the cylinder below.
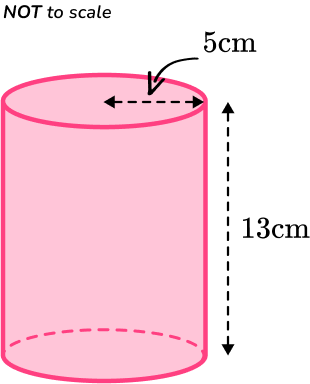
- Write down the formula.
The 3D shape is a cylinder. The formula you need to use is \text{Volume}=\pi r^2h.
2Substitute the values into the formula.
Calculate the area of a circle (the circular base) and then multiply it by the height of the shape.
The values you need to substitute into the formula are the radius of the base (r=5) and the height of the shape (h=13).
\begin{aligned} \text{Volume}&=\pi r^2h \\\\ &=\pi \times 5^2 \times 13 \end{aligned}
3Calculate the volume of the shape.
V=325 \, \pi=1021.017…
4Write the answer, including the units.
The dimensions of the cylinder were given in centimeters, so the volume (the amount of three-dimensional space inside the shape) will be in cubic centimeters (cm^3).
V=1021 \ cm^3 (to the nearest integer)
Example 2: volume of a sphere
Calculate the volume of a sphere with a diameter of 9 \, mm.
Write down the formula.
The 3D shape is a sphere. The formula you need to use is \text{Volume}=\cfrac{4}{3} \, \pi r^3.
Substitute the values into the formula.
You need to substitute the value of the radius of the sphere into the formula. You need to divide the diameter by 2 to calculate the radius r.
r=9\div 2=4.5
\begin{aligned} \text{Volume}&=\cfrac{4}{3} \, \pi r^3 \\\\ &=\cfrac {4}{3}\times \pi \times 4.5^3\end{aligned}
Calculate the volume of the shape.
V=\cfrac{243}{2} \, \pi=381.703…
Write the answer, including the units.
The dimensions of the sphere were given in millimeters, so the volume of the sphere will be in cubic millimeters (mm^3).
V=382 \ mm^3 (to the nearest integer)
Example 3: missing dimension
The volume of the rectangular prism is 2,016 \mathrm{~cm}^3.
Calculate the value of x.
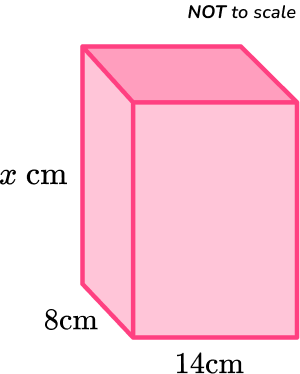
Write down the formula.
The 3D shape is a rectangular prism. The formula you need to use is
\text{Volume}=l \times w \times h.
Substitute the values into the formula.
The length (l), the width (w) and the height (h) of the rectangular prism are interchangeable, so it doesn’t matter which dimension l or w or h.
The values you need to substitute into the formula are \text{Volume}=2,016, l=8 and w=14.
For the height (h) you can use x.
\begin{aligned} \text{Volume}&=l\times w\times h \\\\ 2,016&=8 \times 14\times x \\\\ 2,016&=112\times x \end{aligned}
Calculate the volume of the shape.
In this case, you already know the volume. You divide the volume by the area of the base to find the missing height.
x=2,016\div 112=18.
Write the answer, including the units.
The dimensions of the rectangular prism were given in centimeters and the volume was given in cubic centimeters (cm^3).
Since x is a dimension of the rectangular prism, it is recorded in just units, not units cubed.
x=18 \, cm
Example 4: missing dimension
The volume of the square pyramid is 66,000 \mathrm{~cm}^3.
Calculate the height of the pyramid.
Write down the formula.
The 3D shape is a pyramid. The formula you need to use is,
\text{Volume}=\cfrac{1}{3} \times \text{Area of base} \times \text{Height}.
Substitute the values into the formula.
First, you need to calculate the area of the square base: 60^2=60\times 60=3,600.
The values you need to substitute into the formula are \text{Volume}=66, 000 and \text{Area of base}=3,600.
For the height, you can use h.
\begin{aligned} \text{Volume}&=\cfrac{1}{3}\times \text{Area of base} \times \text{Height}\\\\ 66,000&=\cfrac {1}{3}\times 3,600\times h\\\\ 66,000&=1,200\times h \end{aligned}
Calculate the volume of the shape.
In this case, you already know the volume. You divide the volume by the area of the base to find the missing height.
h=66,000\div 1,200=55.
Write the answer, including the units.
The dimensions of the pyramid were given in centimeters and the volume was given in cubic centimeters (cm^3).
Since h is a dimension of the square pyramid, it is recorded in just units, not units cubed.
h=55 \, cm
Example 5: volume of a compound shape
This shape is made from a rectangular prism and a square based pyramid. Calculate the volume of the 3D shape.
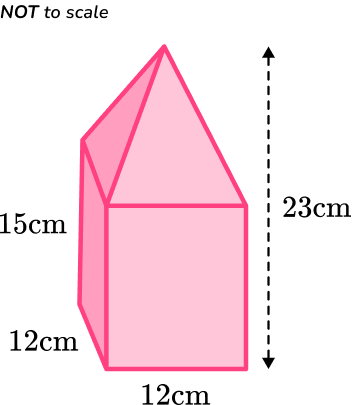
Write down the formula.
The 3D shape is made from a rectangular prism and a pyramid. Find the volume of each piece and then add the two volumes together. The formulas you need to use are:
Substitute the values into the formula.
The values you need to substitute into the formulae are
Calculate the volume of the shape.
The volume of the shape is:
\text{Total Volume}=2,160+384=2,544.
Write the answer, including the units.
The dimensions of the 3D shape were given in centimeters, so the volume will be in cubic centimeters (cm^3).
V=2,544 \, cm^3
Example 6: volume of a compound shape
This shape is made from a cylinder and a cone. Calculate the volume of the 3D shape.
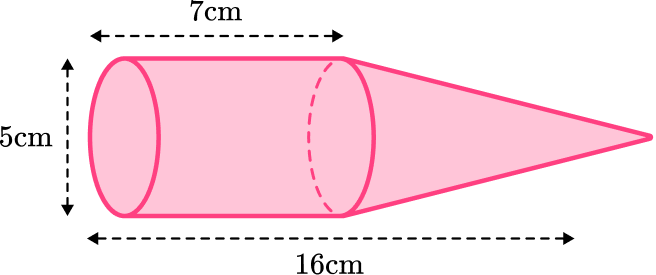
Write down the formula.
The 3D shape is made from a cylinder and a cone. You can find the volume of each piece and then add the two volumes together. The formulas you need to use are:
Substitute the values into the formula.
You need to divide the diameter by 2 to calculate the radius. The values you need to substitute into the formula are:
Calculate the volume of the shape.
The volume of the shape is:
\text{Total Volume}=\cfrac{175}{4} \, \pi+\cfrac{75}{4} \, \pi=\cfrac{125}{2} \, \pi.
Write the answer, including the units.
The dimensions of the 3D shape were given in centimeters, so the volume will be in cubic centimeters (cm^3).
V=\cfrac{125}{2} \, \pi\ cm^3 (in terms of \pi)
or
196.3 \, cm^3 (to 1 decimal place)
Teaching tips for the volume formula
- Conduct interactive demonstrations to illustrate how volume formulas work. Find the volume of water or sand using different containers of varying shapes and sizes, by asking students to estimate and calculate the volume.
- Offer a wide range of exercises and problems for students to practice calculating volume. Provide different shapes and sizes to challenge them and encourage critical thinking.
- Regularly assess students’ understanding of volume formulas through quizzes, worksheets, or project assignments. Provide timely and constructive feedback to address any misconceptions or errors.
Easy mistakes to make
- Forgetting to use units, or using the incorrect units
You should always include units in your answer.
Volume is measured in cubic units (for example, mm^3, cm^3, m^3 ).
- Calculating with different units
You need to make sure all measurements are in the same units before calculating the volume. (For example, you can’t have some measurements in centimeters and some in meters).
- Using the wrong formula when calculating volume
Be careful to make sure you use the correct formula for the volume of the three-dimensional shape. Volume formulas can be easily confused with each other and with formulas for calculating the surface area of a three-dimensional object.
Related volume lessons
Practice volume formula questions
1. Calculate the volume.
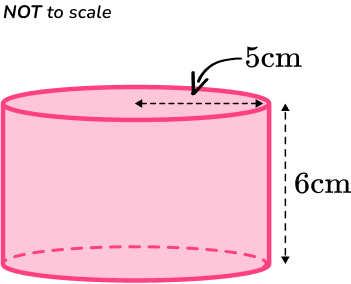
The volume formula to calculate the volume of the cylinder is \text{Volume} =\pi r^2h.
You need to substitute in the values r=5 and h=6.
\begin{aligned}\text{Volume} &=\pi r^2h \\\\ &= \pi \times 5^2 \times 6 \\\\ &=150 \, \pi \\\\ &=471.23…\end{aligned}
The volume of the cylinder is 471 \, cm^3.
2. Calculate the volume of this pyramid.
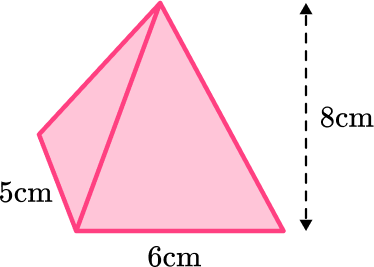
The volume formula to calculate the volume of the pyramid is \text{Volume} =\cfrac{1}{3}\times \text{Area of base}\times \text{Height}.
You need to find the area of the base of the pyramid.
A=5\times 6=30
\begin{aligned}\text{Volume} &=\cfrac{1}{3}\times \text{area of base}\times \text{height} \\\\ &= \cfrac{1}{3}\times 30\times 8 \\\\ &=80\end{aligned}
The volume of the pyramid is 80 \, cm^3.
3. The volume of this is 720 \, mm^3. Calculate the length of the missing side.
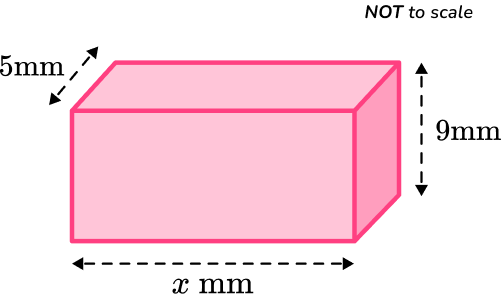
The volume formula to calculate the volume of the rectangular prism is \text{Volume} =l\times w\times h.
You need to substitute in the values given, using x for the unknown length, into the volume formula.
\begin{aligned}\text{Volume} &=l\times w\times h\\\\ 720&=x\times 5\times 9\\\\ 720&=x\times 45\end{aligned}
The missing length is x=720\div 45=16.
The missing length of the rectangular prism is 16 \, mm.
4. The volume of a cylinder is 160 \, \pi \, cm^3. The height of the cylinder is 6.4 \, cm. Find the radius of the cylinder.
The volume formula to calculate the volume of the cylinder is \text{Volume} =\pi r^2h.
You need to substitute in the values given into the formula:
\begin{aligned}\text{Volume} &=\pi r^2h.\\\\ 160 \, \pi&=\pi \times r^2\times 6.4 \end{aligned}
Solve for the missing length:
\begin{aligned}r^2&=\cfrac{160 \, \pi}{\pi \times 6.4}\\\\ r^2&=25 \; \text{(think about what number times itself is 25.}) \\\\ r&=5, \text{because} \; 5 \times 5 = 25. \end{aligned}
The radius of the cylinder is 5 \, cm.
5. Calculate the volume of the shape below.
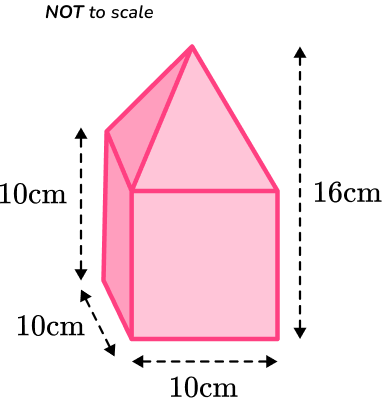
The volume of the rectangular prism is:
\begin{aligned}\text{Volume}&=l\times w\times h\\\\ &=10\times 10\times 10\\\\ &=1,000\end{aligned}
Or you can take one side of the cube and cube it.
10^3=1,000
The volume of the pyramid is
\begin{aligned}\text{Volume}&=\cfrac{1}{3}\times \text{area of base}\times \text{height}\\\\ &=\cfrac{1}{3}\times 10\times 10\times 6\\\\ &=200\end{aligned}
The total volume can be found by adding the two volumes together.
\text{Total Volume}=1,000+200=1,200 \, cm^3
6. Calculate the volume of the shape below.
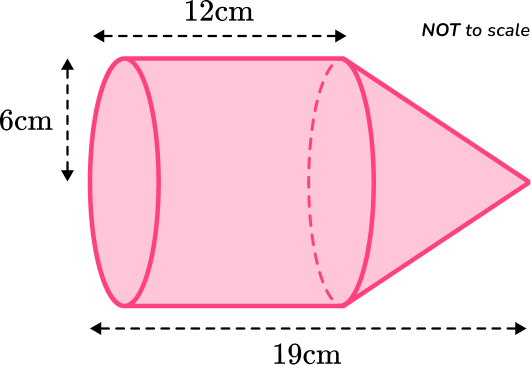
The volume of the cylinder is:
\begin{aligned}\text{Volume}&=\pi r^2h\\\\ &=\pi \times 6^2\times 12\\\\ &=432 \, \pi \end{aligned}
The volume of the cone is:
\begin{aligned}\text{Volume}&=\cfrac{1}{3} \, \pi r^2h\\\\ &=\cfrac{1}{3}\times \pi \times 6^2\times 7\\\\ &=84 \, \pi\end{aligned}
The total volume can be found by adding the two volumes together.
\text{Total Volume}=432 \, \pi+84 \, \pi=516 \, \pi \, cm^3
Volume formula FAQs
The formula for calculating the volume of a triangular prism is V=\cfrac{1}{2} \, B \times h , where "V" represents the volume, "B" represents the area of the triangular base, and "h" represents the height of the prism.
No, cuboid is another word for a rectangular prism.
The base is always the two congruent opposite polygons, not just the bottom. The bases are connected by the lateral faces, which is why they are the height, even if the prism is laying on its side.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.