Volume of a Cylinder - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Volume Volume formula Volume of a prism Volume of a cube

Math resources Geometry Volume

Volume of a cylinder

Here you will learn about the volume of a cylinder, including how to calculate the volume of a cylinder given its radius, area and perpendicular height.

Students will first learn about volume of cylinders as part of geometry in grade $7$ and again in grade $8$ and high school geometry.

What is the volume of a cylinder?

The volume of a cylinder is the amount of space there is inside a cylinder.

In order to find the volume of a cylinder you first need to find the circular area of the base.

To do this, you can use the formula for calculating the area of a circle, which is

\text { Area }=\pi r^2.

Then multiply the area of the circular base by the height (or length) of the cylinder.

To do this, you can use the formula for the volume of a cylinder, which is

\text { Volume }=\pi r^2 h.

Where $\textbf{r}$ is the radius of a cylinder and $\textbf{h}$ is the perpendicular height of a cylinder.

For example, find the volume of this cylinder with radius of the base $7~cm$ and perpendicular height $10~cm.$

\begin{aligned} & \text { Volume }=\pi r^2 h \\\\ & =\pi \times 7^2 \times 10 \\\\ & =490 \pi \\\\ & =1539.380 \ldots \\\\ & =1539.4 \mathrm{~cm}^3 \; (\text {to } 1 \; \mathrm{dp}) \end{aligned}

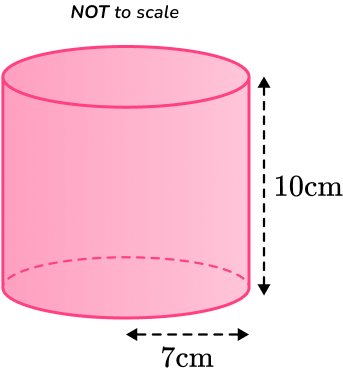
What is the volume of a cylinder?

Common Core State Standards

How does this relate to $7$ th grade and high school math?

Grade 7 – Geometry (7.G.B.6)
Solve real-world and mathematical problems involving area, volume and total surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.

High School – Geometry (HSG.GMD.A.3)
Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.

[FREE] Volume Check for Understanding Quiz (Grade 6 to 8)

Use this quiz to check your grade 6 to 8 students’ understanding of volume. 10+ questions with answers covering a range of 6th, 7th and 8th grade volume topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Volume Check for Understanding Quiz (Grade 6 to 8)

DOWNLOAD FREE

How to calculate the volume of a cylinder

Write down the formula: $\text{Volume} = \pi r^2 h$
Substitute the given values.
Work out the calculation.
Write the final answer, including units.

Volume of a cylinder examples

Example 1: volume of a cylinder

Find the volume of the cylinder with radius $3~cm$ and perpendicular height $5~cm.$

Give your answer to $1$ decimal place.

Write down the formula.

To answer the question you need the formula for the volume of a cylinder.

\text { Volume }=\pi r^2 h

2Substitute the given values.

Substitute the value of the radius $r$ and the perpendicular height $h$ into the formula.

V=\pi \times 3^2 \times 5

3Work out the calculation.

Use a calculator to work out the volume.

V=45 \pi=141.371

4Write the final answer, including units.

Check what form the final answer needs to be written in. You may need to leave your answer in terms of $\pi$ or as a decimal with rounding. Here you are asked to give the answer to $1$ decimal place.

V=141.371=141.4 \mathrm{~cm}^3

The volume of the cylinder is: $141.4 \mathrm{~cm}^3.$

Example 2: volume of a cylinder

Find the volume of the cylinder with radius $4.8~cm$ and perpendicular height $7.9~cm.$

Give your answer to $3$ significant figures.

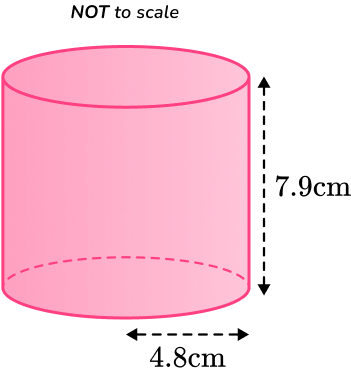
Write down the formula.

To answer the question you need the formula for the volume of a cylinder.

$\text { Volume }=\pi r^2 h$

Substitute the given values.

Substitute the value of the radius $r$ and the perpendicular height $h$ into the formula.

$V=\pi \times 4.8^2 \times 7.9$

Work out the calculation.

Use a calculator to work out the volume.

$V=571.820$

Write the final answer, including units.

Check what form the final answer needs to be.

You may need to leave your answer in terms of $\pi$ or as a decimal with rounding.

Here you are asked to give the answer to $3$ significant figures.

$V=571.820=572 \mathrm{~cm}^3$

The volume of the cylinder is: $572 \mathrm{~cm}^3.$

Example 3: volume of a cylinder

Find the volume of the cylinder with radius $3~cm$ and perpendicular height $7~cm.$

Leave your answer in terms of $\pi.$

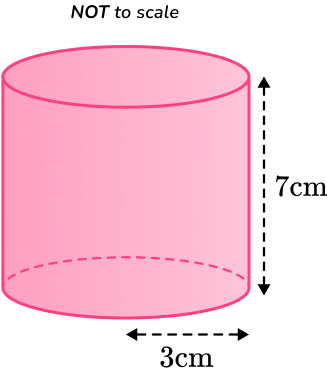
Write down the formula.

To answer the question you need the formula for the volume of a cylinder.

$\text { Volume }=\pi r^2 h$

Substitute the given values.

Substitute the value of the radius $r$ and the perpendicular height $h$ into the formula.

$V=\pi \times 3^2 \times 7$

Work out the calculation.

Work out the volume. (Focusing on the number parts of the calculation).

$V=63 \pi$

Write the final answer, including units.

Check what form the final answer needs to be written in. You may need to leave your answer in terms of $\pi$ or as a decimal with rounding.

$V=63 \pi=63 \pi \mathrm{~cm}^3$

The volume of the cylinder is: $63 \pi \mathrm{~cm}^3.$

Example 4: volume of a cylinder

Find the volume of the cylinder with radius $4~cm$ and perpendicular height $10~cm.$

Leave your answer in terms of $\pi.$

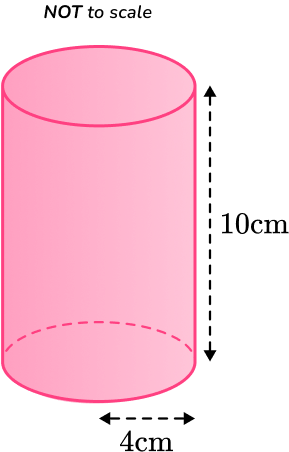
Write down the formula.

To answer the question you need the formula for the volume of a cylinder.

$\text { Volume }=\pi r^2 h$

Substitute the given values.

Substitute the value of the radius $r$ and the perpendicular height $h$ into the formula.

$V=\pi \times 4^2 \times 10$

Work out the calculation.

Work out the volume. (Focusing on the number parts of the calculation).

$V=160 \pi$

Write the final answer, including units.

Check what form the final answer needs to be.

You may need to leave your answer in terms of $\pi$ or as a decimal with rounding.

$V=160 \pi=160 \pi \mathrm{~cm}^3$

The volume of the cylinder is: $160 \pi \mathrm{~cm}^3.$

Example 5: using the formula to find a length

The volume of a cylinder is $1600~cm^3.$ Its radius is $9~cm.$ Find its perpendicular height. Give your answer to $2$ decimal places.

Write down the formula.

The question involves the volume of a cylinder, so you need the formula for the volume of a cylinder.

$V=\pi r^2 h$

Substitute the given values.

You are given the volume and the radius, so substitute these into the formula.

$1600=\pi \times 9^2 \times h$

Work out the calculation.

You need to rearrange the formula to find the value of $h.$

$1600=\pi \times 81 \times h$

$\cfrac{1600}{\pi \times 81}=h$

$h=6.287$

Write the final answer, including units.

Check what form the final answer needs to be.

You may need to leave your answer in terms of $\pi$ or as a decimal with rounding.

Here you are asked to give the answer to $2$ decimal places.

$h=6.287=6.29 \mathrm{~cm}$

The perpendicular height of the cylinder is: $6.29~cm.$

Example 6: using the formula to find a length

The volume of a cylinder is $1400~cm^3.$ Its perpendicular height is $15~cm.$ Find its radius. Give your answer to $2$ decimal places.

Write down the formula.

The question involves the volume of a cylinder, so you need the formula for the volume of a cylinder.

$V=\pi r^2 h$

Substitute the given values.

You are given the volume and the perpendicular height, so substitute these into the formula.

$1400=\pi \times r^2 \times 15$

Work out the calculation.

You need to rearrange the formula to find the value of $h.$

$1400=\pi \times r^2 \times 15$

$\cfrac{1400}{\pi \times 15}=r^2$

$r^2=29.70892$

$r=\sqrt{29.70892}$

Write the final answer, including units.

Check what form the final answer needs to be written in.

You may need to leave your answer in terms of $\pi$ or as a decimal with rounding.

Here you are asked to give the answer to $2$ decimal places.

$r=\sqrt{29.70892}=5.4505=5.45 \mathrm{~cm}$

The radius of the cylinder is: $5.45~cm.$

Teaching tips for volume of a cylinder

Implement engaging visual aids and real-world examples to illustrate how the formula applies, fostering a deeper comprehension of $3d$ shapes. Using visual aids will also help English Language Learners comprehend the complexity of the three dimensional space and three-dimensional shapes.

Incorporate interactive activities and group exercises that encourage hands-on exploration of cylinder volume calculations, ensuring students actively participate in the learning process. Incorporating open-ended tasks for students to find the surface area of a cylinder, cuboid, or oblique cylinder as well as a focus on the area of the cylinder and base of the cylinder will scaffold student learning appropriately.

Provide step-by-step problem-solving tutorials, addressing common challenges students might encounter when finding the volume of a cylinder, thereby enhancing the accessibility and usefulness of your educational content.

Highlight the importance of exposing students to diverse cubic units such as cubic inches, cubic centimeters, cubic meters, and cubic feet, as it not only reinforces the concept of volume but also fosters a versatile and practical comprehension of three-dimensional space.

Easy mistakes to make

Incorrect radius calculation
When finding the volume of a cylinder, be cautious not to miscalculate the radius, as errors in this fundamental measurement can lead to inaccuracies in the final volume. Emphasize the importance of doubling the radius squared and verify calculations to prevent mistakes.

Misinterpreting height measurements
Avoid the mistake of misinterpreting or inaccurately measuring the height of the cylinder. Stress the need for precision in obtaining height values, and remind students to double-check measurements to ensure accuracy in volume calculations.

Omitting units in the final answer
In the excitement of solving volume problems, it’s easy to overlook including the appropriate units in the final answer. Remind students to always attach the correct cubic units (cubic inches, cubic centimeters, cubic feet, cubic meters, etc.) to their volume results, enhancing clarity and correctness.

Neglecting the order of operations
Students may inadvertently neglect the proper order of operations when applying the volume formula. Reinforce the importance of parentheses and guiding students to follow the correct sequence to prevent errors in their calculations.

Overlooking the $\textbf{P}\,\textbf{i}$ value
Students may forget to incorporate the value of $Pi$ accurately, leading to significant errors in volume calculations. Stress the consistent use of the correct $\pi$ value and caution against rounding too early in the calculation process to maintain precision in results.

Practice volume of a cylinder questions

293 \mathrm{~cm}^3

292 \mathrm{~cm}^3

832 \mathrm{~cm}^3

833 \mathrm{~cm}^3

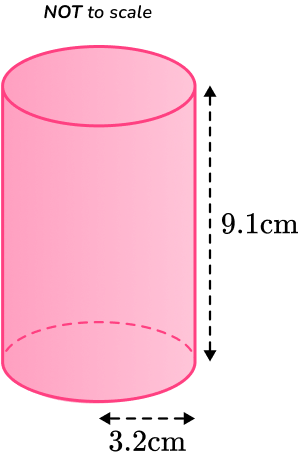
You are finding the volume of a cylinder so substitute the value of $r$ and $h$ into the formula.

\begin{aligned} V&=\pi r^2 h\\\\ V&=\pi \times 3.2^2 \times 9.1\\\\ V&=292.746\\\\\ V&=293 \ cm^3 \end{aligned}

336 \mathrm{~cm}^3

240 \mathrm{~cm}^3

241 \mathrm{~cm}^3

335 \mathrm{~cm}^3

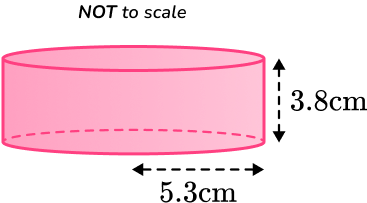
You are finding the volume of a cylinder so substitute the value of $r$ and $h$ into the formula.

\begin{aligned} V&=\pi r^2 h\\\\ V&=\pi \times 5.3^2 \times 3.8\\\\ V&=335.339\\\\ V&=335 \ cm^3 \end{aligned}

446 \pi \mathrm{~cm}^3

444 \pi \mathrm{~cm}^3

448 \pi \mathrm{~cm}^3

442 \pi \mathrm{~cm}^3

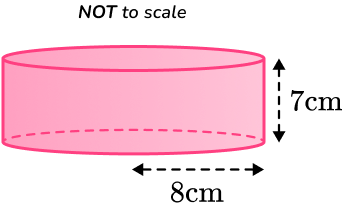
You are finding the volume of a cylinder so substitute the value of $r$ and $h$ into the formula.

\begin{aligned} V&=\pi r^2 h\\\\ V&=\pi \times 8^2 \times 7\\\\ V&=448\pi\\\\ V&=448\pi \ cm^3 \end{aligned}

402 \mathrm{~cm}^3

336 \mathrm{~cm}^3

240 \mathrm{~cm}^3

241 \mathrm{~cm}^3

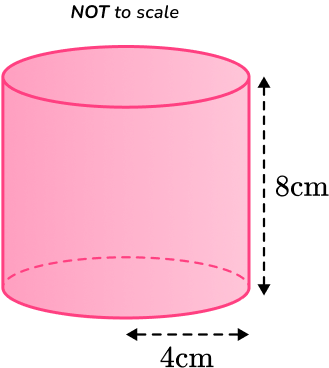
You are finding the volume of a cylinder so substitute the value of $r$ and $h$ into the formula.

\begin{aligned} V&=\pi r^2 h\\\\ V&=\pi \times 4^2 \times 8\\\\ V&=402.1238 \\\\\ V&=402 cm^3 \end{aligned}

9.43 \mathrm{~cm}

9.46 \mathrm{~cm}

9.44 \mathrm{~cm}

9.45 \mathrm{~cm}

Using the formula, substitute the value of the volume and the value of the radius and rearrange to find the radius.

\begin{aligned} V&=\pi r^2 h \\\\ 250&=\pi \times 2.9^2 \times h\\\\ \cfrac{250}{\pi \times 2.9^2}\,&=h\\\\ h&=9.4622\\\\ h&=9.46 \ cm \end{aligned}

5.26 \mathrm{~cm}

5.24 \mathrm{~cm}

5.25 \mathrm{~cm}

5.27 \mathrm{~cm}

Using the formula, substitute the value of the volume and the value of the perpendicular height and rearrange to find the radius.

\begin{aligned} V&=\pi r^2 h\\\\ 800&=\pi \times r^2 \times 9.2\\\\ \cfrac{800}{\pi \times 9.2}\,&=r^2\\\\ r&=\sqrt{\cfrac{800}{\pi \times 9.2}}\\\\ r&=5.2610\\\\ r&=5.26 \ cm \end{aligned}

Volume of a cylinder FAQs

What are common mistakes to avoid when finding the volume of a cylinder?

Common mistakes include misinterpreting height measurements, miscalculating the radius, and omitting units. Learn to recognize and avoid these errors for accurate volume calculations. Additionally, double-check your calculations and ensure you follow the correct order of operations.

Are there different units I can use for cylinder volume calculations?

Yes, you can use various cubic units, such as cubic inches or cubic centimeters, when calculating cylinder volume. Understanding different units provides versatility in solving real-world problems. Be consistent with your unit usage to maintain precision in your answers.

How can I ensure I include the correct $Pi$ value in cylinder volume calculations?

Ensure accuracy by consistently using the appropriate $Pi$ value throughout your calculations. Maintain precision by avoiding premature rounding in the process. Remember to keep $\pi$ in your calculations until the final step for accurate results.

What are practical examples to better understand cylinder volume calculations?

Engage in hands-on activities like measuring the volume of cylindrical objects such as cans or jars. These real-world examples enhance your grasp of the volume formula and its applications. Experiment with various objects to reinforce the concept and its practical implications in different scenarios.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.