Surface Area of a Sphere - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Parts of a circle

Sphere shape Math formulas Rounding Multiplication and division

Math resources Geometry Surface area

Surface area of a sphere

Here you will learn about the surface area of a sphere, including how to calculate the surface area of a sphere given its radius and the surface area of a hemisphere.

Students will first learn about the surface area of a sphere as a part of geometry in $8$ th grade.

What is the surface area of a sphere?

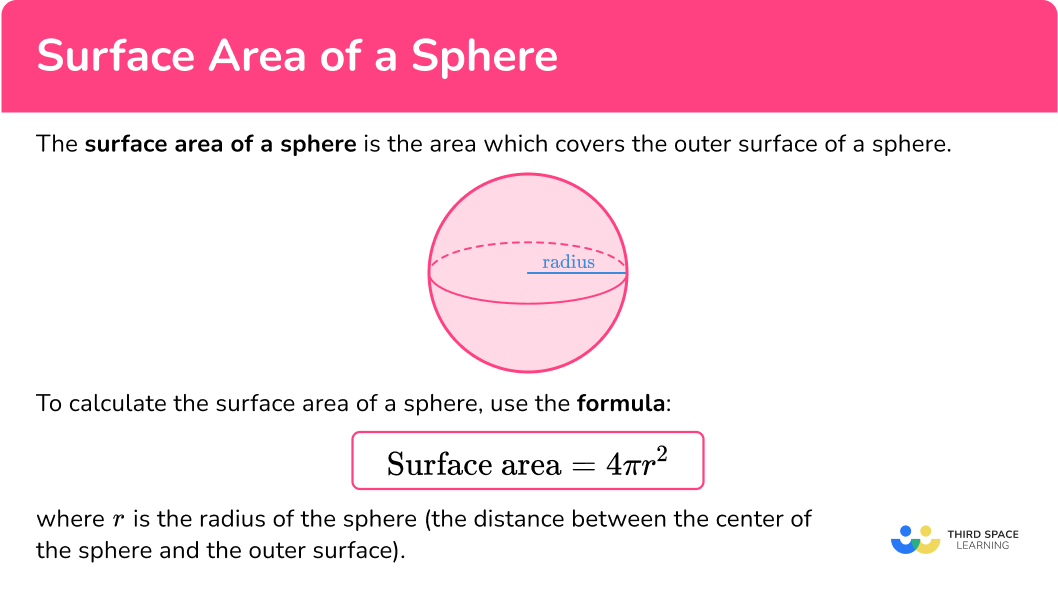
The surface area of a sphere is the area which covers the outer surface of the sphere. It includes both the curved surface area of a sphere and the area of the sphere’s circular base, also known as the total surface area of a sphere (tsa).

The formula for the surface area of a sphere with radius $r$ is:

$\text{Surface area}=4\pi{r}^{2}$

Notice that the square of the radius $(r^2)$ occurs within the surface area formula.

The surface area of a shape uses two-dimensions, so the units for surface area are units squared.

What is the surface area of a sphere?

Common Core State Standards

How does this relate to $8$ th grade math?

Grade 8: Geometry (8.G.C.9)
Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.

[FREE] Surface Area Worksheet (Grade 6)

Use this quiz to check your grade 6 students’ understanding of surface area. 10+ questions with answers covering a range of 6th grade surface area topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Surface Area Worksheet (Grade 6)

Use this quiz to check your grade 6 students’ understanding of surface area. 10+ questions with answers covering a range of 6th grade surface area topics to identify areas of strength and support!

DOWNLOAD FREE

How to calculate the surface area of a sphere

In order to calculate the surface area of a sphere:

Write down the formula.
Substitute the given values into the formula.
Complete the calculation.
Write the final answer, including the units.

Surface area of a sphere examples

Example 1: surface area of a sphere given the radius

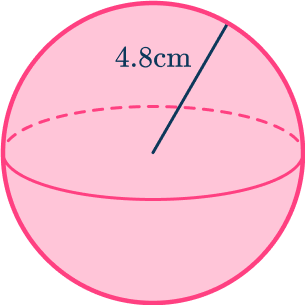
Find the surface area of the sphere below. Write your answer to $1$ decimal place.

Write down the formula.

To answer the question, use the formula for the surface area of a sphere:

\text{Surface area}=4 \pi r^2

2Substitute the given values into the formula.

The radius (the distance from the center of the sphere to the surface) is $4.8 \, cm.$

Substitute the value of the radius into the formula for the surface area of a sphere:

\text{SA }=4 \times \pi \times 4.8^2

3Complete the calculation.

Use a calculator to find the value for the surface area:

\begin{aligned}\text{SA }&=4 \times \pi \times 4.8^2 \\\\ &=\cfrac{2304}{25}\pi \\\\ &=289.529179…… \end{aligned}

4Write the final answer, including the units.

Check what form the final answer needs to be. Here you are asked to give the answer to $1$ decimal place.

289.529179… = 289.5 \mathrm{~cm}^2 \, \text{(1dp)}

The surface area of the sphere is $289.5 \mathrm{~cm}^2 \, \text{(1dp)}.$

Example 2: surface area of a sphere

Find the surface area of a sphere with the diameter of $42 \mathrm{~mm}.$

Write your answer to the nearest square millimeter.

Write down the formula.

To answer the question, use the formula for the surface area of a sphere:

$\text{Surface area}=4 \pi r^2$

Substitute the given values into the formula.

Because the diameter is twice the length of the radius, divide the diameter by $2$ to get the value for $r \text{:}$

$\begin{aligned}r&=d\div{2} \\\\ &=42\div{2} \\\\ &=21\end{aligned}$

So the radius $r=21 \, mm.$ Now, substitute $r=21$ into the formula for the surface area of a sphere to get:

$\text{SA }=4 \times \pi \times 21^2$

Complete the calculation.

Use a calculator to work out the value.

$\begin{aligned}\text{SA }&=4 \times \pi \times 21^2 \\\\ &=1764\pi \\\\ &=5541.769441… \end{aligned}$

Write the final answer, including the units.

Here you are asked to write the answer to the nearest square millimeter and so:

$5541.769441… = 5542 \, \text{mm}^2 \, \text{(0dp)}$

The surface area of the sphere is $5542 \mathrm{~mm}^2 \, \text{(0dp)}.$

Example 3: surface area of a sphere – in terms of π

Find the surface area of a sphere with a radius of $6 \, m.$

Leave your answer in terms of $\pi.$

Write down the formula.

To answer the question, use the formula for the surface area of a sphere:

$\text{Surface area}=4 \pi r^2$

Substitute the given values into the formula.

Substitute the value of the radius into the surface area of a sphere formula.

$\text{SA }=4 \times \pi \times 6^2$

Complete the calculation.

Work out the curved surface area, focussing on the number parts of the calculation.

\begin{aligned}\text{SA }&=4 \times \pi \times 6^2 \\\\ &=144\pi \end{aligned}

Write the final answer, including the units.

Here you are asked to give the answer in terms of $\pi.$

$144\pi\text{ m}^2$

The surface area of the sphere is $144\pi\text{ m}^2.$

Example 4: surface area of a sphere

Find the surface area of the sphere below. Write your answer to $2$ decimal places.

Write down the formula.

To answer the question, use the formula for the surface area of a sphere:

$\text{Surface area}=4 \pi r^2$

Substitute the given values into the formula.

The radius (the distance from the center of the sphere to the surface) is $12.4 \, cm.$

Substitute the value of the radius into the formula for the surface area of a sphere:

$\text{SA }=4 \times \pi \times 12.4^2$

Complete the calculation.

Use a calculator to find the value for the surface area:

$\begin{aligned}\text{SA }&=4 \times \pi \times 12.4^2 \\\\ & =615.04 \pi \\\\ & =1932.20515 \ldots\end{aligned}$

Write the final answer, including the units.

Check what form the final answer needs to be. Here you are asked to give the answer to $2$ decimal places.

$1932.20515 . \ldots=1932.21 \mathrm{~cm}^2 \, \text{(2dp)}$

The surface area of the sphere is $1932.21 \mathrm{~cm}^2 \, \text{(2dp)}.$

Example 5:

The surface area of a sphere is $600 \mathrm{~cm}^2.$ Calculate the radius of the sphere. Write your answer to $1$ decimal place.

Write down the formula.

To answer the question, use the formula for the surface area of a sphere:

$\text{Surface area}=4 \pi r^2$

Substitute the given values into the formula.

The surface area is given, so substitute this into the formula.

$600=4 \pi r^2$

Complete the calculation.

Rearrange the formula to find the value of $r.$

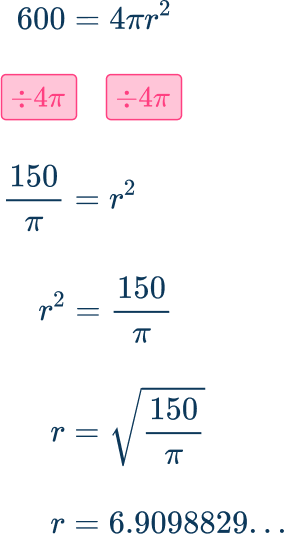
Write the final answer, including the units.

r=6.9098829 \ldots=6.9 \mathrm{~cm} \, \text{(1dp)}

The radius of the sphere is $6.9 \mathrm{~cm} \, \text{(1dp)}.$

Example 6:

The surface area of a sphere is $4000 \mathrm{~cm}^2.$ Calculate the radius of the sphere. Write your answer to $1$ decimal place.

Write down the formula.

To answer the question, use the formula for the surface area of a sphere:

$\text{Surface area}=4 \pi r^2$

Substitute the given values into the formula.

The surface area is given, so substitute this into the formula.

$4000=4 \pi r^2$

Complete the calculation.

Rearrange the formula to find the value of $r.$

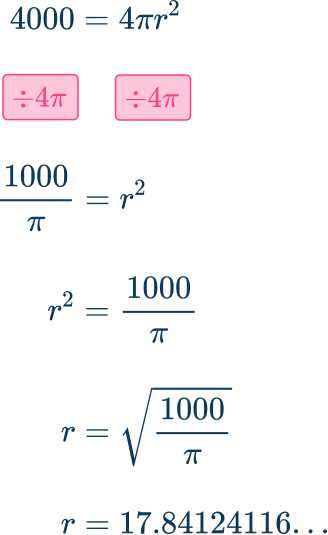
Write the final answer, including the units.

r=17.84124116…=17.8 \mathrm{~cm} \, \text{(1dp)}

The radius of the sphere is $17.8 \mathrm{~cm} \, \text{(1dp)}$ .

Teaching tips for surface area of a sphere

Use visuals, such as diagrams and real life examples, to help students visualize what the shape of a sphere looks like and what it means to calculate the surface area.

Provide practice problems at various difficulty levels for students to work through. This can be done with worksheets, or with interactive technology. Allow students to work together and independently to reinforce understanding.

Have students find the surface area of multiple shapes and compare them. This will better help students understand the formulas they use, and why certain shapes are used in different real life situations.

Easy mistakes to make

Rounding too soon
It is important to not round the answer until the end of the calculation. This will mean your final answer is accurate.

Not using the correct units
For area, use square units such as $\mathrm{~cm}^2.$
For volume, use cube units such as $\mathrm{~cm}^3.$

Incorrectly using the radius or the diameter
It is a common error to mix up radius and diameter. Remember the radius is half of the diameter.

Confusing the volume formula with the surface area formula
It is a common error to mix up the formula for the volume of a sphere with the formula for the surface area of a sphere.
Remember that the surface area formula includes a squared term, whereas the volume formula includes a cubed term.

Practice surface area of a sphere questions

314.2 \mathrm{~cm}^2

942.5 \mathrm{~cm}^2

1256.6 \mathrm{~cm}^2

4188.8 \mathrm{~cm}^2

You are finding the surface area of a sphere, so substitute the value of $r$ into the formula.

\begin{aligned}\text{Surface area}&=4\pi r^2 \\\\ &=4 \times \pi \times 10^2 \\\\ &=400\pi \\\\ &=1256.637061… \\\\ &=1256.6 \text{ cm}^2 \text{ (1dp)} \end{aligned}

32.2 \mathrm{~cm}^2

128.7 \mathrm{~cm}^2

137.3 \mathrm{~cm}^2

514.7 \mathrm{~cm}^2

To find the surface area of a sphere, substitute the value of $r$ into the formula. The diameter is given, so half $6.4$ to get the radius, then substitute this value into the formula for the surface area of a sphere.

r=d\div{2}=6.4\div{2}=3.2\text{ cm}.

\begin{aligned}\text{Surface area}&=4\pi r^2 \\\\ &=4 \times \pi \times 3.2^2 \\\\ &=\cfrac{1024}{25}\pi \\\\ &=128.679351… \\\\ &=128.7 \text{ cm}^2 \text{ (1dp)} \end{aligned}

324\pi\text{ m}^2

36\pi\text{ m}^2

81\pi\text{ m}^2

972\pi\text{ m}^2

To find the surface area of a sphere, substitute the value of $r$ into the formula.

\begin{aligned}\text{Surface area}&=4\pi r^2 \\\\ &=4 \times \pi \times 9^2 \\\\ &=324\pi \\\\ &=324\pi \text{ m}^2 \end{aligned}

1520.53 \mathrm{~cm}^2

44 \mathrm{~cm}^2

484 \mathrm{~cm}^2

2520.53 \mathrm{~cm}^2

To find the surface area of a sphere, substitute the value of $r$ into the formula.

\begin{aligned}& =4 \times \pi \times 11^2 \\\\ & =484 \pi=1520.530844 \ldots \\\\ & =1520.53 \mathrm{~cm}^2 \end{aligned}

26.7 \mathrm{~cm}

26.8 \mathrm{~cm}

53.5 \mathrm{~cm}

53.6 \mathrm{~cm}

Using the formula, we substitute the value of the surface area and rearrange to find the radius.

\begin{aligned}\text{SA }&=4 \pi r^2 \\\\ 9000 &= 4\pi r^2 \\\\ 2250 &= \pi r^2 \\\\ \cfrac{2250}{\pi}&=r^2 \\\\ r&=\sqrt{\cfrac{2250}{\pi}} \\\\ r&=26.76186174… \\\\ r&=26.8 \text{ cm (3sf)} \end{aligned}

\$ 87

\$ 65

\$ 78

\$ 93

To find the surface area of a sphere, substitute the value of $r,$ the radius of the ball, into the formula.

4 \times \pi \times 30^2=3600\pi=11309.73355…

Next, divide the surface area by the number of square inches that a tin of paint covers.

11309.73355 \div {2000} = 5.654866776… = 6 \text{ tins}

Multiply the number of tins needed by the total cost of each tin of paint.

6 \times 13=\$ 78

Surface area of a sphere FAQS

What is a sphere?

A sphere is a three-dimensional shape that is perfectly round. It can be defined as the set of all points in three dimensional space that are a fixed distance (radius) from a given point (the center).

How do you calculate the diameter of the sphere?

The diameter of a sphere is twice the length of its radius. If you are given the radius of the sphere, simply double it to find the diameter. Alternatively, if you are given the diameter and need the radius, you can divide the diameter by $2$ to find the radius.

What is the difference between a sphere and a circle?

A circle is a two-dimensional shape with a flat surface. A sphere is a three dimensional shape that is perfectly round, like a ball. The circle can also be thought of as the cross section of a sphere.

Did you know?

Archimedes was a famous ancient Greek mathematician who lived about $2,200$ years ago in Sicily. He wrote about the surface area of a sphere and said it was four times the area of the greatest circle. This is the same formula that is used today.

Archimedes also worked on cylinders and discovered the formula for the lateral surface area of a cylinder. The lateral surface area excludes its circular base and top. This is usually referred to as its curved surface area.

The next lessons are

Pythagorean Theorem
Congruence and similarity
Transformations

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.