High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Area of a rectangle Area of a triangle 3D shapes Math netsSurface area of a triangular prism
Here you will learn about the surface area of a triangular prism, including what it is and how to calculate it.
Students will first learn about the surface area of a triangular prism as part of geometry in 6th grade.
What is the surface area of a triangular prism?
The surface area of a triangular prism is the total area of all of the faces of the triangular prism.
To calculate the surface area of triangular prisms, you need to calculate the area of each face and add them all together.
A triangular prism has two triangular bases, and the lateral faces are the three rectangular faces. The lateral surface area of a triangular prism is the total area of the rectangular sides.
The triangular faces of a triangular prism are congruent (exactly the same), but unless the triangle is isosceles or equilateral, the rectangles will be all different.
For example,
You can also use the net of a triangular prism to find the area. The triangular prism above unfolded into its net would be:
Since it is an area, surface area is measured in square units (e.g. mm^2, \, cm^2, \, m^2 etc).
What is the surface area of a triangular prism?
![[FREE] Surface Area of a Triangular Prism Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Surface-Area-of-a-Triangular-Prism-Worksheet-listing-image.png)
[FREE] Surface Area of a Triangular Prism Worksheet (Grade 6 to 8)
Use this worksheet to check your grade 6 to 8 students’ understanding of the surface area of a triangular prism. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE [FREE] Surface Area of a Triangular Prism Worksheet (Grade 6 to 8)
Use this worksheet to check your grade 6 to 8 students’ understanding of the surface area of a triangular prism. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this relate to 6th grade math?
- Grade 6 – Geometry (6.G.A.4)
Represent three-dimensional figures using nets made up of rectangles and triangles, and use the nets to find the surface area of these figures. Apply these techniques in the context of solving real-world and mathematical problems.
How to calculate the surface area of a triangular prism
In order to calculate the surface area of a triangular prism:
- Calculate the area of each face.
- Add the five areas together.
- Include the units.
Surface area of a triangular prism examples
Example 1: how to find the surface area of a right triangular prism
Calculate the surface area of the triangular prism.
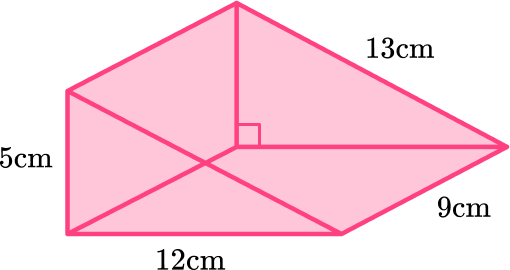
- Calculate the area of each face.
The area of the triangle at the front is \cfrac{1}{2} \times 12 \times 5=30 \mathrm{~cm}^2 .
The back face is the same as the front face so the area of the back is also 30 \, cm^2.
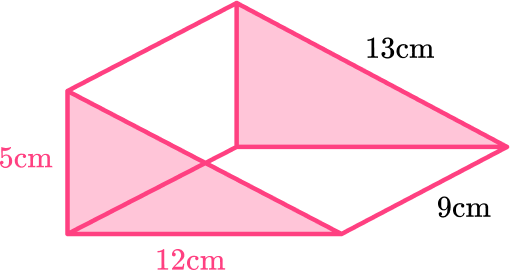
The area of the base is 9 \times 12=108 \mathrm{~cm}^2 .
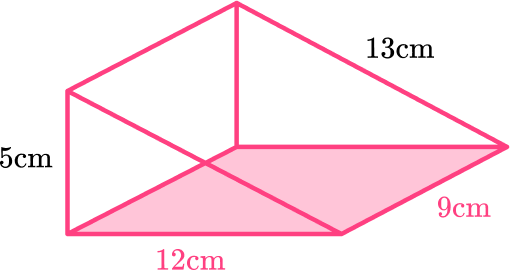
The area of the left side is 9 \times 5=45 \mathrm{~cm}^2 .
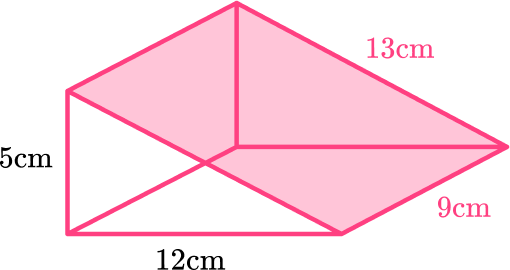
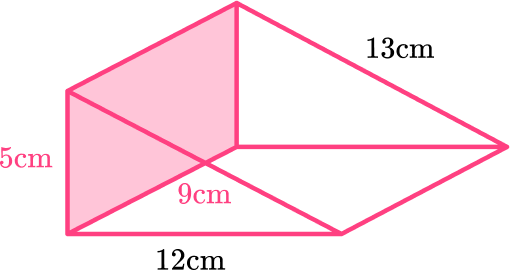
The area of the top is 9 \times 13=117 \mathrm{~cm}^2 .
If you have trouble keeping track of all the calculations, use a table:
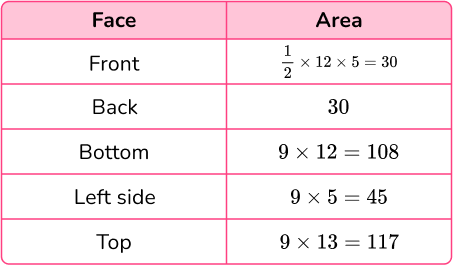
2Add the five areas together.
Total surface area: 30+30+108+45+117 = 330
3Include the units.
The measurements on the triangular prism are in cm therefore, the total surface area of the triangular prism is 330 \mathrm{~cm}^2.
Example 2: surface area of a triangular prism with an isosceles triangle
Calculate the surface area of the triangular prism.
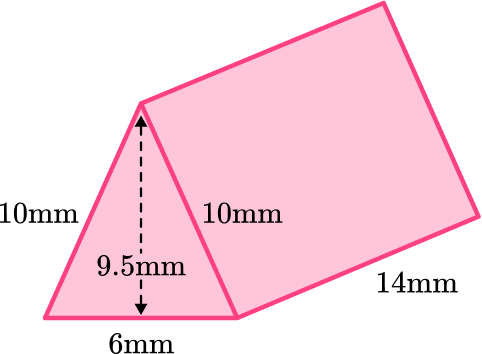
Calculate the area of each face.
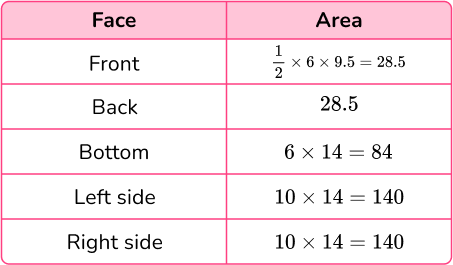
Add the five areas together.
Total surface area: 28.5+28.5+84+140+140 = 421
Include the units.
The measurements on the triangular prism are in mm , therefore the total surface area of the triangular prism is 421 \mathrm{~mm}^2.
Example 3: surface area of a right triangular prism
Calculate the surface area of the triangular prism.
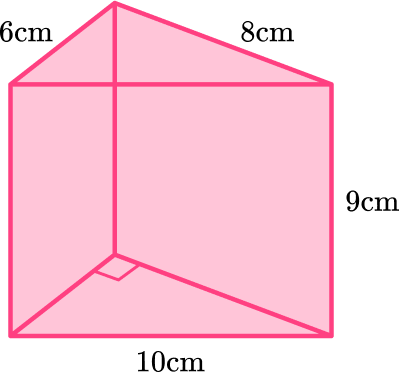
Calculate the area of each face.
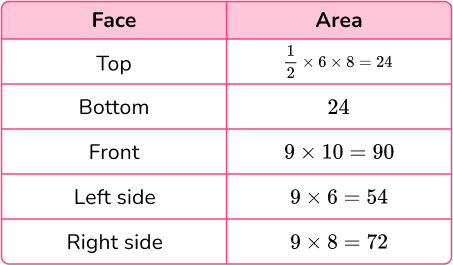
Add the five areas together.
Total surface area: 24+24+90+54+72 = 264
Include the units.
The measurements on the triangular prism are in cm , therefore the total surface area of the triangular prism is 264 \mathrm{~cm}^2.
Example 4: surface area of a triangular prism
Calculate the surface area of the triangular prism.
Calculate the area of each face.
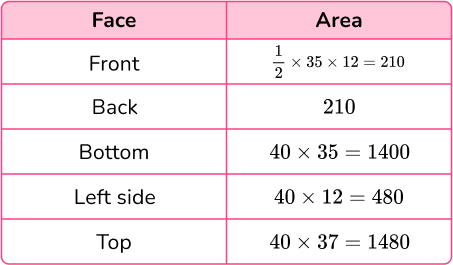
Add the five areas together.
Total surface area: 210+210+1,400+480+1,480=3,780
Include the units.
The measurements on the triangular prism are in m, therefore the total surface area of the triangular prism is 3,780 \mathrm{~m}^2.
Example 5: surface area of a triangular prism with different units
Calculate the surface area of the triangular prism. Give your answer in mm^2.
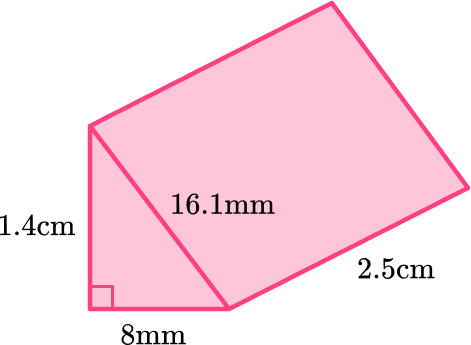
Calculate the area of each face.
Some of the measurements here are in cm and some are in mm. Since you have been asked for the answer in \mathrm{mm}^2, you need to convert all measurements to mm.
1.4 \mathrm{~cm}=14 \mathrm{~mm} and 2.5 \mathrm{~cm}=25 \mathrm{~mm}.
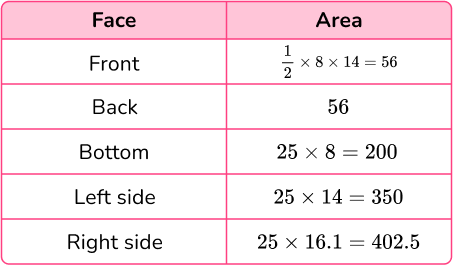
Add the five areas together.
Total surface area: 56+56+200+350+402.5=1,064.5
Include the units.
The measurements you have used are in mm, therefore the total surface area of the triangular prism is 1,064.5 \mathrm{~mm}^2.
Example 6: surface area when there is a missing length
Calculate the surface area of the triangular prism. Give your answer in cm^2.
Calculate the area of each face.
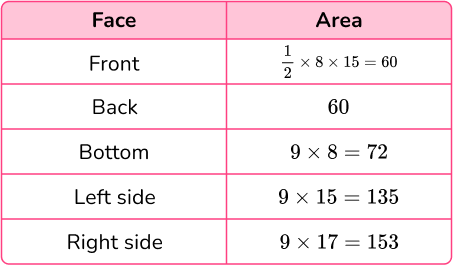
Add the five areas together.
Total surface area: 60+60+72+135+153=480
Include the units.
The measurements you have used are in cm therefore the total surface area of the triangular prism is 480 \mathrm{~cm}^2.
[FREE] Surface Area of a Triangular Prism Worksheet (Grade 6 to 8)
Use this worksheet to check your grade 6 to 8 students’ understanding of the surface area of a triangular prism. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE [FREE] Surface Area of a Triangular Prism Worksheet (Grade 6 to 8)
Use this worksheet to check your grade 6 to 8 students’ understanding of the surface area of a triangular prism. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREETeaching tips for the surface area of a triangular prism
- Give students access to physical models of triangular prisms and their nets before introducing this skill. Calculating the surface area of any 3D shape requires students to be able to think spatially about the shape.
Particularly when students have to use a 2D representation of a 3D shape to solve (like the images in worksheets or websites, including the ones on this page). This is much easier for students to do if they have done adequate work with real life triangular prisms.
- Start with activities that show the nets of triangular prisms on square grids. This helps students understand why surface area is measured in square units. It also provides visual support for students who are not as comfortable with using the area formulas or don’t have a full conceptual understanding of what area is.
- Always look for worksheets that include a variety of triangular bases, not just one type.
Easy mistakes to make
- Calculating volume instead of surface area
Volume and surface area are different things – volume tells us the space within the shape whereas surface area is the total area of the faces. To find surface area, calculate the area of each face and add them together.
- Thinking all of the rectangles have the same area
Each of the rectangles may have different areas (unless the triangle is isosceles or equilateral).
For example,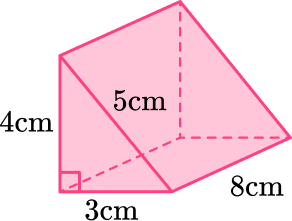
unfolds to be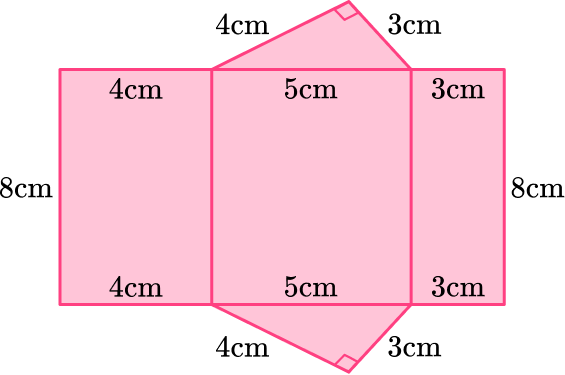 
Both the prism and its net show the rectangles:
∘ 8 \, cm \times 4 \, cm
∘ 8 \, cm \times 5 \, cm
∘ 8 \, cm \times 3 \, cm
- Using the wrong measurements to calculate the area of the triangle faces
In surface area questions, you need to know the length of all three sides of the triangle however, you only need the base and the height to calculate the area of the triangle.
Practice surface area of a triangular prism questions
1. Calculate the surface area of the right triangular prism.
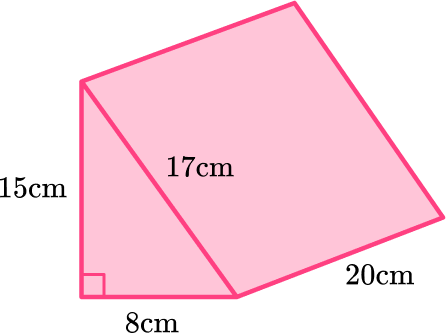
Calculate the surface area of each face:
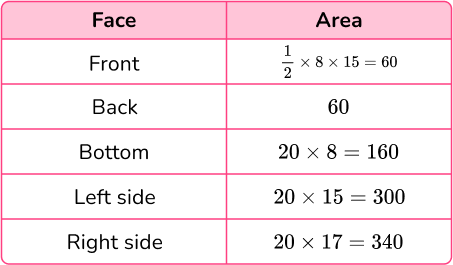
Total surface area =60+60+160+300+340=920\mathrm{~cm}^{2}
2. Calculate the surface area of the triangular prism.
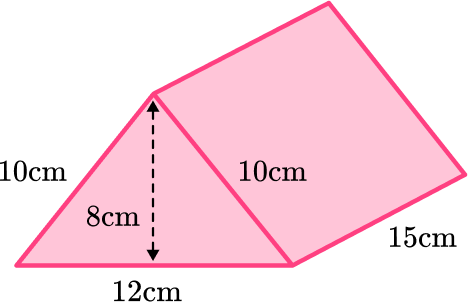
Calculate the surface area of each face:
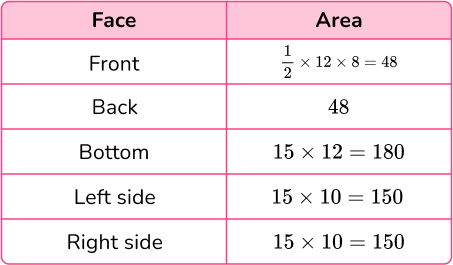
Total surface area =48+48+180+150+150=576\mathrm{~cm}^{2}
3. Calculate the surface area of the triangular prism.
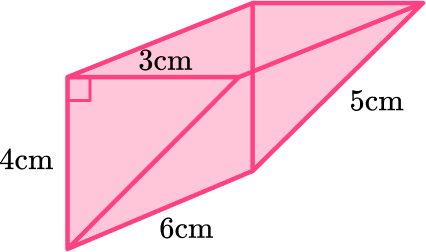
Calculate the surface area of each face:
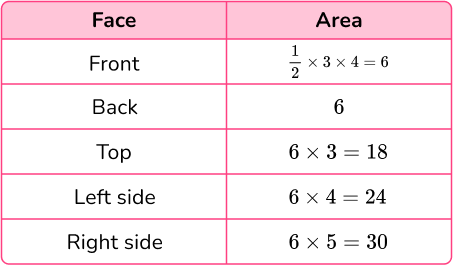
Total surface area =6+6+18+24+30=84\mathrm{~cm}^{2}
4. Calculate the surface area of the triangular prism.
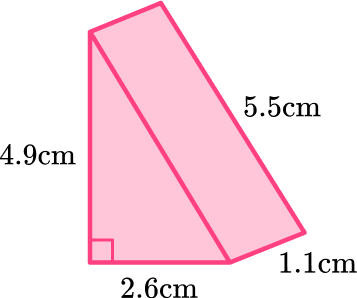
Calculate the surface area of each face:
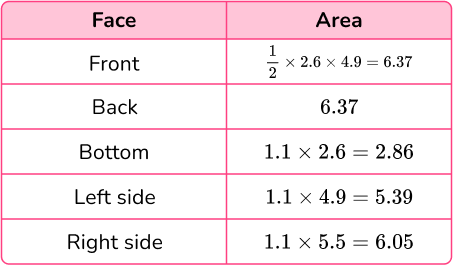
Total surface area =6.37+6.37+2.86+5.39+6.05=27.04\mathrm{cm}^{2}
5. Calculate the surface area of the triangular prism. Give your answer in square centimeters.
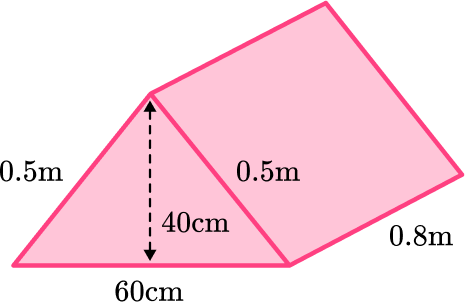
Notice that some of the measurements are in m and some are in cm.
Since you are asked to give the answer in square centimeters, you need to convert all the measurements to cm.
0.5 \mathrm{~m}=50 \mathrm{~cm} and 0.8 \mathrm{~m}=80 \mathrm{~cm}
Next, calculate the surface area of each face:
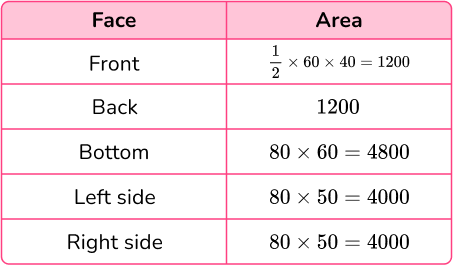
Total surface area =1200+1200+4800+4000+4000=15200 \mathrm{~cm}^{2}
6. Calculate the surface area of the triangular prism
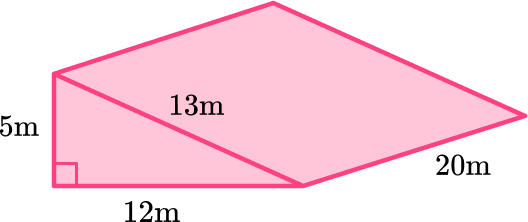
Calculate the surface area of each face:
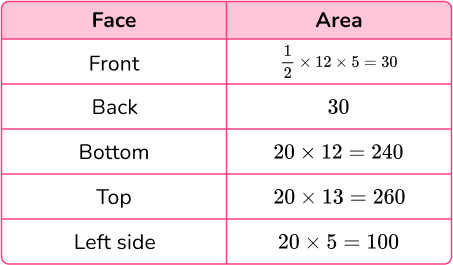
Total surface area =30+30+240+260+100=660 \mathrm{~m}^{2}
Surface area of a triangular prism FAQs
Regardless of how the prism is oriented, the height is always the distance between the bases, or the height of the 3 rectangles that form the lateral faces.
Yes, in general terms, the surface area is equal to the perimeter of the base times the length of the prism, plus the area of the base doubled. This can also be written as the formula:
(S1 +S + S3)L + bh.
Note, however, that students are usually not expected to memorize this formula. Since a triangular prism has 5 faces with varying dimensions, it is usually easier for students to remember to find the area of the bases and the three rectangular faces and then add them all together.
This would only be necessary if the base were a right triangle and one of the lengths was missing. However, following the Common Core State Standards, students learn how to calculate surface area before working with the Pythagorean theorem, so avoid these types of problems until students have learned this topic.
The next lessons are
- Pythagorean theorem
- Trigonometry
- Circle math
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!