Surface Area of a Hemisphere - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Multiplying fractions Area of a circle Rounding Surface area of a sphere Volume of a sphere Square roots

Math resources Geometry Surface area

Surface area of a hemisphere

Here you will learn about the surface area of a hemisphere, including how to find the curved surface area of a hemisphere and the total surface area of a hemisphere.

Students will first learn about the surface area of a hemisphere as part of geometry in $8$ th grade.

What is the surface area of a hemisphere?

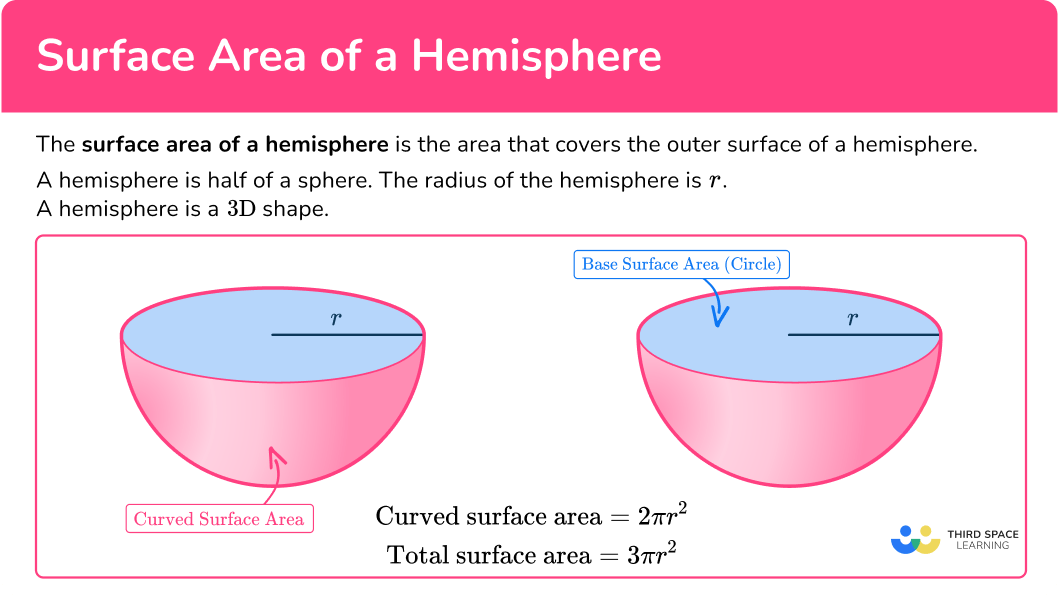
The surface area of a hemisphere is the area that covers the outer surface of a hemisphere.

To calculate the surface area of a hemisphere, you need to know what a hemisphere is. A hemisphere is a 3D shape that is half of a sphere. It has a curved surface and a circular base, which is a flat surface. The radius of the hemisphere is $r.$

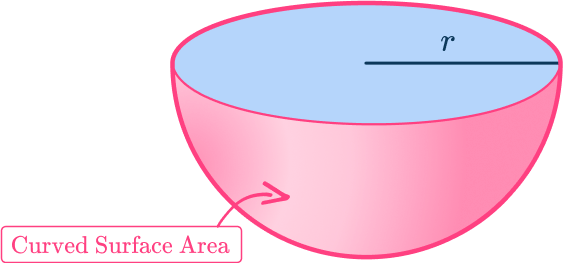
To calculate the surface area of a sphere with radius $r,$ you can use the formula

$\text{SA}=4\pi{r}^{2}$

You can then adapt this formula for a hemisphere. To find the curved surface area of the hemisphere you need to halve the surface area of the sphere.

$4\pi{r}^{2}\div{2}=2\pi{r}^{2}$

This would only give the curved surface area of the hemisphere.

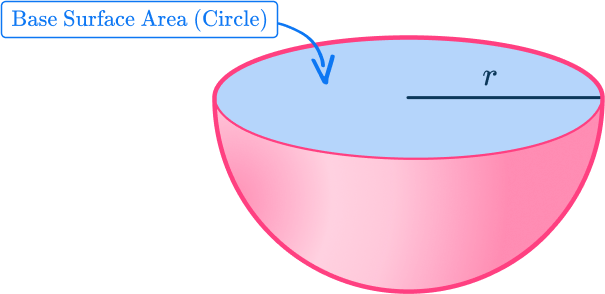
In order to calculate the total surface area, you need to add the curved surface area to the area of the base of the hemisphere. The base surface is a circle, and to calculate the area of the circle, you need to use the formula $A=\pi{r^2}.$

Therefore, the total surface area of a hemisphere formula is:

$\text{Total Surface Area}=2\pi{r}^{2}+\pi{r}^{2}=3\pi{r}^{2}$

What is the surface area of a hemisphere?

Common Core State Standards

How does this relate to $8$ th grade math?

Grade 8 – Geometry (8.G.C.9)
Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.

[FREE] Surface Area Worksheet (Grade 6)

Use this quiz to check your grade 6 students’ understanding of surface area. 10+ questions with answers covering a range of 6th grade surface area topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Surface Area Worksheet (Grade 6)

Use this quiz to check your grade 6 students’ understanding of surface area. 10+ questions with answers covering a range of 6th grade surface area topics to identify areas of strength and support!

DOWNLOAD FREE

How to calculate the surface area of a hemisphere

In order to calculate the surface area of a hemisphere:

Find the curved surface area of the hemisphere.
Find the base surface of the hemisphere.
Determine the solution.

Surface area of a hemisphere examples

Example 1: curved surface area, radius of a hemisphere is given

Calculate the curved surface area of a hemisphere with radius $12\mathrm{~cm}.$ Give your answer to the nearest tenth.

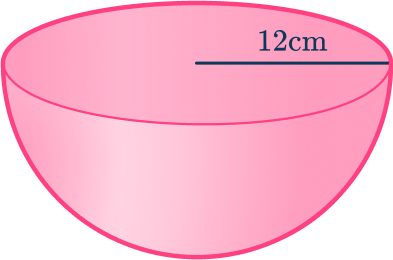
Find the curved surface area of the hemisphere.

You can halve the surface area of a sphere $(\text{SA}=4\pi{r^2})$ to find the curved surface area of the hemisphere.

4\pi{r^2}\div{2}=2\pi{r}^{2}

Substitute the value of the radius $r=12.$

2\pi{r^2}=2\pi{12}^{2}=2\pi\times{144}=904.7786…

2Find the base surface of the hemisphere.

The base surface area is not needed for this example.

3Determine the solution.

The curved surface area is $904.8\mathrm{~cm}^2$ to the nearest tenth.

Example 2: total surface area, radius given

Calculate the total surface area of a hemisphere with radius $8.5\mathrm{~m}.$ Give your answer to the nearest tenth.

Find the curved surface area of the hemisphere.

You can halve the surface area of a sphere $(\text{SA}=4\pi{r^2})$ to find the curved surface area of the hemisphere.

$4\pi{r^2}\div{2}=2\pi{r}^{2}$

Substitute the value of the radius $r=8.5.$

$2\pi{r^2}=2\pi({8.5})^{2}=2\pi\times{72.25}=453.9601…$

Find the base surface of the hemisphere.

The base area is a circle. The area of a circle is $A=\pi{r^2}.$ Here, the radius $r=8.5.$

$\pi{r^2}=\pi(8.5)^{2}=\pi\times{72.25}=226.9800…$

Determine the solution.

453.9601\dots+226.9800\dots=680.9402\dots

This rounds to give the total surface area $680.9\mathrm{~m}^2$ to the nearest tenth.

Example 3: total surface area, diameter given

Calculate the total surface area of a hemisphere with diameter $6.8\mathrm{~cm}.$ Give your answer to the nearest tenth.

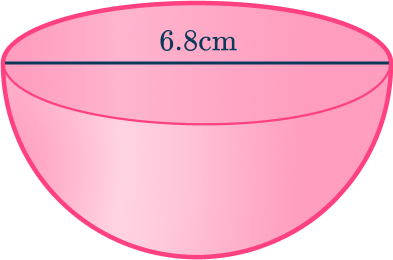
Find the curved surface area of the hemisphere.

You can halve the surface area of a sphere $(\text{SA}=4\pi{r^2})$ to find the curved surface area of the hemisphere.

$4\pi{r^2}\div{2}=2\pi{r}^{2}$

Halve the diameter $d=6.8\mathrm{~cm}$ to get the radius, $r.$

$d\div{2}=6.8\div{2}=3.4\mathrm{~cm}$

Substitute the value of the radius $r=3.4.$

$2\pi{r^2}=2\pi({3.4})^{2}=2\pi\times{11.56}=72.6336…$

Find the base surface of the hemisphere.

The base area is a circle. The area of a circle is $A=\pi{r^2}.$ Here, the radius $r=3.4.$

$\pi{r^2}=\pi(3.4)^{2}=\pi\times{11.56}=36.3168…$

Determine the solution.

72.6336\dots+36.3168\dots=108.9504\dots

This rounds to give the total surface area $109.0\mathrm{~cm}^2$ to the nearest tenth.

Example 4: curved surface area, radius given, leave answer in terms of π

A glass marble is cut directly in half to create a hemisphere. Calculate the curved surface area of the marble with radius $7\mathrm{~mm}.$ Leave your answer in terms of $\pi.$

Find the curved surface area of the hemisphere.

You can halve the surface area of a sphere $(\text{SA}=4\pi{r^2})$ to find the curved surface area of the hemisphere.

$4\pi{r^2}\div{2}=2\pi{r}^{2}$

Substitute the value of the radius $r=7.$

$2\pi{r^2}=2\pi({7})^{2}=2\pi\times{49}=98\pi$

Find the base surface of the hemisphere.

The question only requires the curved surface area.

Determine the solution.

The curved surface area is $98\pi\mathrm{~mm}^2$ in terms of $\pi.$

Example 5: total surface area, radius of a hemisphere is given, leave answer in terms of π

A polystyrene ball is cut in half to get a hemisphere with a radius of $9\mathrm{~cm}.$ Calculate the total surface area of a hemisphere. Leave your answer in terms of $\pi.$

Find the curved surface area of the hemisphere.

You can halve the surface area of a sphere $(\text{SA}=4\pi{r^2})$ to find the curved surface area of the hemisphere.

$4\pi{r^2}\div{2}=2\pi{r}^{2}$

Substitute the value of the radius $r=9.$

$2\pi{r^2}=2\pi({9})^{2}=2\pi\times{81}=162\pi$

Find the base surface of the hemisphere.

The base area is a circle. The area of a circle is $A=\pi{r^2}.$ Here, the radius $r=9.$

$\pi{r^2}=\pi(9)^{2}=\pi\times{81}=81\pi$

Determine the solution.

162\pi+81\pi=243\pi\mathrm{~cm}^2

How to calculate the radius of a hemisphere, given the surface area

In order to calculate the radius of a hemisphere when given the surface area:

Determine which surface area formula to use.
Substitute known values into the formula.
Solve for the radius, $\textbf{r}.$

Example 6: finding the radius of a hemisphere, given the total surface area

The total surface area of a hemisphere is $300\mathrm{~cm}^2.$ Calculate the radius of the hemisphere. Give your answer to the nearest hundredth.

Determine which surface area formula to use.

Here, the total surface area has been given, so use the formula:

$\text{Total surface area}=3\pi{r^2}$

Substitute known values into the formula.

The question states that the total surface area is $300\mathrm{~cm}^2,$ so:

$3\pi{r^2}=300$

Solve for the radius, $\textbf{r}.$

\begin{aligned}3\pi{r^2}\div{3}\pi&=300\div{3}\pi \\\\ r^2&=\cfrac{300}{3\pi} \\\\ r^{2}&=\cfrac{100}{\pi} \\\\ r&=\sqrt{\cfrac{100}{\pi}} \\\\ r&=5.64\mathrm{~cm}\text{ (nearest hundredth)} \end{aligned}

Example 7: finding the diameter of a hemisphere, given the curved surface area

The Panthéon in Rome has a famous hemispherical dome roof. The curved surface area is $10082\pi\mathrm{~ft}^2.$ Calculate the diameter of the dome in feet.

Determine which surface area formula to use.

Here, the curved surface area has been given, so use the formula

$\text{Curved surface area}=2\pi{r^2}$

Substitute known values into the formula.

The question states that the curved surface area is $10082\pi\mathrm{~ft}^2$ , so

$2\pi{r^2}=10082\pi$

Solve for the radius, $\textbf{r}.$

\begin{aligned}2\pi{r^2}\div{2}\pi&=10082\pi\div{2}\pi \\\\ r^2&=5041 \\\\ r&=\sqrt{5041} \\\\ r&=71\mathrm{~ft} \end{aligned}

The diameter is double the radius. The diameter of the dome roof is

$d=71\times{2}=142\mathrm{~ft}$

Teaching tips for surface area of a hemisphere

Bring a physical model of a hemisphere, like a dome-shaped object or a model of earth split into hemispheres, to the class. Allow students to hold and examine it.

Show students real life examples of when they would need to find the total surface area of a hemisphere (solid hemispheres like an orange cut in half) or if they would only need to find the curved surface area of the hemisphere (hollow hemispheres with no base like the shell of a coconut split in half.)

Note that sometimes they may need to find the total surface area of a hollow hemisphere, which would have a curved surface and a circular base but no volume. Some hollow hemispheres may also have an inner radius and outer radius.

Giving students a worksheet or other study materials with solved examples can help reinforce their understanding of how to find the surface area of a hemisphere by demonstrating step-by-step solutions, clarifying formulas, allowing error correction, building confidence, and providing practice.

Easy mistakes to make

Using the incorrect formula
There are several formulas that can be used in geometry, so you need to match the correct formula to the correct context.

Confusing the total surface area and curved surface area
Double check whether the question requires you to find the curved surface area $(csa)$ of the hemisphere or the total surface area $(tsa)$ of the hemisphere.

Rounding too soon
It is important not to round the answer until the end of the calculation. This will mean your final answer is accurate. It is useful to keep your answer in terms of $\pi$ until you round the answer at the very end of the question.

Using the incorrect units
For area, use square units such as $\mathrm{~cm}^2$
For volume, use cube units such as $\mathrm{~cm}^3$

Mixing up the radius with the diameter
It is a common error to mix up radius and diameter. Remember the radius is half of the diameter.

Practice surface area of a hemisphere questions

588.3\mathrm{~cm}^2

344.1\mathrm{~cm}^2

588.2\mathrm{~cm}^2

392.2\mathrm{~cm}^2

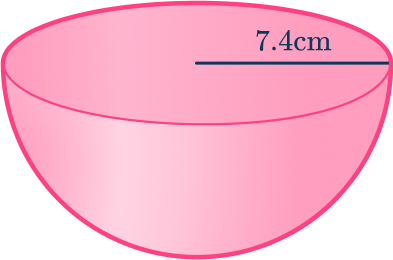
The curved surface area of the hemisphere can be found by halving the surface area of a sphere.

\begin{aligned} \text{Curved surface area}&=4\pi{r^2}\div 2=2\pi{r^2} \\\\ &=2\pi(7.4)^2\ \\\\ &=344.067… \\\\ &=344.1\mathrm{~cm}^2 \\ & \; \text{ (nearest tenth)} \end{aligned}

401.1\mathrm{~km}^2

802.3\mathrm{~km}^2

1203.4\mathrm{~km}^2

3209.2\mathrm{~km}^2

The curved surface area of the hemisphere can be found by halving the surface area of a sphere. You need to add the area of the flat circle as you need the total surface area.

\begin{aligned}\text{Total surface area}&=4\pi{r^2}\div{2}+\pi{r^2} \\\\ &=3\pi{r^2} \\\\\ &=3\pi(11.3)^2 \\\\\ &=1203.449… \\\\\ &=1203.4\mathrm{~cm}^2 \\ & \; \text{ (nearest tenth)} \end{aligned}

588.3\mathrm{~m}^2

1470.8\mathrm{~m}^2

2206.2\mathrm{~m}^2

551.6\mathrm{~m}^2

The total surface area of the hemisphere can be found by halving the surface area of a sphere then adding the area of the base surface (a circle). First you need to divide the diameter by $2$ to find the radius.

r=15.3\div{2}=7.65

\begin{aligned}\text{Total surface area}&=4\pi{r^2}\div{2}+\pi{r^2} \\\\ &=3\pi{r^2} \\\\ &=3\pi(7.65)^2 \\\\ &=551.561… \\\\ &=551.6\mathrm{~m}^2 \\ & \; \text{ (nearest tenth)} \end{aligned}

25\pi\mathrm{~cm}^2

50\pi\mathrm{~cm}^2

75\pi\mathrm{~cm}^2

100\pi\mathrm{~cm}^2

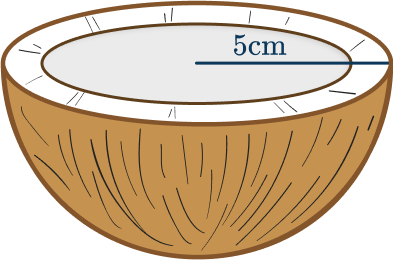
The curved surface area of the coconut can be found by using the surface area of a sphere and halving it.

\begin{aligned}\text{Curved surface area}&=4\pi{r^2}\div{2} \\\\ &=2\pi{r^2} \\\\ &=2\pi(5)^2 \\\\ &=2\pi\times{25} \\\\ &=50\pi\mathrm{~cm}^2 \end{aligned}

363\pi\mathrm{~cm}^2

121\pi\mathrm{~cm}^2

242\pi\mathrm{~cm}^2

484\pi\mathrm{~cm}^2

The curved surface area of the hemisphere can be found by using the surface area of a sphere and halving it. You need to add the area of the base surface (a circle) as you need the total surface area.

\begin{aligned}\text{Total surface area}&=4\pi{r^2}\div{2}+\pi{r^2} \\\\ &=3\pi{r^2} \\\\ &=3\pi(11)^2 \\\\ &=363\pi \\\\ &=363\pi\mathrm{~cm}^2 \end{aligned}

48.9\mathrm{~cm}

28.2\mathrm{~cm}

69.1\mathrm{~cm}

24.4\mathrm{~cm}

The total surface area of the hemisphere is $3\pi{r^2}.$ You can form an equation using the given value and rearrange to solve it.

\begin{aligned}\text{Total surface area}&=3\pi{r^2} \\\\ 7500&=3\pi{r^2} \\\\ 2500&=\pi{r^2} \\\\ \cfrac{2500}{\pi}&=r^2 \\\\ r&=\sqrt{\cfrac{2500}{\pi}} \\\\ r&=28.2094… \\\\ r&=28.2\mathrm{~cm} \\ & \; \text{ (nearest tenth)} \end{aligned}

Surface area of a hemisphere FAQs

What is a hemisphere?

A hemisphere is a three-dimensional shape that represents half of a sphere. It has one curved surface and a flat circular base.

How do you find the total surface area of a hemisphere?

To find the total surface area of a hemisphere, you need to find both the curved surface area and the area of the flat circular base. To do so, you can use the formula $tsa=2\pi{r^2}+\pi{r^2}$ or $tsa=3\pi{r^2}$ , where $r$ is the radius of the hemisphere.

How do you find the curved surface area of a hemisphere?

To find the curved surface area of a hemisphere, you use the following formula: $\text {csa of hemisphere}=2\pi{r^2}$ , where $r$ is the radius of the hemisphere.

What is the difference between surface area of a hemisphere and volume of a hemisphere?

The surface area of a hemisphere is the area that covers the outer surface of a hemisphere. The volume of a hemisphere is the amount of space inside a hemisphere.

The next lessons are

Pythagorean theorem
Trigonometry
Circle math

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.