A cube is a three-dimensional figure with six equal square faces and [katex] 8 [/katex] vertices.

Surface Area of a Cube - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Area of a square 2D shapes 3D shapes

Math resources Geometry Surface area

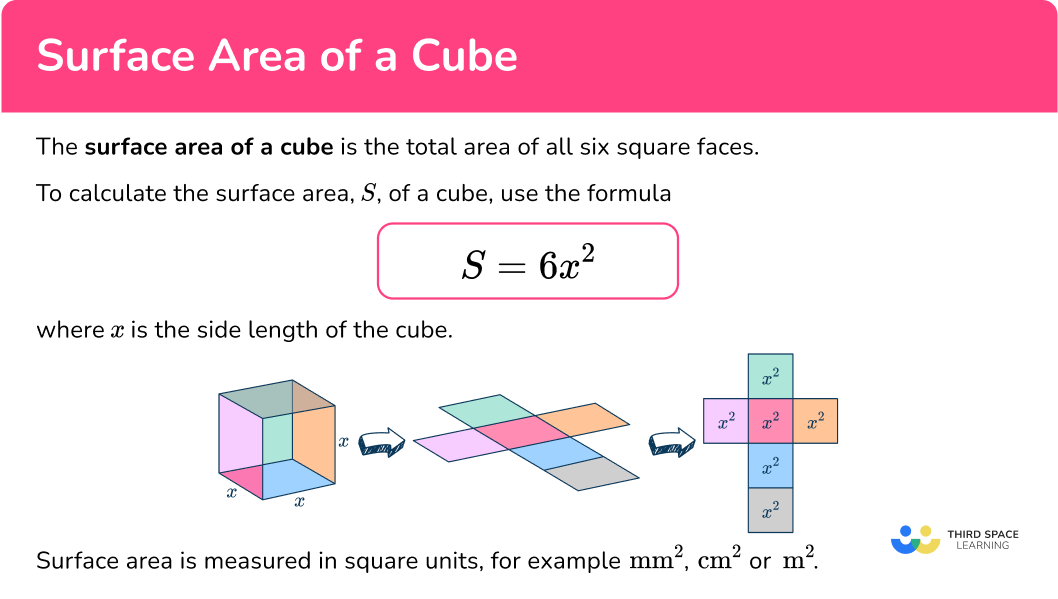
Surface area of a cube

Here you will learn about the surface area of a cube, including how to calculate the surface area of a cube and how to find missing values of a cube given its surface area.

Students will first learn about the surface area of a cube as a part of geometry in $8$ th grade.

What is the surface area of a cube?

The surface area of a cube (cuboid) is the sum of the areas of all the faces of a cube. This is also referred to as the total surface area of a cube (tsa) or the lateral surface area of a cube.

A cube is a three-dimensional figure that has six congruent square faces. This means that all the side faces are the same size.

To find the area of each face, multiply the side lengths together. Then multiply the area of each of the square faces by six.

The formula to calculate the surface area, $S,$ of a cube is $S=6x^{2}$ where $x$ represents the side length (edge length) of the cube.

The surface area of a cube formula can be used to find the surface area of any cube.

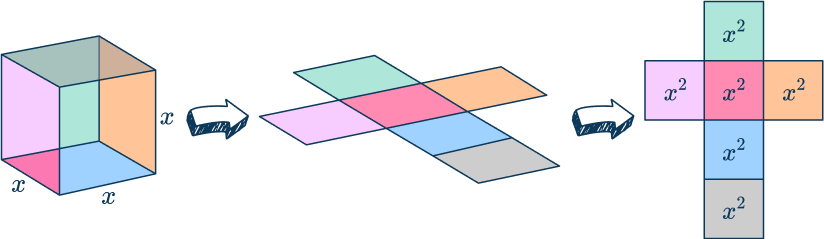
Surface area is measured in square units, for example $mm^{2}, \, cm^{2}$ or $\, m^{2}.$

What is the surface area of a cube?

Common Core State Standards

How does this relate to $8$ th grade math?

Grade 8: Geometry (8.G.C.9)
Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.

[FREE] Surface Area Worksheet (Grade 6)

Use this quiz to check your grade 6 students’ understanding of surface area. 10+ questions with answers covering a range of 6th grade surface area topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Surface Area Worksheet (Grade 6)

Use this quiz to check your grade 6 students’ understanding of surface area. 10+ questions with answers covering a range of 6th grade surface area topics to identify areas of strength and support!

DOWNLOAD FREE

How to calculate the surface area of a cube

In order to calculate the surface area of a cube:

Write the formula for the surface area of the cube.
Substitute any known value(s) into the formula.
Complete the calculation.
Write the solution, including the units.

Surface area of a cube examples

Example 1: surface area of a cube (integer side lengths)

Find the surface area of the cube below.

Write the formula for the surface area of the cube.

S=6x^{2}

2Substitute any known value(s) into the formula.

Here, $x=5$ and so $S=6\times{5}^{2}.$

3Complete the calculation.

S=6\times{5}^{2}=6\times{25}=150

4Write the solution, including the units.

As the unit of length is centimeters $(cm),$ the unit of area is square centimeters $(cm^{2}).$

S=150 \, cm^{2}

Example 2: surface area of a cube (one known edge of the cube)

Find the surface area of the cube.

Write the formula for the surface area of the cube.

S=6x^{2}

Substitute any known value(s) into the formula.

Substituting $x=6$ into the formula, we have $S=6\times{6}^{2}.$

Complete the calculation.

S=6\times{6}^{2}=6\times{36}=216

Write the solution, including the units.

As the unit of length is centimeters $(cm),$ the unit of area is square centimeters $(cm^{2}).$

$S=216 \, cm^{2}$

Example 3: surface area of a cube (worded problem)

A cube structure has a side length of $7 \, m.$ Calculate the total surface area of the structure.

Write the formula for the surface area of the cube.

S=6x^{2}

Substitute any known value(s) into the formula.

Substituting $x=7$ into the formula, $S=6\times{7}^{2}.$

Complete the calculation.

S=6\times{7}^{2}=6\times{49}=294

Write the solution, including the units.

As the unit of length is meters $(m),$ the unit of area is square meters $(m^{2}).$

$S=294 \, m^{2}$

Example 4: surface area of a cube (area of a face given)

The area of the face of a cube is $30 \, cm^{2}.$ Find the surface area of the cube.

Write the formula for the surface area of the cube.

S=6x^{2}

Substitute any known value(s) into the formula.

Knowing the area of one face of the cube, you can express this as $x^2=30$ as $x$ is the side length of the cube, and you know the area, $x^2.$

Substituting $x^2=30$ into the formula, you have $S=6\times{30}.$

Complete the calculation.

S=6\times{30}=180

Write the solution, including the units.

As the unit of area is square centimeters $(cm^{2}),$ you can use this in the solution.

$S=180 \, cm^{2}$

Example 5: find the length of a cube given the surface area

The surface area of a cube is $24 \, ft^{2}.$ Find the length of the cube.

Write the formula for the surface area of the cube.

S=6x^{2}

Substitute any known value(s) into the formula.

Here you know that $S=24$ and so substituting this into the formula,

24=6\times{x}^{2}.

Complete the calculation.

To complete the calculation, divide both sides by $6$ first, and then square root both sides to find $x.$

\begin{aligned}24\div{6}&=x^{2} \\\\ 4&=x^{2} \\\\ x&=2 \end{aligned}

Write the solution, including the units.

As the unit of area is square feet $(ft^2),$ the unit length will be in feet.

$x=2 \, ft$

Example 6: find the length of a cube given the surface area (decimal solution)

The surface area of a cube is $483 \, mm^{2}.$ Find the length of the side $x$ correct to $2$ decimal places.

Write the formula for the surface area of the cube.

S=6x^{2}

Substitute any known value(s) into the formula.

As you know the surface area, you can substitute $S=483$ into the formula $483=6\times{x}^{2}.$

Complete the calculation.

To complete the calculation, divide both sides by $6$ first, and then square root both sides to find $x.$

\begin{aligned}483\div{6}&=x^{2} \\\\ 80.5&=x^{2} \\\\ \sqrt{80.5}&=x \\\\ x&=8.972179222463… \end{aligned}

Write the solution, including the units.

x=8.97 \mathrm{~cm} \, (1 d p).

Teaching tips for surface area of a cube

When introducing the surface area of a cube, use a math net to break down the cube into individual cubes, showing that each side of a cube is a square.

Allow students time to work through a variety of problems, on worksheets or using a technology tool. Students should have time to work independently, as well as with other students, to really reinforce learning and understanding.

Use visuals and real life examples of cubes, such as a rubik’s cube, to allow students to physically hold and explore cubes.

Easy mistakes to make

Missing/incorrect units
You should always include units in your answer.
Surface area is measured in square units (for example, $\mathrm{mm}^2, \mathrm{~cm}^2, \mathrm{~m}^2$ etc.).

Calculating with different units
You need to make sure all measurements are in the same units before calculating the surface area. For example, you can’t have some in $cm$ and some in $m.$

Calculating volume instead of surface area
Volume and surface area are different quantities. The volume of the cube is the three-dimensional space in a shape and is measured in cubic units. Surface area is the amount of space covering the outside of a 3D shape. To find surface area, find the area of one face and multiply it by six.

Practice surface area of a cube questions

27 \, cm^3

12 \, cm^2

36 \, cm^2

54 \, cm^2

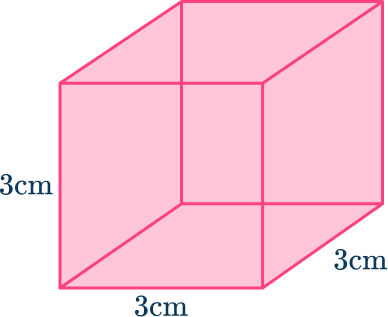
$S=6x^{2}$ where $x=3 \, cm.$

S=6\times{3}^{2}=6\times{9}=54 \, cm^{2}.

0.125 \, cm^3

15,000 \, cm^2

6 \, cm^2

1.5 \, cm^2

$S=6x^{2}$ where $x=0.5 \mathrm{~m}=50 \mathrm{~cm}.$

S=6\times{50}^{2}=6\times{2500}=15,000 \, cm^{2}.

96 \, cm^2

9,600 \, cm^2

960 \, cm^2

9.6 \, cm^2

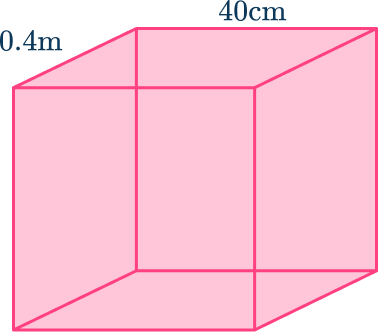
$S=6x^{2}$ where $x=40 \mathrm{~cm}=0.4 \mathrm{~m}.$

S=6\times{40}^{2}=6\times{1600}=9,600 \, cm^{2}.

135,000 \, cm

2.04 \, cm

5 \, cm

12.5 \, cm

$S=6x^{2}$ where $S=150 \, cm^{2}.$

\begin{aligned}150&=6\times{x}^{2} \\\\ 25&=x^{2} \\\\ x&=\sqrt{25} \\\\ x&=5cm \end{aligned}

2 \, m

1 \, m

0.3 \, m

0.41 \, m

$S=6x^{2}$ where $S=6 \, m^{2}.$

\begin{aligned}6&=6\times{x}^{2} \\\\ 6\div{6}&=x^{2} \\\\ x^{2}&=1 \\\\ x&=\sqrt{1} \\\\ x&=1m \end{aligned}

5.57 \, m

2.27 \, m

15.50 \, m

207,576 \, m

$S=6x^{2}$ where $S=186 \, m^{2}.$

\begin{aligned}186&=6\times{x}^{2} \\\\ 31&=x^{2} \\\\ x&=\sqrt{31}=5.567764362830…=5.57 \, (2 d p). \end{aligned}

Surface area of a cube FAQs

What is a cube?

A cube is a three-dimensional figure with six equal square faces and $8$ vertices.

What is the formula to find the volume of a cube?

To find the volume of a cube, you will use the formula $V=a^3$ or
$V=\text { side } \times \text { side } \times \text { side }.$

The next lessons are

Pythagorean theorem
Congruence and similarity
Transformations

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.