High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Multiplication and division 2D shapes Quadrilaterals Fractions Parallel lines Line segmentCongruence and similarity
Here you will learn about congruence and similarity, including what congruent shapes are and what similar shapes are. This will extend to congruent triangles and scaling.
Students will first learn about congruence and similarity as a part of geometry in 8 th grade and will expand that knowledge into high school.
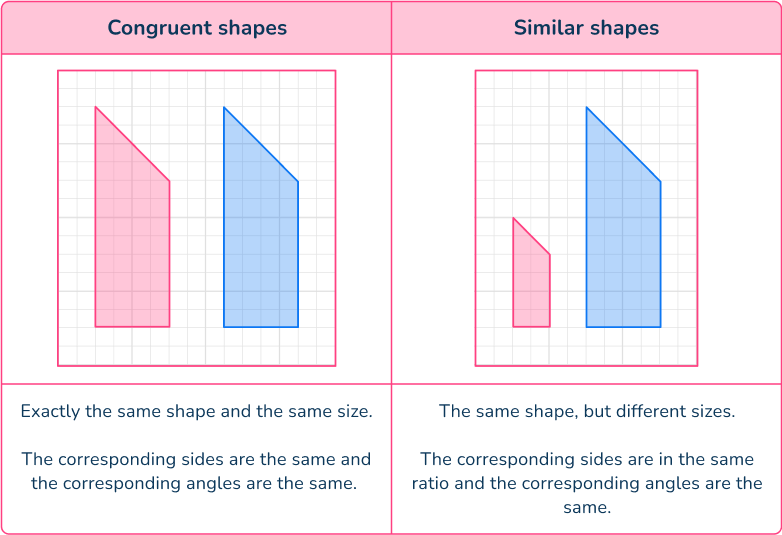
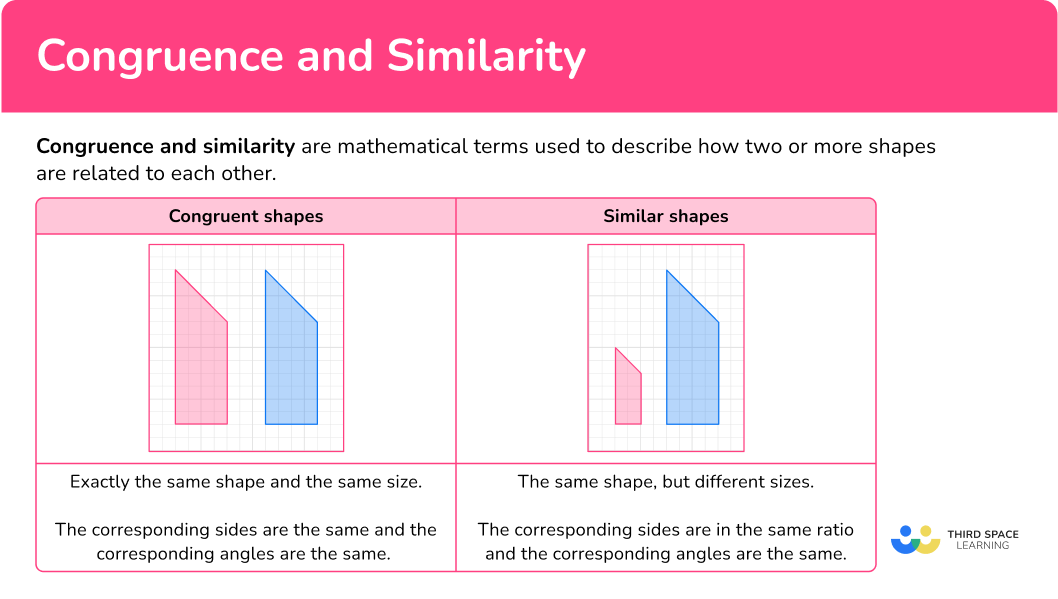
What is congruence and similarity?
Congruence and similarity are mathematical terms used to describe how two or more shapes are related to each other.
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
[FREE] Common Core Practice Tests (Grades 3 to 8)
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
Prepare for math tests in your state with these Grade 3 to Grade 8 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
DOWNLOAD FREE![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
[FREE] Common Core Practice Tests (Grades 3 to 8)
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
Prepare for math tests in your state with these Grade 3 to Grade 8 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
DOWNLOAD FREECongruent shapes
Congruent shapes are exactly the same shape and the same size.
The corresponding sides are the same and the corresponding angles are the same. Shapes can be congruent if they have been reflected or rotated.
For example, these polygons are congruent.
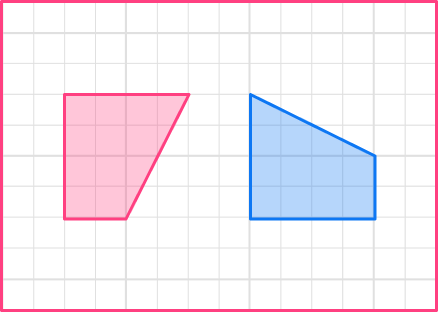
Step-by-step guide: Congruent shapes
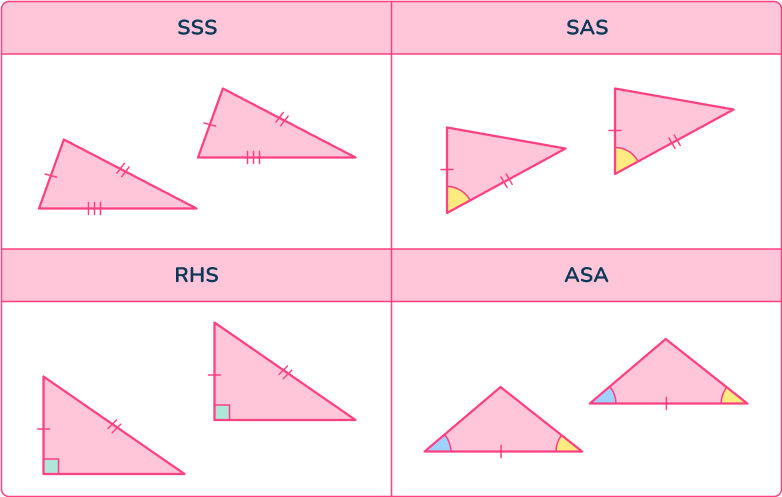
Congruent triangles
Congruent shapes can be extended to congruent triangles. There are 4 special conditions to help us recognise congruent triangles. These conditions help us prove triangle congruence.
The 4 conditions are:
SSS (side-side-side),
RHS (right-angled triangle, hypotenuse and a side),
ASA or AAS (angle-side-angle or angle-angle-side),
SAS (side-angle-side, two sides and the included angle).
Step-by-step guide: Congruent triangles
Similar shapes
Similar shapes (similar figures) are the same shape but they have different sizes. The corresponding sides are in the same ratio and the corresponding angles are the same.
If you know that 2 shapes are mathematically similar, you can find any missing sides using the ratio, or scale factor.
For example, here are 2 similar triangles.
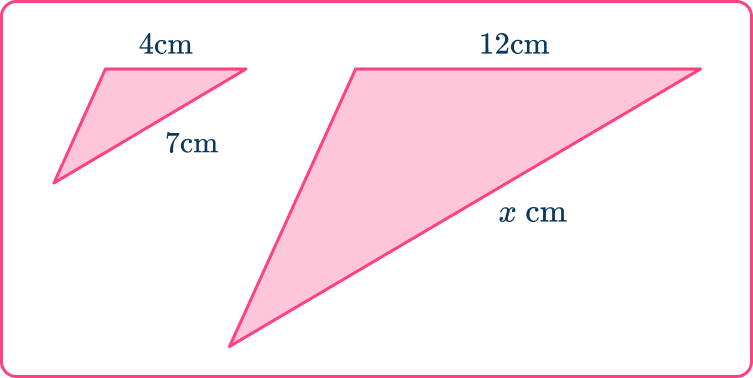
The ratio of the sides is 4\text{:}12=1\text{:}3, the scale factor is 12\div4=3.
You can use either of these to work out the size of the required length.
Therefore x=3\times 7=21.
Step-by-step guide: Similar shapes
What is congruence and similarity?
Common Core State Standards
How does this relate to 8 th grade math?
- Grade 8: Geometry (8.G.A.2)
Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
How to use congruence and similarity
There are a lot of ways to use congruence and similarity. For more specific step-by-step guides, check out the individual pages linked in the “What is congruence and similarity?” section above or read through the examples below.
Congruence and similarity examples
Example 1: congruent shapes
Are these 2D shapes congruent?
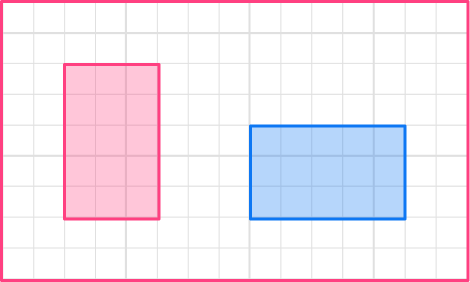
- Check the type of 2D shape.
Both shapes are rectangles.
2Check the corresponding angles and corresponding sides.
All the angles are 90^{\circ}.
The short sides on both rectangles are 3.
The long sides on both rectangles are 5.
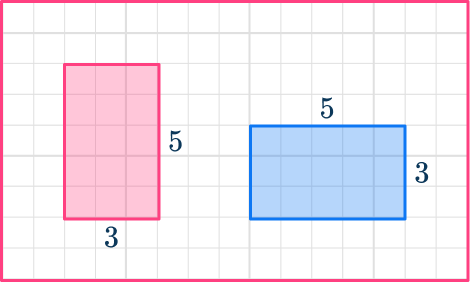
3State if the shapes are congruent or not.
The shapes are the same shape and the same size – they are congruent shapes.
Example 2: recognize congruent triangles
Decide whether this pair of triangles are congruent. If they are congruent, state why.

Check the corresponding angles and corresponding sides.
Both triangles have sides 9 \, cm.
Both triangles have a 45^{\circ} angle.
But their second angles are different.
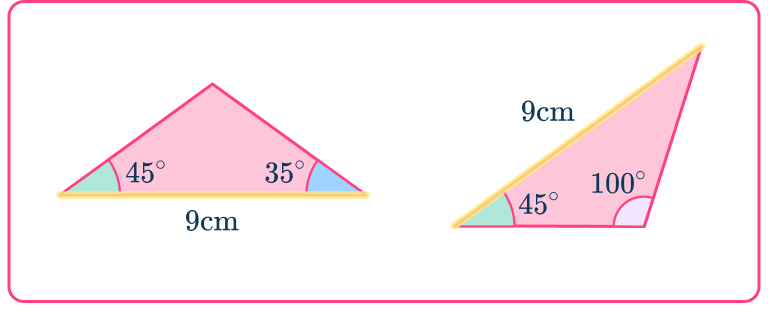
Decide if the shapes are congruent or not.
The triangles look like they are different shapes BUT the third angle can be worked out. Using the angle fact that the sum of interior angles of a triangle is 180^{\circ}, you can work out the missing angle in both triangles.
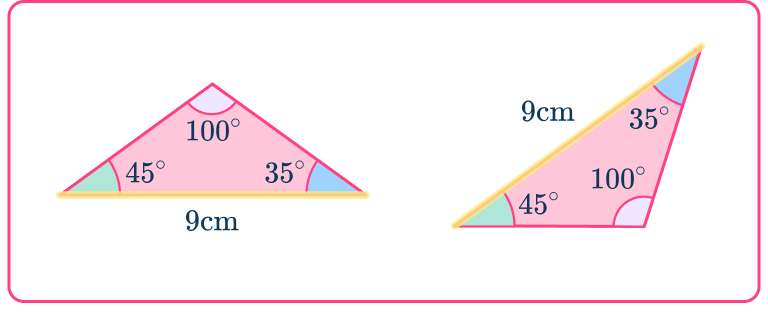
The 9 \, cm side is in between the angles 45^{\circ} and 35^{\circ} in both triangles. The triangles are the same shape and the same size. They are congruent triangles.
If the triangles are congruent, which congruence condition fits the pair of triangles.
The triangles are congruent with the condition angle-side-angle (ASA).
Example 3: prove congruent triangles (higher)
Prove that triangle ABC is congruent to triangle XYZ.
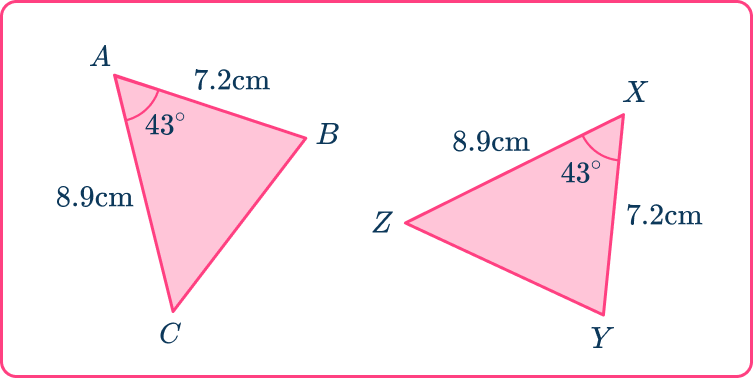
Pair up the corresponding sides.
State which sides are identical, here there are two pairs of corresponding sides.
\begin{aligned} AB &= XY \\\\ AC &= XZ \end{aligned}
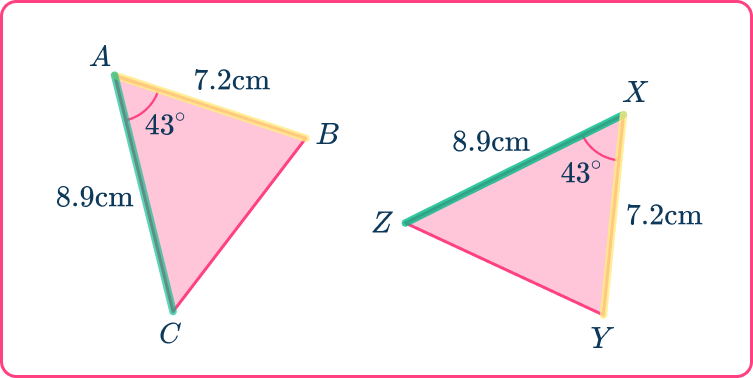
Pair up the corresponding angles.
State which angles are identical, here there is one pair of equal angles.
You need to use the correct notation.
\text { angle } C A B=\text { angle } Z X Y
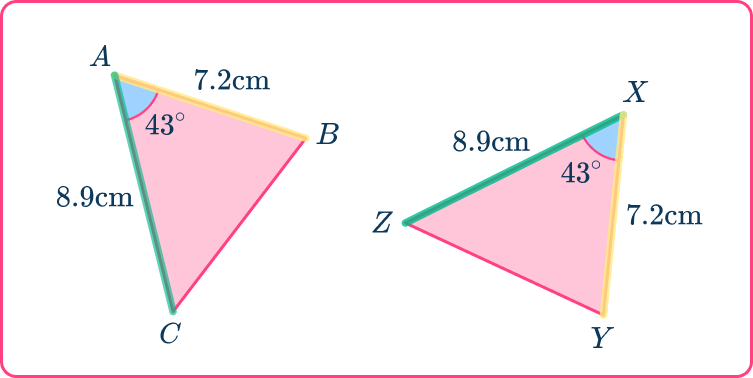
State which congruence condition fits the pair of triangles.
Triangle ABC is congruent to triangle XYZ because they fit the side-angle-side (SAS) condition.
Example 4: finding a missing length using similar shapes
Here are two similar shapes. Find the length PQ.
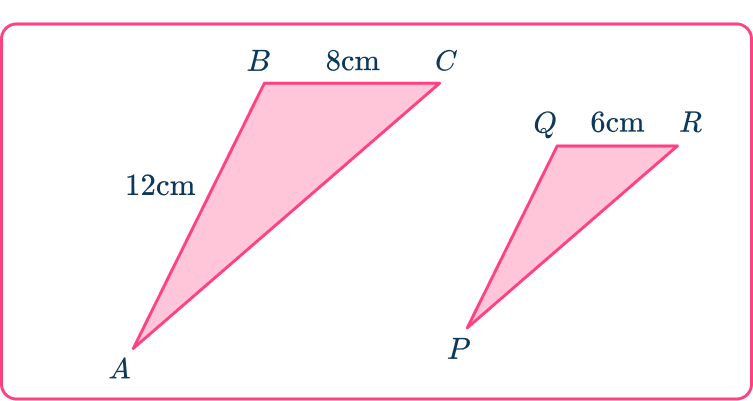
Decide which sides are pairs of corresponding sides.
Pair up the sides that have measurements. Make sure you pair up the side mentioned in the question.
The sides AB and PQ are a pair of corresponding sides.
The sides BC and QR are a pair of corresponding sides.
Find the scale factor.
The ratio of the lengths BC\text{:}QR is 8\text{:}6 which simplifies to 4\text{:}3.
This gives a scale factor of enlargement from triangle ABC to triangle PQR of \cfrac{3}{4}.
Use the scale factor to find the missing length.
The ratio of the lengths AB\text{:}PQ is also 4\text{:}3.
You can use the scale factor \cfrac{3}{4} as a multiplier to find the missing length.
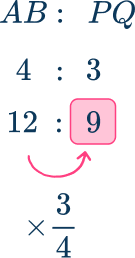
The missing side has been found, PQ=9 \, cm.
Alternatively, an equation may be formed and solved.
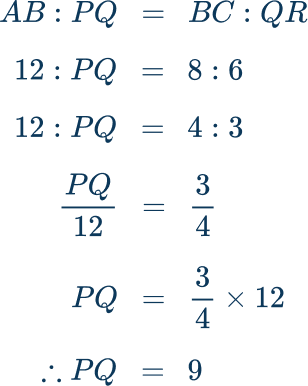
Example 5: finding a missing area using similar shapes
These two figures are similar.
The area of shape A is 10 \, cm^{2}.
Find the area of shape B.
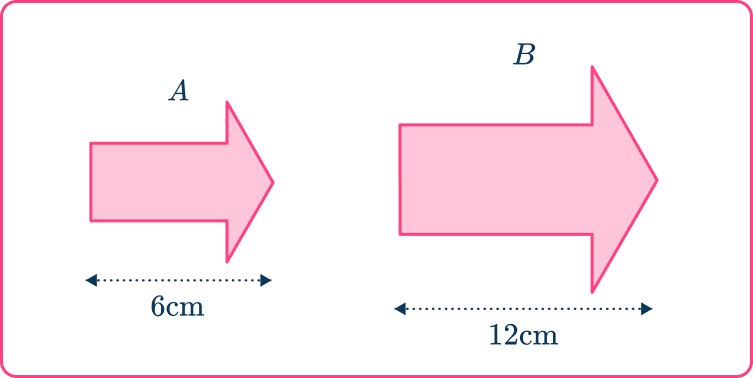
Find the scale factor.
Use the given information to write a ratio and work out the scale factor.
When writing the ratios, the order is very important.
The ratio of the lengths is \text{length } A\text{:} \, \text{length} \, B
\hspace{4.6cm} 6\text{:}12
which simplifies to \hspace{2.1cm} 1\text{:}2
The scale factor of enlargement from shape A to shape B is 2.
Use the scale factor to find the missing value.
When finding an area, you need to square the ratio of the lengths, and square the scale factor.
The ratio of the lengths is \text{ length } A\text{:} \text{ length } B
\hspace{4.7cm} 1\text{:}2
The ratio of the areas is \hspace{0.6cm} \text { area } A\text{:} \text{ area } B
\hspace{4.7cm} 1^{2}\text{:}2^{2}
which simplifies to \hspace{2.2cm} 1\text{:}4
You can use the area scale factor 2^{2} or 4 as a multiplier to find the missing area.
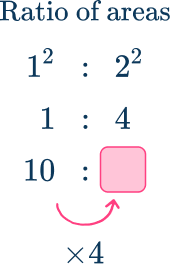
10\times 4=40
The area of shape B is 40 \, cm^{2}.
Alternatively, you can form an equation to solve.
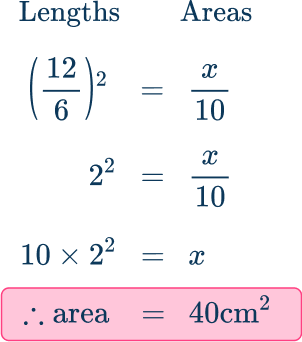
Example 6: finding a missing volume using similar shapes
These two shapes are similar.
The volume of shape A is 120 \, cm^{3}.
Find the volume of shape B.
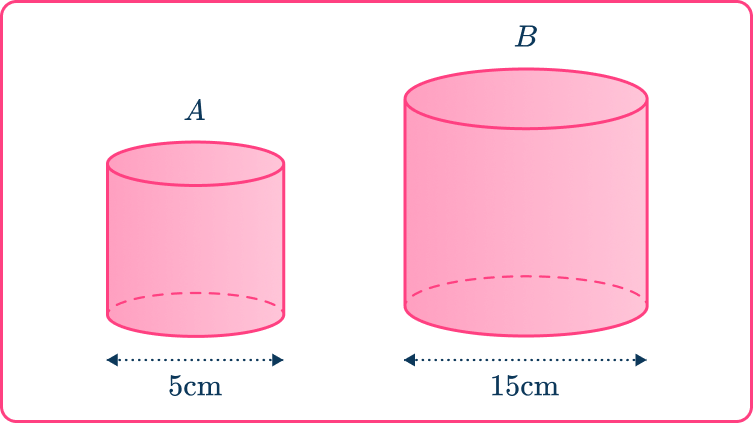
Find the scale factor.
Use the given information to write a ratio and work out the scale factor.
When writing the ratios, the order is very important.
The ratio of the lengths is \text{ length } A\text{:} \text{ length } B
\hspace{4.7cm} 5\text{:}15
which simplifies to \hspace{2.2cm} 1\text{:}3
The scale factor of enlargement from shape A to shape B is 3.
Use the scale factor to find the missing value.
When finding a volume, you need to cube the ratio of the lengths, and cube the scale factor.
The ratio of the lengths is \text{ length } A\text{:} \text{ length } B
\hspace{4.7cm} 1\text{:}3
The ratio of the volume is \text{ volume } A\text{:} \text{ volume } B
\hspace{4.75cm}1^{3}\text{:}3^{3}
which simplifies to \hspace{2.3cm}1\text{:}27
You can use the volume scale factor 3^{3} or 27 as a multiplier to find the missing volume.
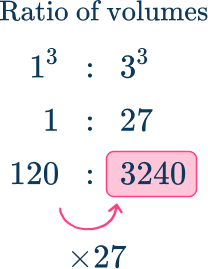
120\times 27=3240
The volume of shape B is 3240 \, cm^{3}.
Alternatively, you can form an equation to solve.
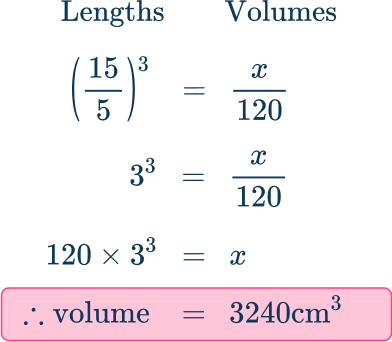
Teaching tips for congruence and similarity
- When first introducing the concept of congruence and similarity, use visual aids, including diagrams and models, that are clearly marked and demonstrate the difference between congruent shapes and similar shapes.
- There are a lot of interactive apps that are created by fellow educators that allow students to manipulate shapes to see how the transformations affect the shapes. There is also access to interactive games and quizzes that give students plenty of practice and immediate feedback.
Easy mistakes to make
- Shapes can be congruent but in different orientations
The second shape may be in a different orientation to the first shape. The shapes can still be congruent. The use of tracing paper can help you check.
- In most diagrams the diagrams are NOT drawn to scale
Questions about congruent shapes are often on grids. But sometimes diagrams may have shapes which are NOT drawn to scale. So use the measurements given, rather than measuring for yourself.
- Scaling up or down
If you are finding a missing length in the larger shape, you can multiply by the scale factor. The scale factor will be a number greater than 1.
If you are finding a missing length in the smaller shape, you can multiply by the scale factor, but the scale factor will be a number between 0 and 1.
Practice congruence and similarity questions
1. Which of these shapes is congruent to shape X?
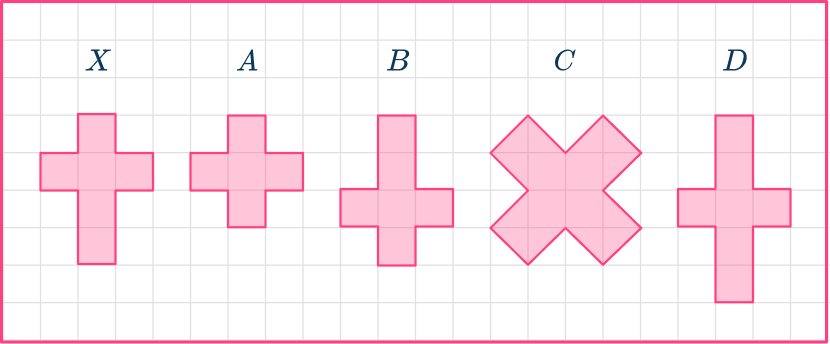




Shape B is the same as the original shape, but is upside down.
2. Here is a pair of congruent triangles. Which congruence condition is satisfied?
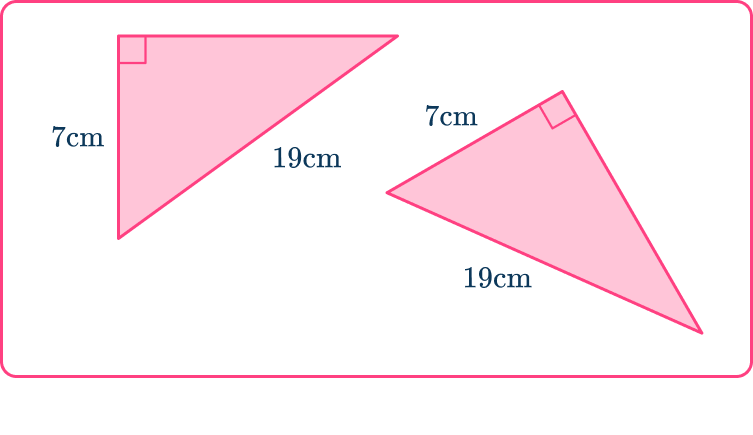




The triangles are right angle triangles. They have the same hypotenuse and the same short side.
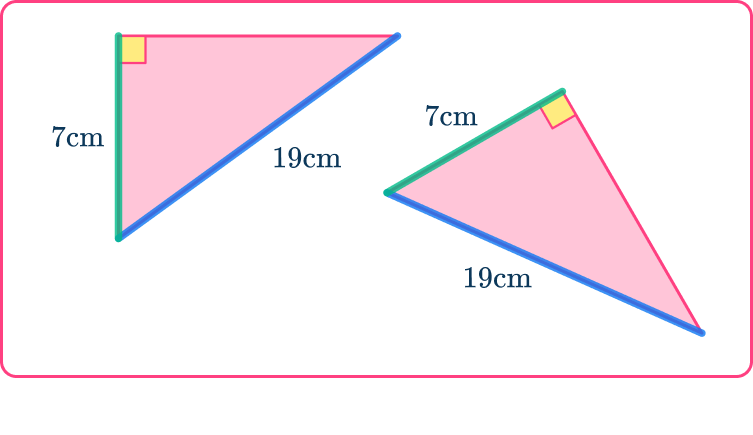
3. Prove that triangle ABD is congruent to triangle DEF.
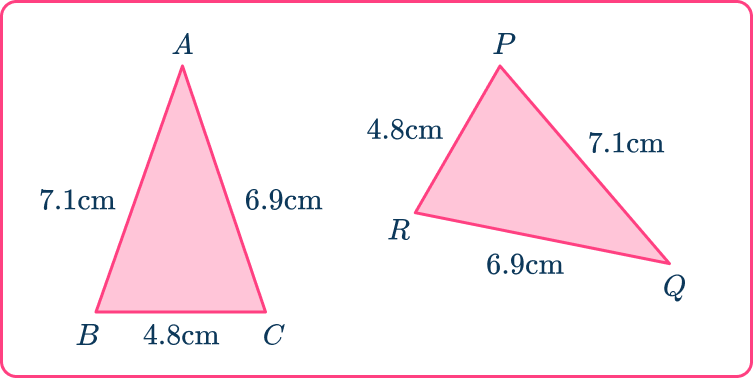
Because
\begin{aligned}AB &= PQ \\\\ AC &= RQ \\\\ BC&=PR \end{aligned}

Because
\begin{aligned}AB &= RQ \\\\ AC &= PQ \\\\ BC&=PR \end{aligned}

Because
\begin{aligned}AB &= PR \\\\ AC &= RQ \\\\ BC&=PQ \end{aligned}

Because
\begin{aligned}AB &= PR \\\\ BC&=PQ \\\\ AC &= RQ \end{aligned}

The corresponding sides need to be paired up. The lengths of sides are all equal.
4. These parallelograms are similar. Find the value of x.
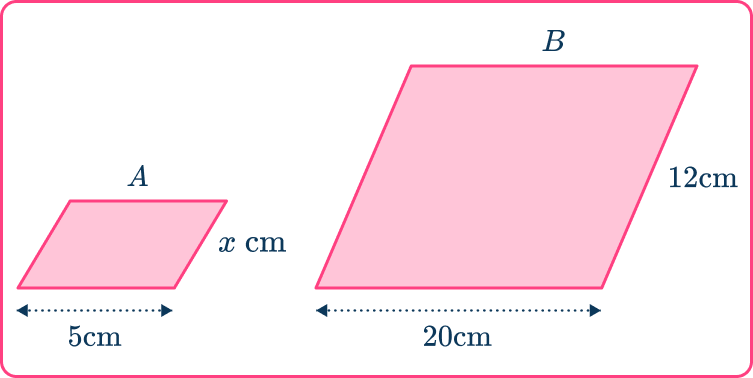




The ratio of the bases is \quad 5\text{:}20
which simplifies to \quad \quad \quad 1\text{:}4.
The scale factor of enlargement is 4. But you will need to divide by 4 as you are finding a length on the smaller shape.
x=12\div4=3
5. Here are two similar shapes. The area of shape A is 60 \, cm^{2}. Find the area of shape B.
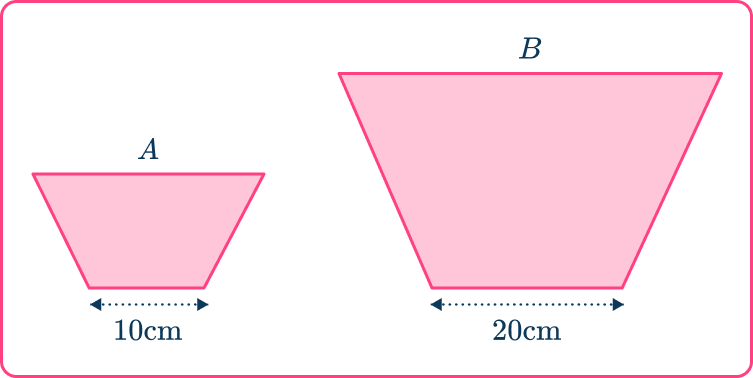




The ratio of the bases is \quad 10\text{:}20
which simplifies to \quad \quad \quad 1\text{:}2.
The scale factor of enlargement is 2. But you are finding the area, so you need to multiply the area of shape A by 2^{2} or 4.
60\times 2^2=60\times 4=240
The area of shape B is 240 \, cm^{2}.
6. Here are two similar shapes. The volume of shape B is 35,840 \, cm^{3}. Find the volume of shape A.
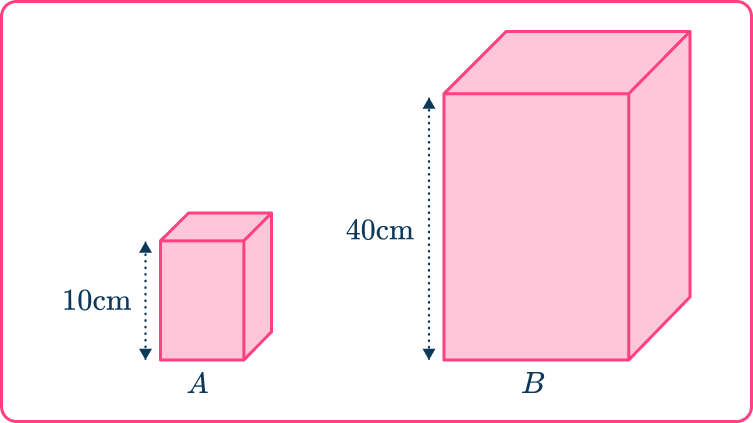




The ratio of the bases is \quad 10\text{:}40
which simplifies to \quad \quad \quad 1\text{:}4.
The scale factor of enlargement is 4. But you are finding the volume, so you need to use 4^{3} or 64.
Since you are finding the volume of the smaller shape, divide by the scale factor.
35840\div 4^3=35840\div 64=560
The volume of shape A is 560 \, cm^{3}.
Congruence and similarity FAQs
Congruent shapes are identical in both size and shape. Similar shapes have the same shape but differ in size. The corresponding angles are equal, and the corresponding sides are proportional.
You can prove two shapes are similar by using scaling combined with rotation, reflection and translation. Scaling may change the size of the shape, but will keep the shape proportional.
The scale factor is the ratio of the lengths of corresponding sides in similar shapes. It tells you how much one shape has been enlarged or reduced compared to the other. A scale factor that is larger than 1 will result in a larger shape, and a scale factor less than 1 will result in a smaller shape.
Step-by-step guide: Scale math
Step-by-step guide: Scale drawing
The next lessons are
- Transformations
- Mathematical proof
- Area
- Trigonometry
- Pythagoras’ theorem
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!