Scale Drawing

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Decimals Ratio Conversion of measurement units Multiplication and division

Equivalent ratios

Multiplying and dividing by different powers of 10

Conversion of metric units

Math resources Geometry

Congruence and similarity

Scale drawing

Here you will learn about scale drawings, including creating scale drawings, using scale factors, and solving word problems involving scale drawings.

Students will first learn about scale drawings as part of geometry in $7$ th grade.

What is a scale drawing?

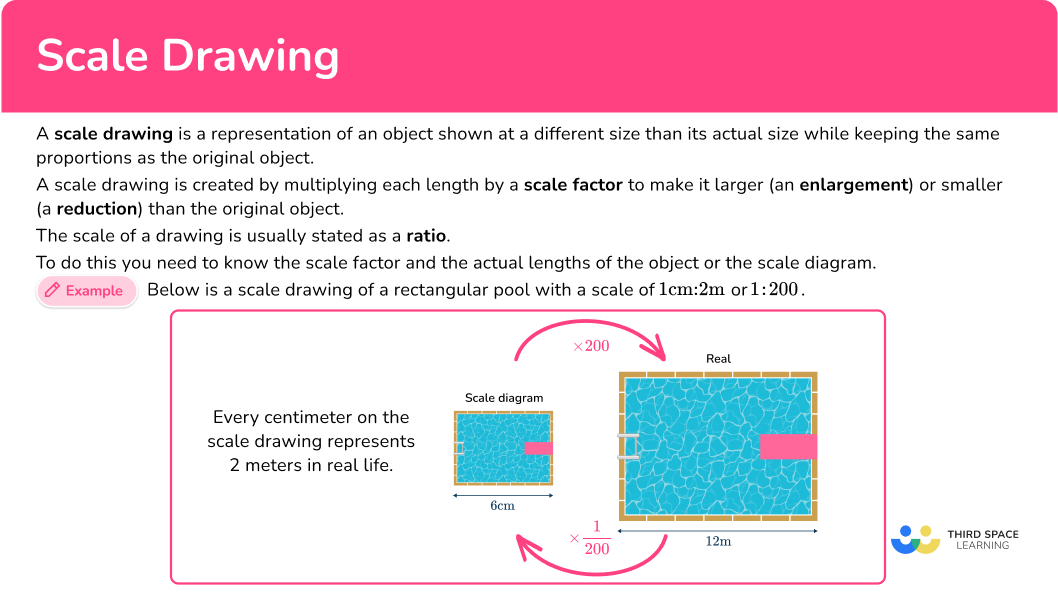
A scale drawing is a representation of an object shown at a different size than its actual size while keeping the same proportions as the original object.

A scale drawing is created by multiplying each length by a scale factor to make it larger (an enlargement) or smaller (a reduction) than the original object.

The scale of a drawing is usually stated as a ratio. For example, $1 \, cm \, \text{:} \, 5 \, m.$ You would read this as “ $1$ centimeter to $5$ meters” which means that every $1$ centimeter on the diagram represents $5$ meters in real life.

In order to interpret and produce scale drawings, you need to know the scale factor and the actual lengths of the object.

For example, below is a scale drawing of a rectangular pool with a scale of $1 \, cm \, \text{:} \, 2 \, m$ or $1 \, \text{:} \, 200.$ This means that every centimeter on the diagram represents $2$ meters (or $200 \, cm$ ) in real life.

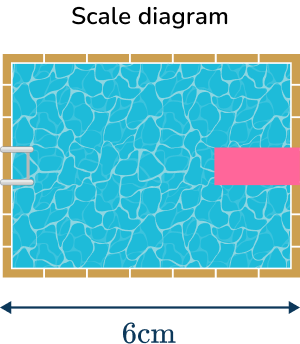
The width of the pool in the diagram is $6 \, cm,$ so the width of the real life pool is $12 \, m.$

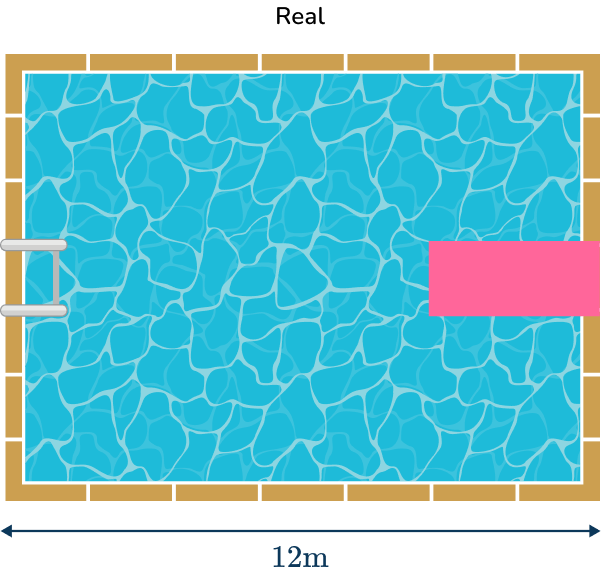
The actual dimensions of the pool have been enlarged by a scale factor of $\cfrac{1}{200}$ to give the scale drawing.

The scale drawing has been enlarged by a scale factor of $200$ to get the actual dimensions of the pool.

The majority of scale drawing questions will involve polygons or 2D drawings such as floor plans or using a map although there is overlap with topics such as enlargement, construction of triangles, and loci.

What is a scale drawing?

Common Core State Standards

How does this relate to $7$ th grade math?

Grade 7 – Geometry (7.G.A.1)
Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

DOWNLOAD FREE

[FREE] Common Core Practice Tests (Grades 3 to 6)

DOWNLOAD FREE

How to calculate the actual distance from a scale

In order to calculate the actual distance from a scale:

State the scale of the enlargement as a ratio in the form $\bf{{1} \, \text{:} \, \textbf{n.}}$
Multiply $\textbf{n}$ by the length given from the scale drawing.
Write the units.

Scale drawing examples

Example 1: map

A map has a scale of $1 \, cm \, \text{:} \, 2 \, km.$ Find the actual distance in kilometers represented by $5 \, cm$ on the map.

State the scale of the enlargement as a ratio in the form $\bf{{1} \, \text{:} \, \textbf{n.}}$

1 \, cm \, \text{:} \, 2 \, km.

2Multiply $\textbf{n}$ by the length given from the scale drawing.

2\times{5}=10

3Write the units.

10 \, km.

Example 2: plan of a building

A plan for a block of apartments has the scale $2.5 \, cm \, \text{:} \, 800 \, m.$ What is the real distance represented by $5.7 \, cm$ on the plan?

State the scale of the enlargement as a ratio in the form $\bf{{1} \, \text{:} \, \textbf{n.}}$

Dividing both sides by $2.5$ to get the same units first, you get

$1 \, cm \, \text{:} \, 320 \, m.$

Multiply $\textbf{n}$ by the length given from the scale drawing.

320\times{5.7}=1,824

Write the units.

1,824 \, m

Example 3: atlas

A world atlas has a scale of $2 \, cm \, \text{:} \, 5 000 \, km.$ Calculate the real world distance that is represented by $23 \, mm$ on the atlas.

State the scale of the enlargement as a ratio in the form $\bf{{1} \, \text{:} \, \textbf{n.}}$

As the length required is in millimeters, you first need to change the $2 \, cm$ to millimeters.

\begin{aligned}&2\mathrm{~cm} \, \text{:} \, 5 000\mathrm{~km} \\\\ &=20\mathrm{~mm} \, \text{:} \, 5 000\mathrm{~km}\end{aligned}

Then you can reduce the ratio so you have $1 \, mm \, \text{:} \, n \, km.$ Dividing both sides by $20,$ you get:

$1 \, mm \, \text{:} \, 250 \, km$

Multiply $\textbf{n}$ by the length given from the scale drawing.

250\times{23}=5750

Write the units.

5750 \, km

How to calculate the scale drawing distance from a scale

In order to calculate the scale drawing distance from a scale:

State the scale of the enlargement as a ratio in the form $\bf{{1} \, \text{:} \, \textbf{n.}}$
Divide the real life distance by the scale ratio.
Write the units.

Example 4: model object

A model car is made using the model to an actual distance of $1 \, cm \, \text{:} \, 40 \, cm.$ The height of the car is $170 \, cm.$ Calculate the height of the model car.

State the scale of the enlargement as a ratio in the form $\bf{{1} \, \text{:} \, \textbf{n.}}$

The ratio given is $1 \, \text{:} \, 40.$

Divide the real life distance by the scale ratio.

170\div{40}=4.25

Write the units.

4.25 \, cm

Example 5: floor plan

A plan of a kitchen uses the scale $1 \, cm \, \text{:} \, 0.2 \, m.$ Calculate the distance on the plan for the actual distance of $5.62 \, m.$

State the scale of the enlargement as a ratio in the form $\bf{{1} \, \text{:} \, \textbf{n.}}$

The ratio is already in the form $1 \, \text{:} \, n.$

$1 \, cm \, \text{:} \, 0.2 \, m$

Divide the real life distance by the scale ratio.

5.62\div{0.2}=28.1

Write the units.

28.1 \, cm

Example 6: map of the UK

A map of the UK is drawn using the scale $50 \, cm \, \text{:} \, 1400 \, km.$ Calculate how far $8 \, 680 \, 000 \, cm$ would be on the map.

State the scale of the enlargement as a ratio in the form $\bf{{1} \, \text{:} \, \textbf{n.}}$

First convert $8 \, 680 \, 000 \, cm$ to $km.$

$8 \, 680 \, 000 \, cm = 86 \, 800 \, m = 86.8 \, km.$

Now $50 \, cm \, \text{:} \, 86.8 \, km.$

Let’s convert the ratio to the form $1 \, cm \, \text{:} \, n \, km$ by dividing both sides of the ratio by $50.$

\begin{aligned}&50\mathrm{~cm} \text{:} \, 1400\mathrm{~km}\\\\&=1\mathrm{~cm} \, \text{:} \, 28\mathrm{~km}\end{aligned}

Divide the real life distance by the scale ratio.

Now you can calculate the length on the map

$86.8\div{28}=3.1$

Write the units.

3.1 \, cm

Teaching tips for scale drawing

Provide students with rulers and graph paper to create their own scaled drawings.

Create worksheets (printable or online/interactive) that use real life examples where scale drawings are used, such as maps or blueprints. This helps students understand the practical application of scale drawing.

Introduce students to different scales, such as $1 \, \text{:} \, 10, \, 1 \, \text{:} \, 50,$ or $1 \, \text{:} \, 100,$ and explain how they affect the size of the drawing relative to the actual object.

Connect scale drawing to real world situations relevant to students’ lives. For example, ask students to solve problems involving designing their dream bedroom or creating a floor plan for their house. This makes the concept more relatable and engaging.

Incorporate technology such as online scale drawing software or apps that allow students to create and manipulate scale drawings digitally instead of on a piece of paper.

Easy mistakes to make

Multiplying the real life distance by the ratio scale
The real life distance is multiplied by the ratio scale, giving an incorrect distance on the plan.

Dividing the model / plan / map distance by the ratio scale
The distance on the model / plan / map is divided by the ratio scale meaning that the real life distance is incorrect.

Not simplifying the ratio scale
If given the ratio $2 \, cm \, \text{:} \, 5 \, km,$ it is easier to calculate when the ratio is in the form $1 \, \text{:} \, n$ and so you must find an equivalent ratio before using the scale. Here the ratio would be $1 \, cm \, \text{:} \, 2.5 \, km$ so $1 \, cm$ on the map would be equal to $2.5 \, km$ in real life.

Incorrect units in the solution
The units for the model are mixed up with the units for the real life distance. For example, if you were calculating the distance of $10 \, cm$ on a map with the scale ratio of $1 \, cm \, \text{:} \, 5 \, km, \, 10\times{5}=50\mathrm{~cm}$ is stated whereas the correct solution would be $10\times{5}=50\mathrm{~km}.$

Converting units
Sometimes the units need to be converted so that you are working with the same units, making calculations much easier to comprehend. Make sure you know how to convert between different metric units.

For example, the map scale is given as $1 \, \text{:} \, 25,000$ which means that $1 \, cm$ on the map is equivalent to $25,000 \, cm$ in real life.

If the answer is asked to be written in kilometers, the real life value in centimeters must be divided by $100,000$ to get the same measurement in kilometers. $1 \, \text{:} \, 25,000=1\mathrm{~cm} \text{:} \, 0.25\mathrm{~km}$

Congruence and similarity
Congruent shapes
Congruent triangles
Similar shapes
Scale math

Practice scale drawing questions

0.86 \, km

0.86 \, cm

10.5 \, km

10.5 \, cm

3\times{3.5}=10.5\mathrm{~km}

3750 \, km

7500 \, km

33.3 \, km

3750 \, cm

2\mathrm{~cm} \, \text{:} \, 500\mathrm{~km}=1\mathrm{~cm} \, \text{:} \, 250\mathrm{~km}

250\times{15}=3750\mathrm{~km}

10.738 \, m

10.738 \, cm

107.38 \, m

3.08 \, m

1 \, cm \, \text{:} \, 1.82 \, m

1.82\times{5.9}=10.738\mathrm{~m}

0.39 \, cm

0.39 \, m

4.96 \, cm

4.96 \, m

\begin{aligned}&138.8\mathrm{~cm}=1.388\mathrm{~m} \\\\ &10\mathrm{~cm} \, \text{:} \, 2.8\mathrm{~m}=1\mathrm{~cm} \, \text{:} \, 0.28\mathrm{~m} \\\\ &1.388\div{0.28}=4.96\mathrm{~cm} \end{aligned}

1.061 \, m

13.26 \, m

10.61 \, m

1.326 \, m

13 \, 200 \, 000\mathrm{~cm}=132\mathrm{~km}

8\mathrm{~m} \, \text{:} \, 1400\mathrm{~km}=1\mathrm{~m} \, \text{:} \, 175 \mathrm{~km}

175\div{132}=1.326\mathrm{~m} \, \text{ (3 dp)}

28 \, cm

6.22 \, m

6.22 \, cm

25.2 \, cm

0.9\mathrm{~cm} \, \text{:} \, 20\mathrm{~cm}=1\mathrm{~cm} \, \text{:} \, 22.\bar{2}\mathrm{~cm}

The model to the actual distance ratio is therefore $1\mathrm{~cm} \, \text{:} \, 22.\bar{2}\mathrm{~cm}$

5.6\mathrm{~m}=560\mathrm{~cm}

560\div22.\bar{2}=25.2\mathrm{~cm}

Scale drawing FAQs

What is a scale drawing?

A scale drawing is a representation of an object shown at a different size than its actual size while keeping the same proportions as the original object.

How do you create a scale drawing?

A scale drawing is created by multiplying each length by a scale factor to make it larger (an enlargement) or smaller (a reduction) than the original object.

Why are scale drawings used?

Scale drawings are used to represent objects or spaces at a different size than their actual size while keeping accurate proportions, which helps with visualization, planning, communication, and problem-solving.

For example, an architect may draw the floor plan of a building at a smaller scale than the actual building size in order to plan out and visualize the design before starting construction.

The next lessons are

Transformations
Mathematical proof
Area

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.