High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Converting metric units
Here you will learn about converting metric units, including metric units of length, metric units of mass and metric units of capacity (volume).
Students will first learn about converting metric units as part of measurement and data in 4 th grade and 5 th grade.
What is converting metric units?
Converting metric units is being able to convert between different metric units of measurement (including length, mass and volume).
To do this, you need to know what the metric units are and their conversion factors.
Certain prefixes are used before the base unit to show bigger and smaller metric units. They can help us remember the metric conversions.

- Metric units of length
The SI unit (international system of units) of length is the meter (m).
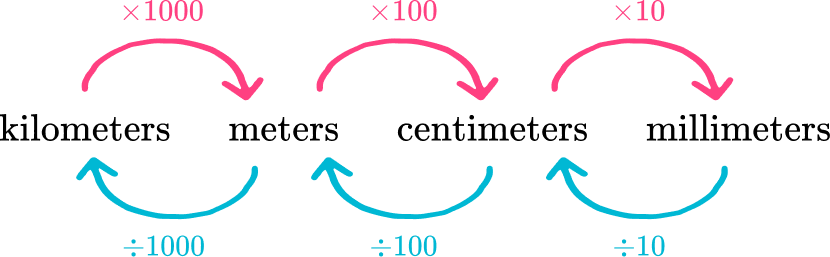
For example,
Covert 7 meters (m) to centimeters (cm).
Looking at the diagram above, meters can be converted to centimeters by multiplying by 100.
7 \mathrm{~m} \times 100=700 \mathrm{~cm}
- Metric units of mass
The metric system for mass is based around grams (g).
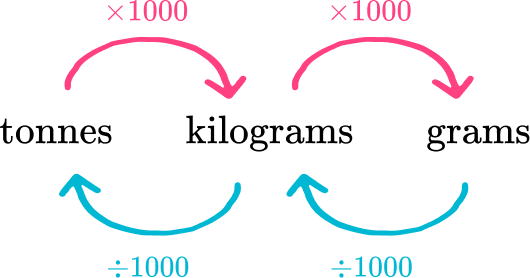
For example,
Covert 4 kilograms (kg) to grams (g).
Looking at the diagram above, kilograms can be converted to grams by multiplying by 1000.
4 \mathrm{~kg} \times 1000=4000 \mathrm{~g}
- Metric units of capacity (volume)
The metric system for capacity is based on liters (l).
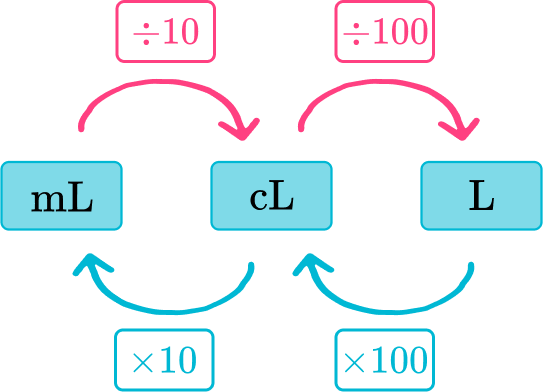
For example,
Covert 6,000 milliliters (ml) to liters (l).
Looking at the diagram above, milliliters can be converted to liters by dividing by 10 then dividing by 100, which is equal to dividing by 1,000.
6,000 \mathrm{~ml} \div 1,000=6 \mathrm{~l}
What is converting metric units?
Common Core State Standards
How does this relate to 4 th grade math and 5 th grade math?
- Grade 4 – Measurement and Data (4.MD.A.1)
Know relative sizes of measurement units within one system of units including km, m, cm; kg, g; lb, oz.; l, ml; hr, min, sec. Within a single system of measurement, express measurements in a larger unit in terms of a smaller unit. Record measurement equivalents in a two- column table.
For example, know that 1 \, ft is 12 times as long as 1 \, in. Express the length of a 4 \, ft snake as 48 \, in. Generate a conversion table for feet and inches listing the number pairs (1, 12), (2, 24), (3, 36), …
- Grade 5 – Measurement and Data (5.MD.A.1)
Convert among different-sized standard measurement units within a given measurement system (for example, convert 5 \, cm to 0.05 \, m ), and use these conversions in solving multi-step, real world problems.
How to convert metric units
In order to convert metric units:
- Find the unit conversion.
- Multiply or divide.
- Write the answer.
![[FREE] Units of Measurement Check for Understanding (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Units-of-Measurement-listing-image.png)
[FREE] Units of Measurement Check for Understanding (Grade 4 to 5)
![[FREE] Units of Measurement Check for Understanding (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Units-of-Measurement-listing-image.png)
Use this quiz to check your grade 4 to 5 students’ understanding of units of measurement. 10+ questions with answers covering a range of 4th and 5th grade units of measurement topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Units of Measurement Check for Understanding (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Units-of-Measurement-listing-image.png)
[FREE] Units of Measurement Check for Understanding (Grade 4 to 5)
![[FREE] Units of Measurement Check for Understanding (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Units-of-Measurement-listing-image.png)
Use this quiz to check your grade 4 to 5 students’ understanding of units of measurement. 10+ questions with answers covering a range of 4th and 5th grade units of measurement topics to identify areas of strength and support!
DOWNLOAD FREEConverting metric units examples
Example 1: converting length
Convert 3.2 \mathrm{~m} to cm.
- Find the unit conversion.
1 \mathrm{~m}=100 \mathrm{~cm}
2Multiply or divide.
Look at the relationship in the original conversion.

From meters to centimeters, the relationship is multiplying by 100.
Multiply 3.2 meters by 100\text{:}
3.2 \text { meters } \times 100=320 \text { centimeters }
3Write the answer.
3.2 \mathrm{~m}=320 \mathrm{~cm}
Example 2: converting length
Convert 780 \mathrm{~mm} to cm.
Find the unit conversion.
10 \mathrm{~mm}=1 \mathrm{~cm}
Multiply or divide.
Look at the relationship in the original conversion.
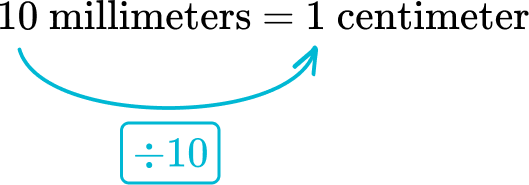
From millimeters to centimeters, the relationship is dividing by 10.
Divide 780 millimeters by 10\text{:}
780 \text { millimeters } \div 10=78 \text { centimeters }
Write the answer.
780 \mathrm{~mm}=78 \mathrm{~cm}
Example 3: converting mass
Convert 12.5 \mathrm{~kg} to g.
Find the unit conversion.
1 \mathrm{~kg}=1,000 \mathrm{~g}
Multiply or divide.
Look at the relationship in the original conversion.
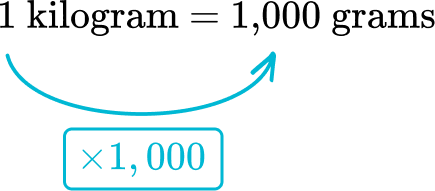
From kilograms to grams, the relationship is multiplying by 1,000.
Multiply 12.5 kilograms by 1,000\text{:}
12.5 \text { kilograms } \times 1,000=12,500 \text { grams }
Write the answer.
12.5 \mathrm{~kg}=12,500 \mathrm{~g}
Example 4: converting mass
Convert 3,800 \mathrm{~g} to kg.
Find the unit conversion.
1 \mathrm{~kg}=1,000 \mathrm{~g}
Multiply or divide.
Look at the relationship in the original conversion.
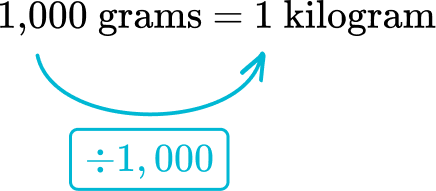
From grams to kilograms, the relationship is dividing by 1,000.
Divide 3,800 grams by 1,000\text{:}
3,800 \text { grams } \div 1,000=3.8 \text { kilograms }
Write the answer.
3,800 \mathrm{~g}=3.8 \mathrm{~kg}
Example 5: converting capacity
Convert 7.1 \mathrm{~l} to ml.
Find the unit conversion.
1,000 \mathrm{~ml}=1 \, l
Multiply or divide.
Look at the relationship in the original conversion.
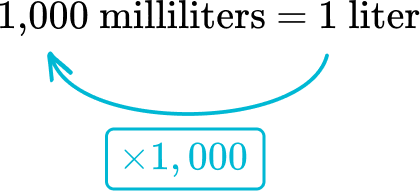
From liters to milliliters, the relationship is multiplying by 1,000.
Multiply 7.1 liters by 1,000\text{:}
7.1 \text { liters } \times 1,000=7,100 \text { milliliters }
Write the answer.
7.1 \mathrm{~l}=7,100 \mathrm{~ml}
Example 6: converting capacity
Convert 750 \mathrm{~ml} to l.
Find the unit conversion.
1 \mathrm{~l}=1,000 \mathrm{~ml}
Multiply or divide.
Look at the relationship in the original conversion.
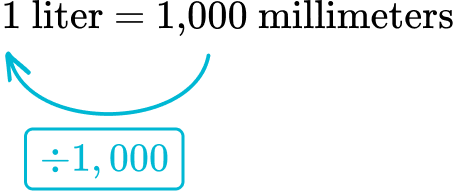
From milliliters to liters, the relationship is dividing by 1,000.
Divide 750 milliliters by 1,000\text{:}
750 \text { milliliters } \div 1,000=0.75 \text { liters }
Write the answer.
750 \mathrm{~ml}=0.75 \, l
Teaching tips for converting metric units
- Begin by providing students with many real world measurement experiences. This can include measuring the same object in multiple units, like the weight of a stack of books in grams, centigrams, and kilograms, or activities that require students to discuss the most appropriate units to use.
Once students have a good foundation in how to measure metric units and their relative sizes, they are ready to start converting.
- Instead of directly telling students about the patterns in metric conversions, wait to see when they notice them as they work with them. Given enough practice converting, the patterns in the placement of the decimal point or the number of zeroes is something many students will pick up on.
Once they begin discussing this, you can highlight this pattern as a class and keep track of what students are noticing on the white board or an anchor chart. With time, you can formalize this idea with students and connect it to the powers of 10 and/or our base 10 place value system.
- Worksheets can be a useful tool to help students practice, but ensure that the worksheet includes many different units, not just the most common ones. This is a good way for students to practice converting all units in the metric system and make use of less common prefixes, like deci.
- For students that are struggling, give them time to work with a conversion calculator that completes the conversion for them. Have them explain each conversion, including why the units changed and what equation was used.
Once they become more comfortable, they can begin solving conversions on their own. However, it may be a good idea to give them access to a conversion chart until they have memorized all the conversion factors.
Easy mistakes to make
- Not knowing whether to multiply or divide
In order to decide which operation to use, look at the original conversion. Notice how the number representing the measurement changes from one unit to another. This will show you whether to multiply or divide. The general rule for this is:- from larger units to smaller units – multiply
- from smaller units to larger units – divide
- Forgetting about uncommon units
The metric system has a new unit for each power of 10. However, within each base unit there are common units and uncommon units.
For example,
In units of weight, the most commonly used units are grams, milligrams, and kilograms. However, there are also centigrams, decigrams, and many other units.
In units of capacity, the most commonly used units are liters and milliliters. However, there are also kiloliters, centiliters, and many other units.
- Adding or subtracting to convert
The relationship between units is multiplicative, which is why multiplication and division are used to convert. Using addition or subtraction will not correctly convert between units.
Related units of measurement lessons
Practice converting metric units questions
1. Convert: 390 \mathrm{~cm} to m




Look at the relationship in the original conversion.

From centimeters to meters, the relationship is dividing by 100.
Divide 390 centimeters by 100\text{:}
390 \text { centimeters } \div 100=3.9 \text { meters }
2. Convert: 57 \mathrm{~cm} to mm




Look at the relationship in the original conversion.
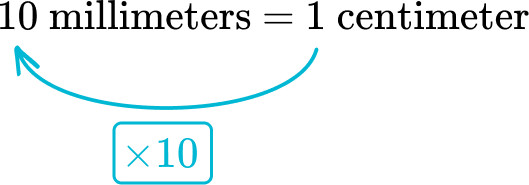
From centimeters to millimeters, the relationship is multiplying by 10.
Multiply 57 centimeters by 10\text{:}
57 \text { centimeters } \times 10=570 \text { millimeters }
3. Convert: 81,000 \mathrm{~g} to kg




Look at the relationship in the original conversion.
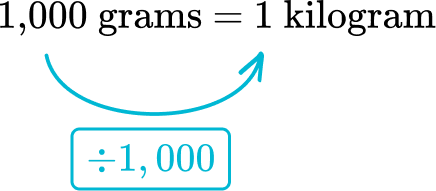
From grams to kilograms, the relationship is dividing by 1,000.
Divide 81,000 grams by 1,000\text{:}
81,000 \text { grams } \div 1,000=81 \text { kilograms }
4. Convert: 630 \mathrm{~kg} to tonnes




Look at the relationship in the original conversion.
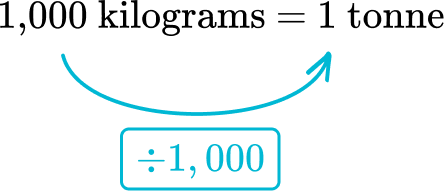
From kilograms to tonnes, the relationship is dividing by 1,000.
Divide 630 kilograms by 1,000\text{:}
630 \text { kilograms } \div 1,000=0.63 \text { tonnes }
5. Convert: 4.8 \mathrm{~l} to ml




Look at the relationship in the original conversion.
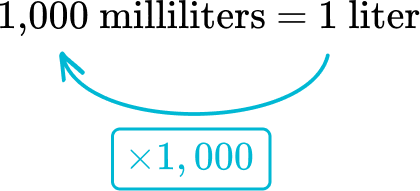
From liters to milliliters, the relationship is multiplying by 1,000.
Multiply 4.8 liters by 1,000\text{:}
4.8 \text { liters } \times 1,000=4,800 \text { milliliters }
6. Convert: 560 \mathrm{~ml} to l




Look at the relationship in the original conversion.
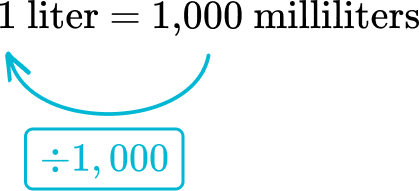
From milliliters to liters, the relationship is dividing by 1,000.
Divide 560 milliliters by 1,000\text{:}
560 \text { milliliters } \div 1,000=0.56 \text { liters }
Converting metric units FAQs
The customary system is a different measurement system. Some examples of customary units are inches, feet, ounces, pounds, cups and gallons. This system of measurement is commonly used in the United States.
Yes, any measurement that is not a complete unit can be shown with a fraction or a decimal.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!