High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
2D shapes Angles of a triangle Pythagorean theoremCoordinates
Congruent triangles
Here you will learn about congruent triangles, including how to identify them and prove the congruence of triangles.
Students will first learn about congruent triangles as part of geometry in eighth grade and again in high school geometry.
What are congruent triangles?
Congruent triangles are triangles that are exactly the same size and shape.
There are 4 conditions to prove congruency in triangles.
Side-side-side (SSS)
When two triangles have all three sides the same, they are congruent triangles.
The second triangle may be a rotation or a mirror image of the first triangle (or both).

![[FREE] Congruent Triangles Worksheet (Grade 6 And High School)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Congruent-Triangles-Worksheet-listing-image.png)
[FREE] Congruent Triangles Worksheet (Grade 6 And High School)
![[FREE] Congruent Triangles Worksheet (Grade 6 And High School)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Congruent-Triangles-Worksheet-listing-image.png)
Use this worksheet to check your 6th grade and high school students’ understanding of congruent triangles. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Congruent Triangles Worksheet (Grade 6 And High School)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Congruent-Triangles-Worksheet-listing-image.png)
[FREE] Congruent Triangles Worksheet (Grade 6 And High School)
![[FREE] Congruent Triangles Worksheet (Grade 6 And High School)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Congruent-Triangles-Worksheet-listing-image.png)
Use this worksheet to check your 6th grade and high school students’ understanding of congruent triangles. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREERight angle, hypotenuse and one other side (RHS)
When two triangles are right-angled triangles and have the hypotenuse and one of the shorter sides the same, they are congruent triangles.
The second triangle may be a rotation or a mirror image of the first triangle (or both). The third side would also be identical and this can be checked using Pythagoras’ theorem.

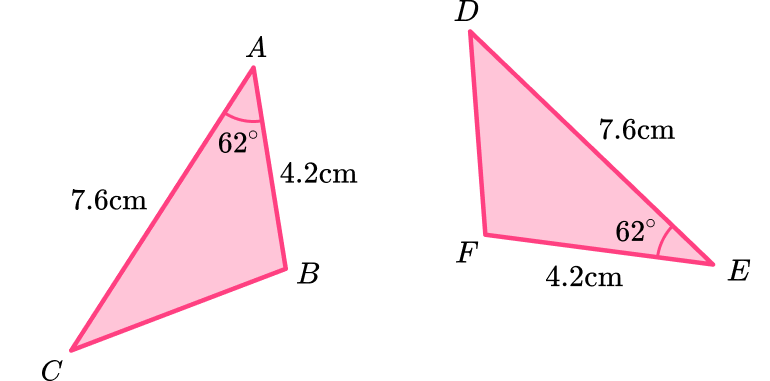
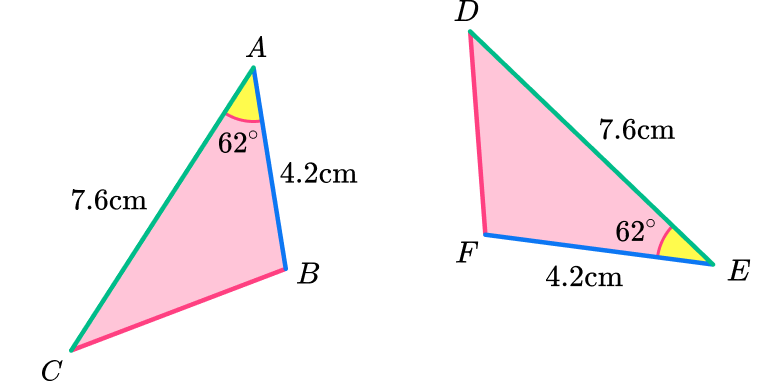
Side-angle-side (SAS)
When two triangles have two sides and the included angle the same, they are congruent triangles. The included angle is the angle in between the two sides.
The second triangle may be a rotation or a mirror image of the first triangle (or both).

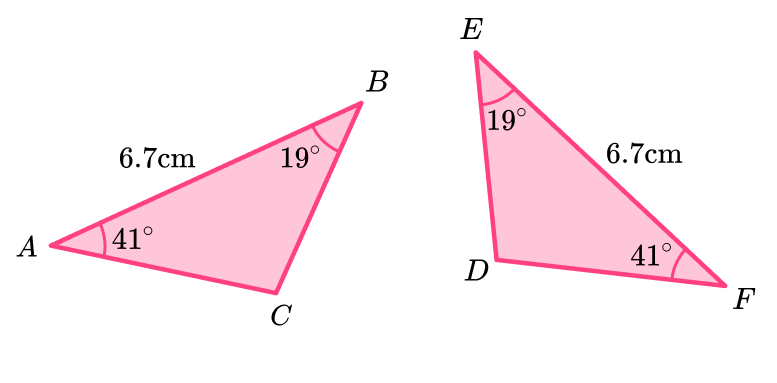
Angle-side-angle (ASA)
When two triangles have two angles and the included side the same, they are congruent triangles. The included side is the side in between the two angles.
The second triangle may be a rotation or a mirror image of the first triangle (or both).

This can also be known as angle-angle-side (AAS) , as if two angles in a triangle are known, the third angle can be worked out using the angle fact that the sum of interior angles in a triangle is 180^{\circ}.
What are congruent triangles?

Common Core State Standards
How does this relate to 8 th grade and high school?
- Grade 8 – Geometry (8.G.A.2)
Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
- High school – Similarity, right triangles and trigonometry (9-12.HSG-SRT.B.5)
Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures.
How to recognize congruent triangles
In order to recognize if a pair of triangles are congruent:
- Check the corresponding angles and corresponding sides.
- Decide if the polygons are congruent or not.
- If the triangles are congruent, state which congruence condition fits the pair of triangles.
Congruent triangles examples
Example 1: recognize congruent triangles
Decide whether this pair of triangles are congruent. If they are congruent, state why:
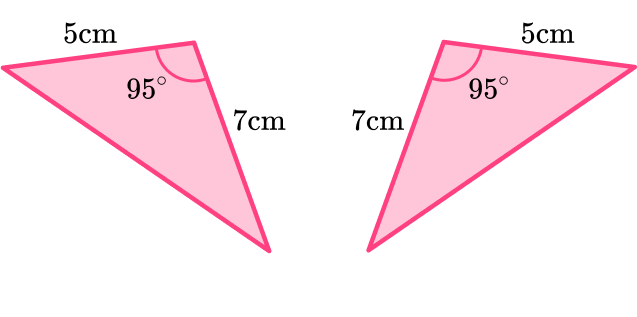
- Check the corresponding angles and corresponding sides.
Both triangles have sides 5~{cm} and 7~{cm}. They both have an angle of 95^{\circ}.
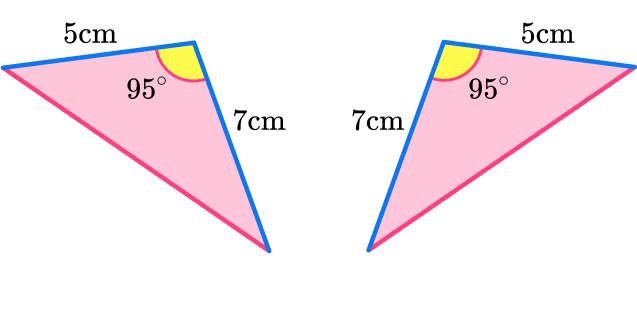
2Decide if the polygons are congruent or not.
The 95^{\circ} angles are in a corresponding position. The triangles are mirror images of each other. The triangles are congruent.
3If the triangles are congruent, state which congruence condition fits the pair of triangles.
The triangles are congruent with the condition side-angle-side \textbf{(SAS)}.
Example 2: recognize congruent triangles
Decide whether this pair of triangles are congruent. If they are congruent, state why:
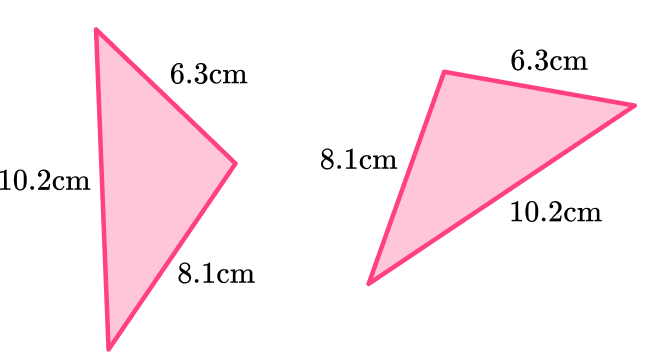
Check the corresponding angles and corresponding sides.
Both triangles have sides 6.3~{cm}, 8.1~{cm} and 10.2~{cm}.
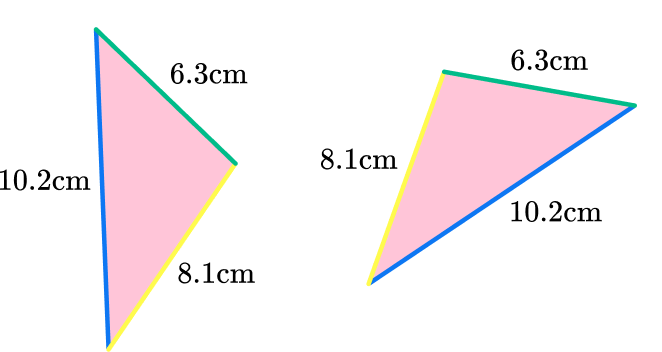
Decide if the polygons are congruent or not.
The triangles are the same shape and the same size – they are congruent.
If the triangles are congruent, state which congruence condition fits the pair of triangles.
The triangles are congruent with the condition side-side-side \textbf{(SSS)}.
Example 3: recognize congruent triangles
Decide whether this pair of triangles are congruent. If they are congruent, state why:
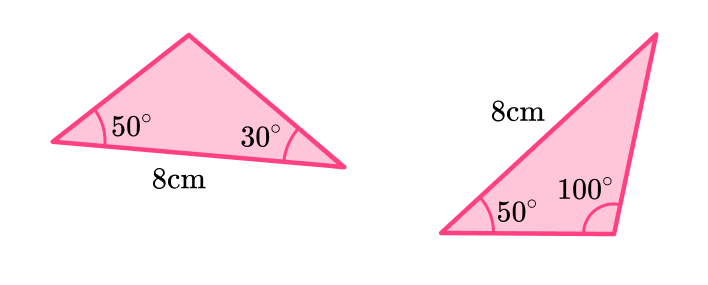
Check the corresponding angles and corresponding sides.
Both triangles have sides 8~{cm}.
Both triangles have a 50^{\circ} angle.
But their second angles are different.
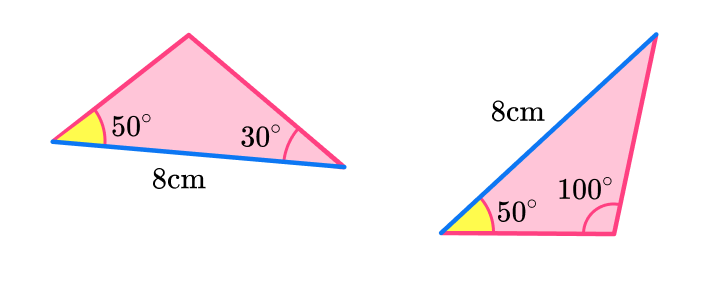
Decide if the polygons are congruent or not.
The triangles look like they are different shapes BUT the third angle measure can be worked out.
Using the angle fact that the sum of the interior angles of a triangle is 180^{\circ} , you can work out the missing angle measure in both triangles.
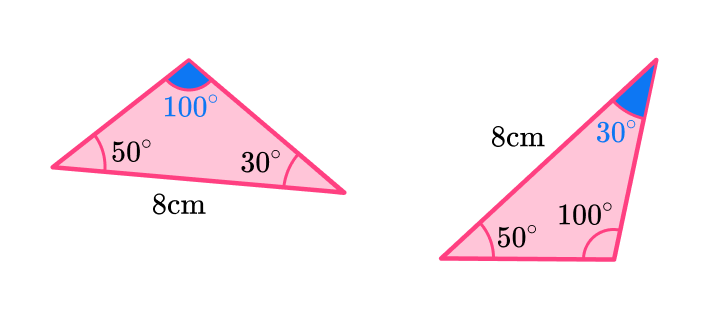
The 8~{cm} side is in between the 30^{\circ} and 50^{\circ} angles in both triangles. The triangles are the same shape and the same size.
They are congruent triangles.
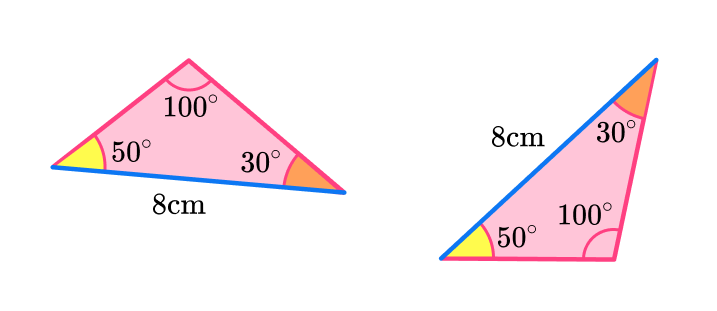
If the triangles are congruent, state which congruence condition fits the pair of triangles.
The triangles are congruent with the condition angle-side-angle \textbf(ASA) .
Example 4: recognize congruent triangles
Decide whether this pair of triangles are congruent. If they are congruent, state why:
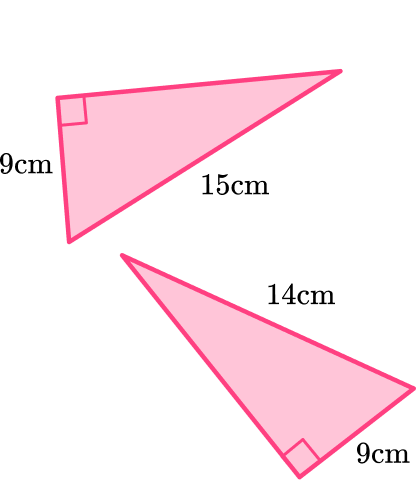
Check the corresponding angles and corresponding sides.
Both triangles are right-angled triangles.
They both have a short side of 9~{cm}.
But the hypotenuse of each triangle is different.
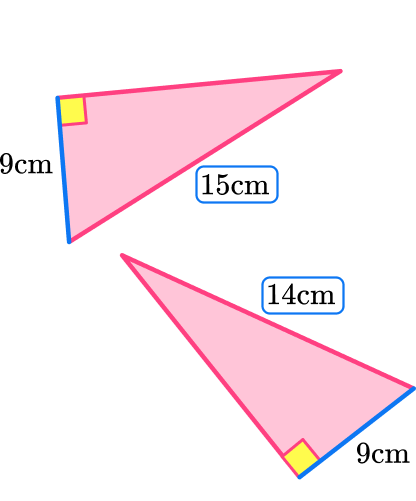
Decide if the polygons are congruent or not.
The triangles look like they are the same shape, but they are not. The triangles are NOT congruent.
If the triangles are congruent, state which congruence condition fits the pair of triangles.
The triangles are NOT congruent.
The right angle, hypotenuse and one other side (RHS) condition was close to being satisfied, but not quite.
How to prove congruent triangles
In order to prove that a pair of triangles are congruent:
- Pair up the corresponding sides.
- Pair up the corresponding angles.
- State which congruence condition fits the pair of triangles.
Proving congruent triangles examples
Example 5: prove triangles are congruent
Prove that triangle ABC is congruent to triangle DEF.
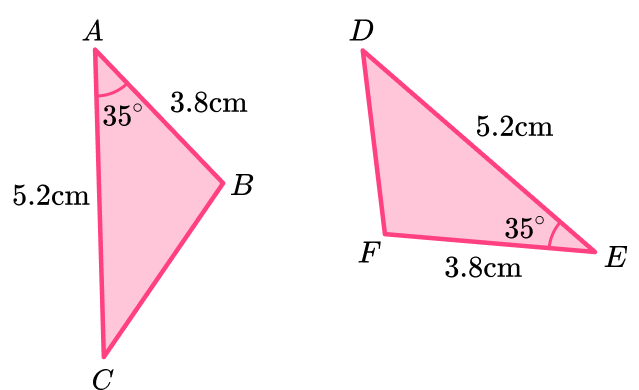
Pair up the corresponding sides.
State which sides are identical, here there are two pairs of corresponding sides.
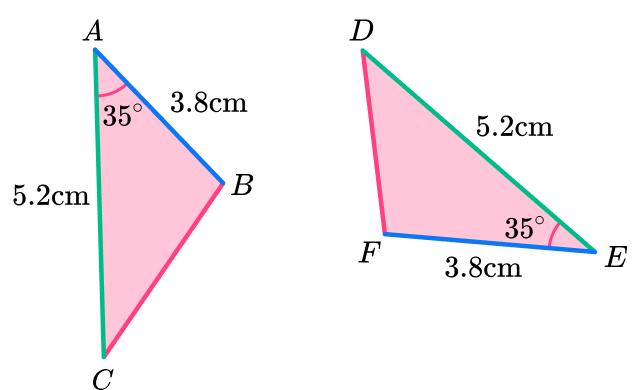
Pair up the corresponding angles.
State which angles are identical, here there is one pair of congruent angles.
You need to use the correct notation.
\text{angle} \ CAB = \text{angle} \ DEF
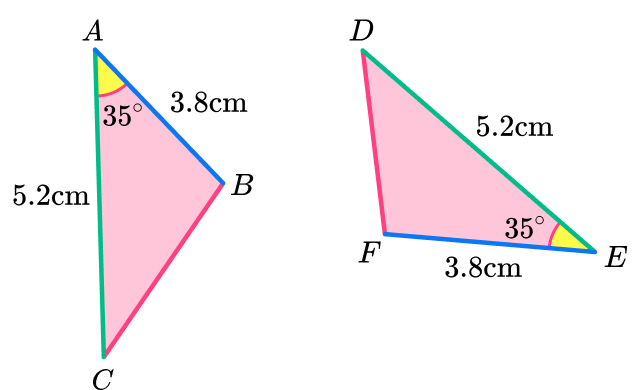
State which congruence condition fits the pair of triangles.
Triangle ABC is congruent to triangle DEF because they fit the side-angle-side \textbf{(SAS)} condition.
Example 6: prove triangles are congruent
Prove that triangle ABD is congruent to triangle BCD
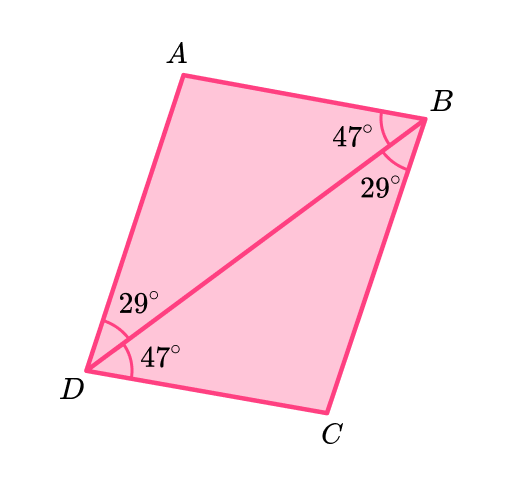
Pair up the corresponding sides.
State which sides are identical, here there is one pair of corresponding sides. It is the common side.
BD is common

Pair up the corresponding angles.
State which angles are identical, here there are two pairs of equal angles. You need to use the correct notation.
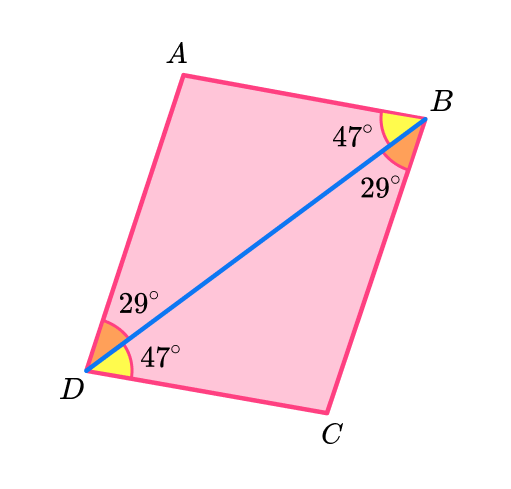
State which congruence condition fits the pair of triangles.
Triangle ABD is congruent to triangle BCD because they fit the angle-side-angle \textbf{(ASA)} condition.
Teaching tips for congruent triangles
- Use models and manipulatives. Having students physically move triangles around to see how they match up, even when oriented differently, makes the concept more concrete. Tools like Geogebra, Desmos, geometric solids, and triangle cutouts facilitate hands-on triangle comparisons.
- Focus on corresponding parts. Students must deeply understand that for triangle congruence, it’s not about any three angles or sides overall being equal, but rather matching angles and sides specifically “corresponding” between the triangles that must be equivalent. Use coloring, labels, and worksheets to indicate these correlations.
- Incorporate real-world examples. Provide images of congruent objects students see everyday—folded paper, signs, architecture shapes. Ask questions like “How do you know these triangles within the structures are congruent?” to encourage practical applications.
- Use proper math language. Reinforce vocabulary terms like corresponding, congruent, transformation, orientation, etc. alongside having students articulate triangle congruence postulates and proofs clearly using if-then logic and proper notations. Saying “these triangles match” is too vague—accurate language is key!
Easy mistakes to make
- Assuming three angles being equal is a condition for triangle congruence
A common mistake is incorrectly assuming that just because two triangles have the same three angle measurements, it means the triangles must be congruent. However, having identical angles is not sufficient – the corresponding sides of the triangles also need to be equal in length for them to be congruent.
- Not recognizing rotations or mirror images as congruent triangles
A triangle may be a rotation or a mirror image of the first shape (or both). The triangle may still be congruent. A common error is not realizing that congruent triangles can be in different orientations – they do not necessarily have to be positioned the same way.
- Incorrectly naming angles
When referring to angles within a triangle, it is important to use the proper mathematical notation instead of informal names. For instance, consider a triangle labeled ABC that contains a 50 degree angle. It would be wrong to call this " Angle B."
In mathematical terminology, the appropriate way to name this angle is " angle ABC" or " angle CBA," which clearly identifies the vertex point and the side endpoints that delineate the angle. Calling it by a simple letter risks ambiguity and reduces precision, which can lead to flawed conclusions about triangle congruence.
- Not giving enough details on proof questions
When attempting to prove two triangles congruent, it is essential to demonstrate the logic and evidence that verifies their equality. Simply stating the triangles are congruent without sufficient supportive details will likely result in lost credit.
For example, consider a proof problem requiring you to confirm ∆ABC ≅ ∆DEF. It is not enough to merely assert “These triangles have corresponding equal angles and sides, therefore they are congruent.”
Related congruence and similarity lessons
Practice congruent triangles questions
1) Here is a pair of congruent triangles. Which congruence condition is satisfied?





The triangles are right triangles. They have the same hypotenuse-leg and the same non-included side.

2) Here is a pair of congruent triangles. Which congruence condition is satisfied?





The triangles have two identical sides and an identical included angle.
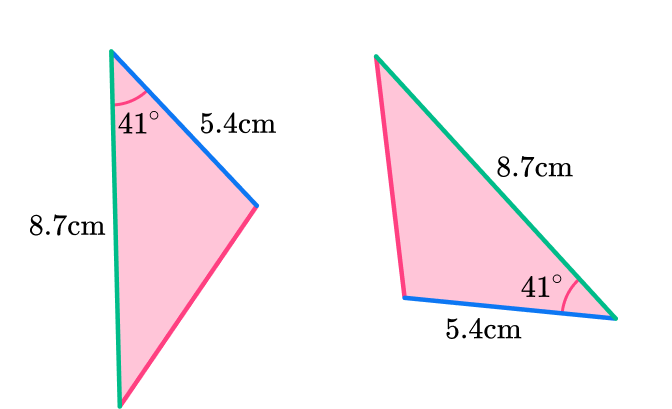
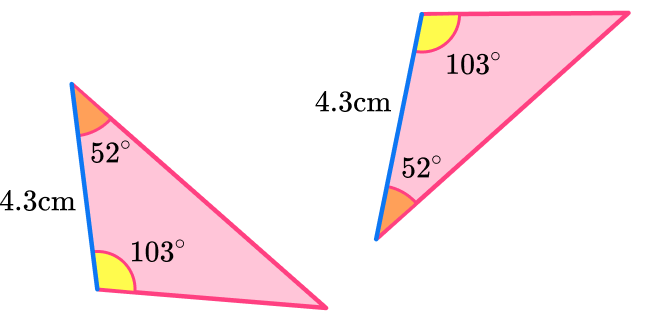
3) Here is a pair of congruent triangles. Which congruence condition is satisfied?
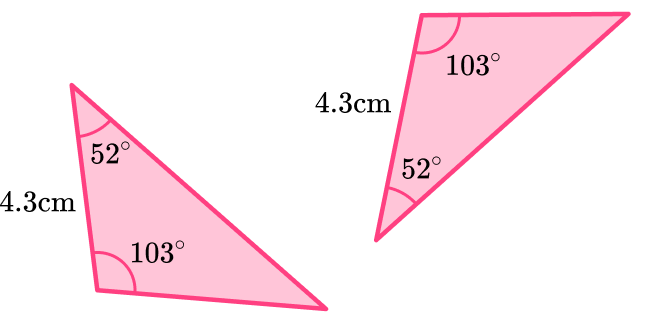




The triangles have two identical angles and an identical included side.
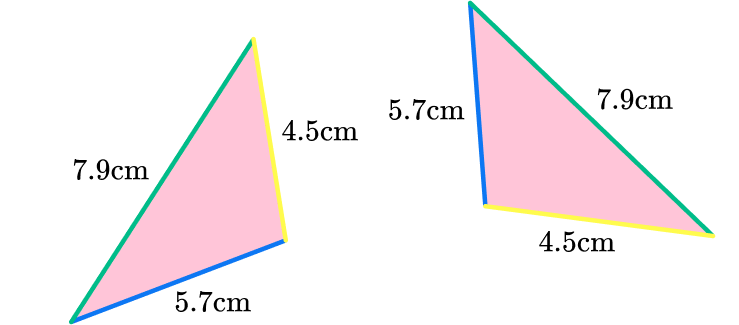
4) Here is a pair of congruent triangles. Which congruence condition is satisfied?
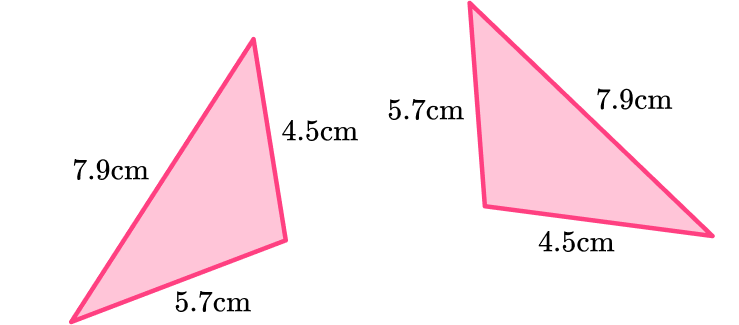




The triangles have three identical sides.
5) Prove that triangle ABC is congruent to triangle DEF.
because
\begin{aligned} &AB = EF \\ &AC = DE\\ &\text{angle} \ CAB= \text{angle} \ DEF \end{aligned}
because
\begin{aligned} &AB = EF \\ &AC = DF\\ &\text{angle} \ A= \text{angle} \ E \end{aligned}
because
\begin{aligned} &AB = EF \\ &BC = DE\\ &\text{angle} \ ABC= \text{angle} \ DEF \end{aligned}
because
\begin{aligned} &AB = EF \\ &AC = DF\\ &\text{angle} \ ABC= \text{angle} \ DEF \end{aligned}
The correct sides need to be paired up. The correct notation needs to be used for the angles.
6) Prove that triangle ABC is congruent to triangle DEF.
because
\begin{aligned} &AB = EF \\ &\text{angle} \ CAB= \text{angle} \ DFE\\ &\text{angle} \ BAC= \text{angle} \ DEF \end{aligned}
because
\begin{aligned} &AB = DE \\ &\text{angle} \ CAB= \text{angle} \ EFD\\ &\text{angle} \ CBA= \text{angle} \ DEF \end{aligned}
because
\begin{aligned} &AB= EF \\ &\text{angle} \ CAB= \text{angle} \ DFE\\ &\text{angle} \ CBA= \text{angle} \ DEF \end{aligned}
because
\begin{aligned} &AB = EF \\ &\text{angle} \ A= \text{angle} \ F\\ &\text{angle} \ B= \text{angle} \ E \end{aligned}
The correct sides need to be paired up. The correct notation needs to be used for the angles.
Congruent triangles FAQs
There are three main criteria for triangle congruence. If two triangles meet any one of these three criteria, they are considered congruent.
● Side-Side-Side (SSS) criterion: Two triangles are congruent if all three of their corresponding side lengths are equal.
● Side-Angle-Side (SAS) criterion: Two triangles are congruent if two of their corresponding side lengths and the angle between those sides are equal.
● Angle-Angle-Side (AAS) criterion: Two triangles are congruent if two of their corresponding angles and the side between those angles are equal.
In the case of right triangles, the Pythagorean theorem means that we can calculate the length of the third leg given the lengths of any other two.
So right triangles are a special case of the Side-Side-Side criterion where we only need two pairs of congruent side lengths.
● Hypotenuse-Leg (HL) criterion: Two right triangles are congruent if their hypotenuse lengths are equal and the lengths of one of their legs are equal.
We don’t need a Leg-Leg criterion for right triangles, because that would just be another case of Side-Angle-Side congruence.
The triangle congruence criteria help us compare and work with other figures in several ways. First, they allow us to determine whether two triangles are congruent, which can be helpful when we want to determine whether two other figures are also congruent.
Second, the triangle congruence criteria can help us break down other figures into triangles, which can be easier to work with. For example, we might divide a quadrilateral into two triangles, determine whether the two triangles are congruent, and then use that information to infer something about the quadrilateral.
Lastly, the triangle congruence criteria can also help us solve problems involving other figures by allowing us to use properties of congruent triangles. For example, if we know that two triangles are congruent, we can use the corresponding parts of the congruent triangles to find missing measurements in one of the figures.
The simple answer is that these two methods don’t always work. Side-Side-Angle (SSA) seems like it could work, but it’s possible to have two triangles with the same angle and two side measurements that aren’t congruent.
The same goes for Angle-Angle-Angle (AAA). Two triangles can have the same three angles but not be congruent.
This is why we use the four methods that do work: Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) for right triangles.
These methods have been proven to work every time, so we can rely on them to show that two triangles are congruent.
The next lessons are
- Transformations
- Mathematical proof
- Area
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!