High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Area of a rectangle Area of a parallelogram Area of a trapezoid Area of a rhombusInterior angles in polygons
Pythagorean TheoremArea of a hexagon
Here you will learn about the area of a hexagon, including how to find the area of regular hexagons and irregular hexagons.
Students will first learn about the area of a hexagon as part of geometry in high school.
What is the area of a hexagon?
The area of a hexagon is the amount of space inside a hexagon. A hexagon is a 2 D shape also known as a six-sided polygon.
Area of a regular hexagon
A regular hexagon is a polygon that has 6 sides of equal length and 6 equal interior angles.
The area of a regular hexagon can be found by splitting the shape into congruent triangles, by finding the midpoint of the shape and creating line segments.
You can find the area of one of the triangles and then multiply by the number of sides to find the total area of the regular polygon. This method will work for a regular hexagon, a regular octagon and so on. In the case of a regular hexagon, the triangles will be equilateral triangles.
The area of a regular hexagon can be simplified into the formula,
\text{Area of regular hexagon}=6\times \text{Area of one triangle}.
The area of the triangle can be found using the formula,
A=\cfrac{1}{2} \; bh.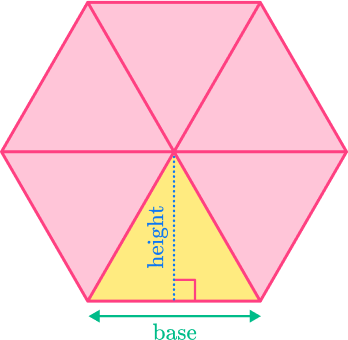
Where b is the base length (or the side of the hexagon) and h is the perpendicular height of the triangle. Sometimes these values will need to be calculated.
This means the area of a regular hexagon can also be written as,
\text{Area of regular hexagon}=6\times \cfrac{1}{2} \; bh=3bh.![[FREE] Area Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
[FREE] Area Worksheet (Grade 4 to 6)
![[FREE] Area Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 to 6 students’ understanding of area. 15+ questions with answers covering a range of 4th, 6th and 7th grade area topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Area Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
[FREE] Area Worksheet (Grade 4 to 6)
![[FREE] Area Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 to 6 students’ understanding of area. 15+ questions with answers covering a range of 4th, 6th and 7th grade area topics to identify areas of strength and support!
DOWNLOAD FREEArea of an irregular hexagon
An irregular hexagon may have been formed by different shapes. The area of a hexagon can be calculated by working out the area of each of these shapes and adding them together.
For example,
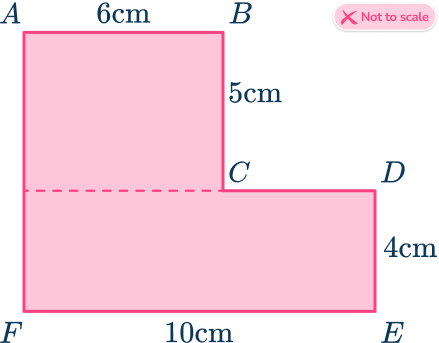
Area of the irregular hexagon ABCDEF is,
\text{Total area}=(6\times 5)+(4\times 10)=30+40=70 \ cm^2.Angles in a regular hexagon
In order to work out the angles in a regular hexagon, you can use the angle fact that states ‘the sum of angles at a point is 360^{\circ}.
All 6 congruent triangles meet at the center of the hexagon, forming a point, therefore all 6 angles around that center point should sum to 360^{\circ}.
A regular hexagon can be split into 6 congruent equilateral triangles. So, the internal angles of an equilateral triangle are all 60^{\circ}.
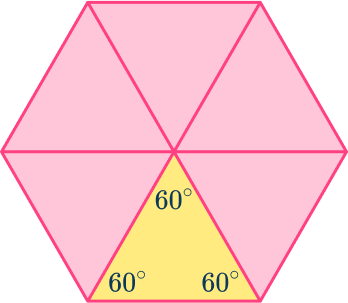
The interior angles of these congruent triangles can be used in trigonometry to find the area of each of the equilateral triangles.
Two 60^{\circ} angles make one of the interior angles of a regular hexagon, so each of the 6 interior angles is 120^{\circ}.
What is the area of a hexagon?

Common Core State Standards
How does this relate to high school math?
- High School: Geometry (HS.G.MD.A.1)
Use geometric shapes, their measures, and their properties to describe objects (e.g., modeling a tree trunk or a human torso as a cylinder).
- High School: Geometry (HS.G.SRT.D.11)
Understand and apply the Law of Sines and the Law of Cosines to find unknown measurements in right and non-right triangles (e.g., surveying problems, resultant forces).
How to find the area of a hexagon
In order to find the area of a hexagon:
- Consider the hexagon as a compound shape and split it appropriately.
- Calculate the area of the parts.
- Calculate the total area of the hexagon.
- Write the answer, including the correct units.
Area of a hexagon examples
Example 1: irregular hexagon
Find the area of the irregular hexagon ABCDEF.
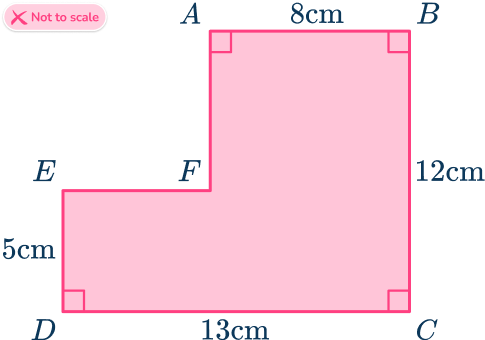
- Consider the hexagon as a compound shape and split it appropriately.
You can split the ‘L’ shape into two rectangles.
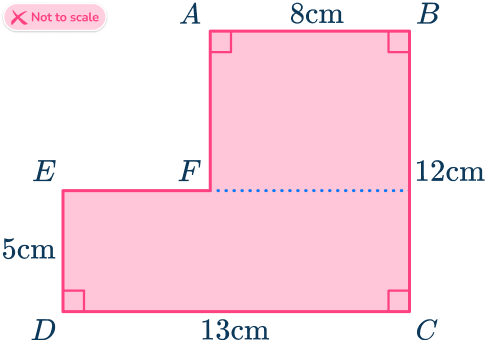
2Calculate the area of the parts.
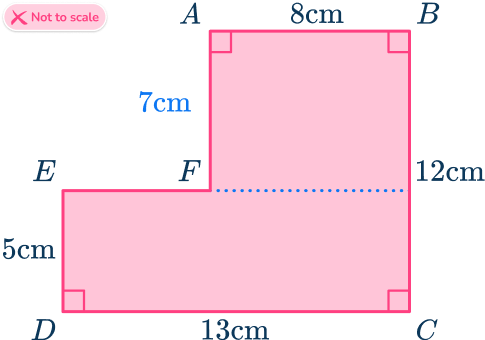
The area of the top rectangle is,
\text{Area}=8\times (12-5)=56.The area of the bottom rectangle is,
\text{Area}=5\times 13=65.3Calculate the total area of the hexagon.
The total area of the hexagon is found by adding the area of the top and bottom rectangles together.
\text{Total Area}=65+56=1214Write the answer, including the correct units.
The dimensions of the shape are given in centimeters, so the units of the area will be in square centimeters.
The area of hexagon ABCDEF is 121 \ cm^2.
Example 2: irregular hexagon with inconsistent units
Find the area of the irregular hexagon ABCDEF.
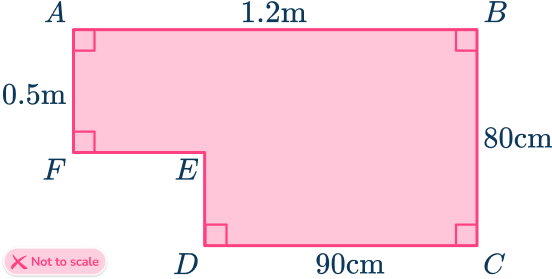
Consider the hexagon as a compound shape and split it appropriately.
You can split the ‘L’ shape into two rectangles.
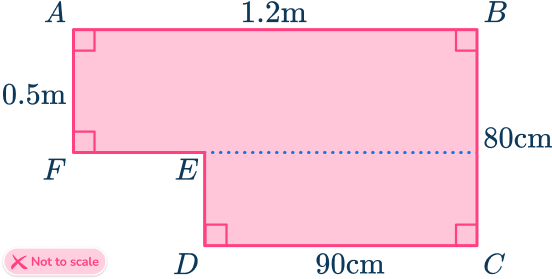
Calculate the area of the parts.
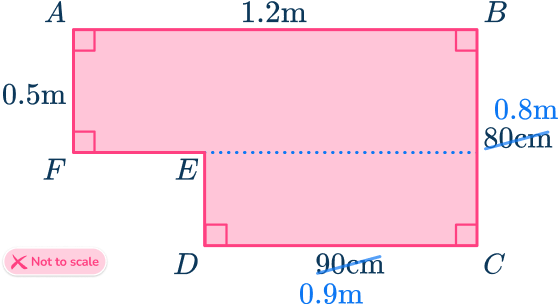
The dimensions of the top rectangle are both in meters.
The area of the top rectangle is,
\text{Area}=0.5\times 1.2=0.6.
To calculate the area of the bottom rectangle, be consistent and use meters. The area of the bottom rectangle is
\text{Area}=0.9\times (0.8-0.5)=0.27.
Calculate the total area of the hexagon.
The total area of the hexagon is found by adding the area of the two rectangles together.
\text{Total Area}=0.6+0.27=0.87
Write the answer, including the correct units.
The dimensions of the shape used to calculate the area are meters, so the units of the area will be in square meters.
The area of hexagon ABCDEF is 0.87 \ m^2 \; ( or 870 \ cm^2).
Example 3: area of a regular hexagon given the area of one of the equilateral triangles
Calculate the area of the regular hexagon ABCDEF given that the area of one of the congruent triangles is 14 \ m^2.
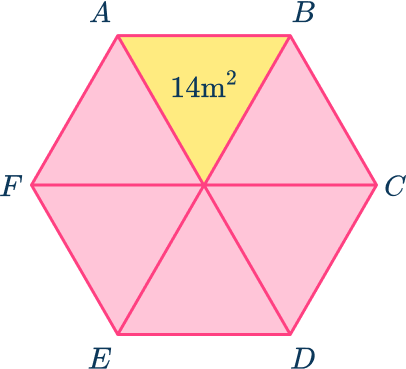
Consider the hexagon as a compound shape and split it appropriately.
The hexagon has already been split into six equilateral triangles for us.
Calculate the area of the parts.
The area of one triangle has been given in the question, 14 \ m^2.
Calculate the total area of the hexagon.
The area of the regular hexagon is,
\begin{aligned} \text{Area } & \text{ of regular hexagon} \\\\ &=6\times \text{Area of one triangle}\\\\ &=6\times 14\\\\ &=84 \end{aligned}
Write the answer, including the correct units.
The area of hexagon ABCDEF is 84 \ m^2.
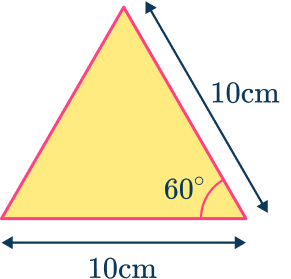
Example 4: area of a hexagon given the side length
Calculate the area of the regular hexagon ABCDEF given that the length of one side of a regular hexagon is 10 \ cm. Give your answer to 1 decimal place.
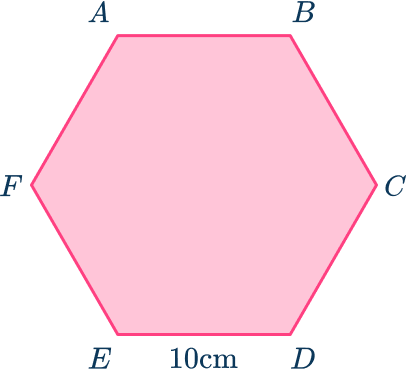
Consider the hexagon as a compound shape and split it appropriately.
Here, the regular hexagon ABCDEF has been split into six congruent equilateral triangles.
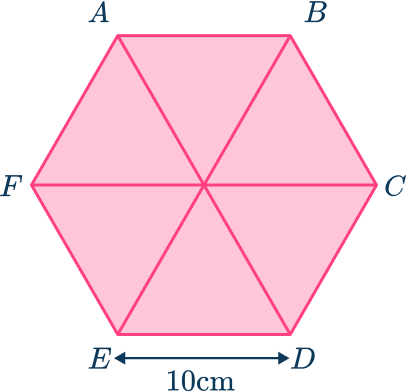
Calculate the area of the parts.
There are three methods you can use to find the area of an equilateral triangle by forming a right triangle with a right angle. The first two methods to find the height of the triangle are shown below.
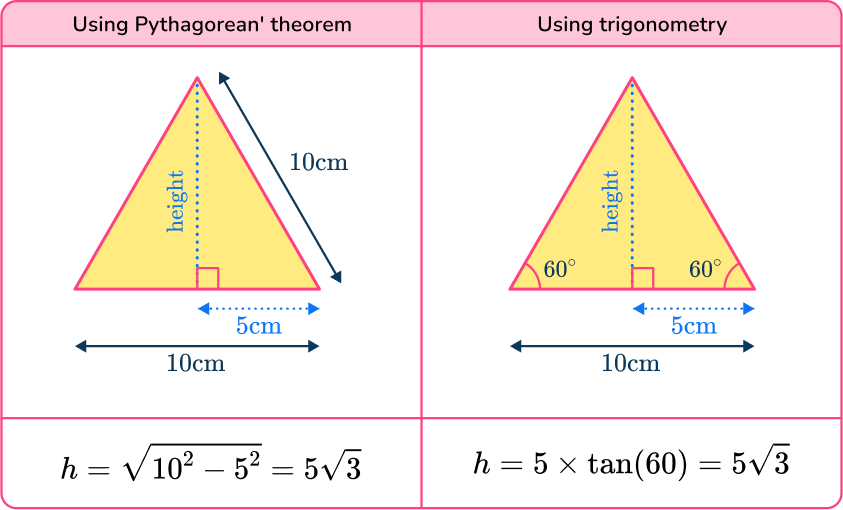
The area of one of the equilateral triangles is,
The third method uses the HIGHER trigonometry formula for the area of a triangle.
Calculate the total area of the hexagon.
The area of the regular hexagon is,
\begin{aligned} \text{Area } & \text{ of regular hexagon} \\\\ &=6\times \text{Area of one triangle}\\\\ &=6\times 25\sqrt{3}\\\\ &=150\sqrt{3} \end{aligned}
Write the answer, including the correct units.
The dimensions of the shape are given in centimeters, so the units of the area will be in square centimeters.
The area of hexagon ABCDEF is 259.8 \ cm^2 ( to 1 decimal place ).
Example 5: area of a hexagon given the height (apothem)
Calculate the area of the regular hexagon ABCDEF given that the length of the apothem of the regular hexagon is 12 \ cm. Give your answer to 1 decimal place.
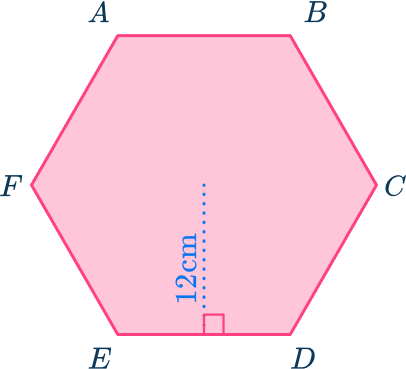
Consider the hexagon as a compound shape and split it appropriately.
Here, the regular hexagon ABCDEF has been split into six congruent equilateral triangles.
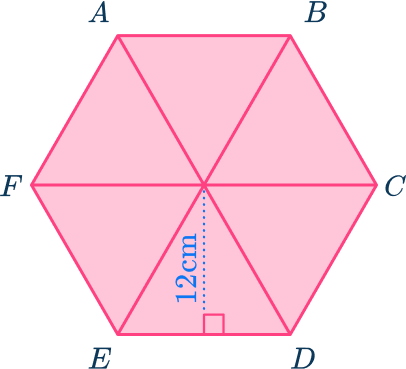
Calculate the area of the parts.
You need to work out the base of the triangle.
This can be done using trigonometry with the angles inside the equilateral triangle.
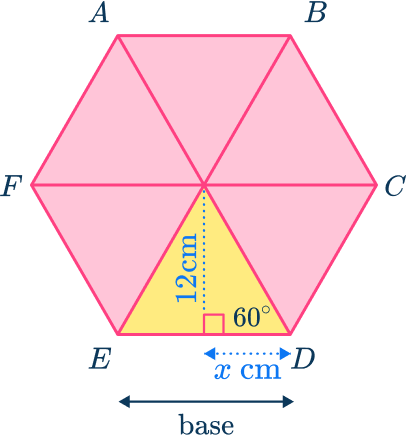
x=12\div \tan(60)=4\sqrt{3}
The base of one of the equilateral triangles is,
\text{base}=2x=2\times 4\sqrt{3}=8\sqrt{3}.
The area of one of the equilateral triangles is,
Calculate the total area of the hexagon.
The area of the regular hexagon is,
Write the answer, including the correct units.
The dimensions of the shape are given in centimeters, so the units of the area will be in square centimeters.
The area of hexagon ABCDEF is 498.8 \ cm^2 ( to 1 decimal place ).
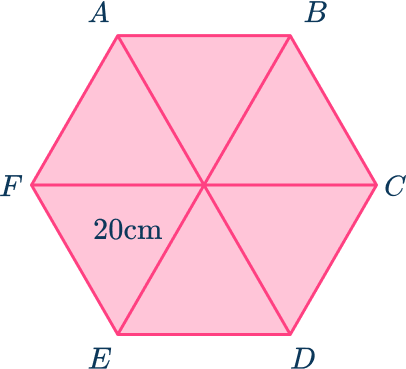
Example 6: area of a hexagon given the radius of the circumcircle
Calculate the area of the regular hexagon ABCDEF given that the length from the center of the hexagon to the vertices is 20 \ cm. Give your answer in exact form.
Consider the hexagon as a compound shape and split it appropriately.
Here, the regular hexagon ABCDEF is split into six congruent equilateral triangles.
Calculate the area of the parts.
You need to work out the height of the triangle using trigonometry with the angles inside the equilateral triangle. The hypotenuse of the triangle is 20 \ cm.
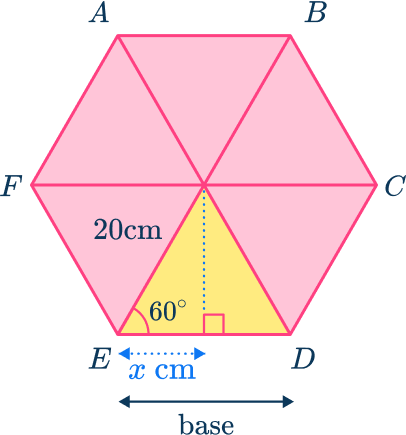
\text{height}=\sin(60)\times 20=10\sqrt{3}
You need to work out the base of the triangle using trigonometry with the angles inside the equilateral triangle. The hypotenuse of the triangle is 20 \ cm.
x=\cos(60) \times 20=10
The base of one of the equilateral triangles is,
The area of one of the equilateral triangles is,
The alternative method uses the HIGHER trigonometry formula for the area of a triangle.
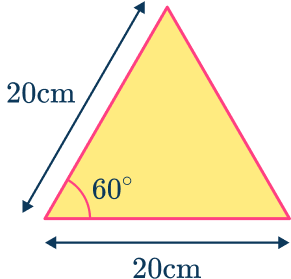
Calculate the total area of the hexagon.
The area of the regular hexagon is,
Write the answer, including the correct units.
The dimensions of the shape are given in centimeters, so the units of the area will be in square centimeters.
The area of hexagon ABCDEF is 600\sqrt{3} \ cm^2, in exact form.
Teaching tips for area of a hexagon
- Before students can find the area of a hexagon, check for understanding of basic hexagon knowledge, including what it is and real life examples of the shape, such as a honeycomb or soccer ball.
- Encourage students to use technology tools, such as an area of hexagon calculator to check their work in real time. This can assist with students not forming misconceptions as they are getting feedback quickly.
- Allow students time to practice with different examples, working independently and with other students.
Easy mistakes to make
- Using incorrect units
Remember that area is measured in square units. Square units include square centimeters (cm^2), square meters (m^2) and square millimeters (mm^2).
- Rounding answers too early
It is important to not round decimals until the end of all the calculations. Rounding too early could result in an inaccurate answer.
- Confusing the dimensions being used
It is important to make sure you keep track of which dimensions you have been given and which dimensions you are calculating. Pay attention to each step of your work and use any given diagrams as you work through the problem.
- Not providing the answer in the form requested
It is important to leave your answer in exact form if asked to. This may involve square roots ( for example, \sqrt{2}) and/or \pi.
Practice area of a hexagon questions
1. Calculate the area of the irregular hexagon ABCDEF. Give your answer in square centimeters.
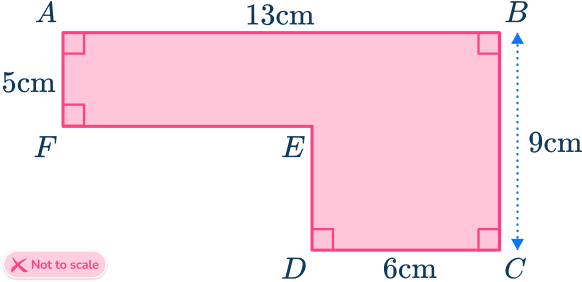




The irregular hexagon ABCDEF can be split into two rectangles.
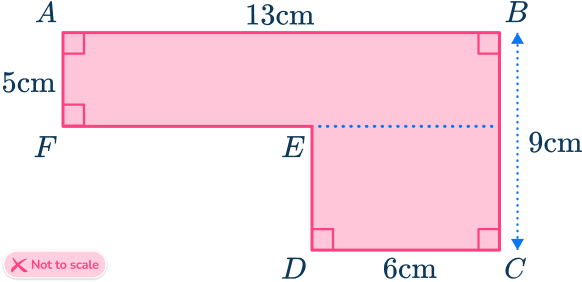
The area of the top rectangle is
\text{Area}=13\times 5=65.
The area of the bottom rectangle is
\text{Area}=6\times (9-5)=24.
The total area of the irregular hexagon is found by adding the two separate areas together.
\text{Total area}=65+24=89 \ cm^2
2. Calculate the area of the irregular hexagon ABCDEF. Give your answer in square meters.
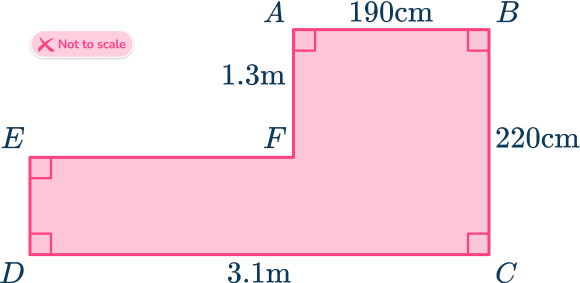




The irregular hexagon ABCDEF can be split into two rectangles.
The dimensions can also be converted into meters.
190 \ cm=1.9 \ m
220 \ cm=2.2 \ m
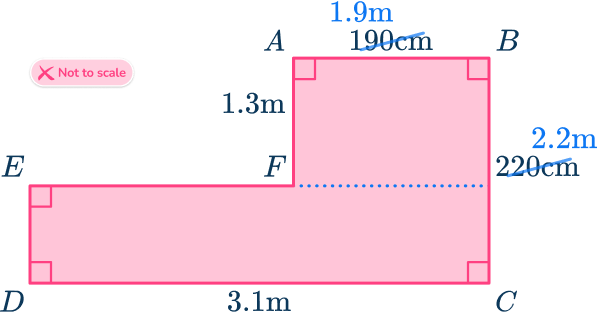
The area of the top rectangle is
\text{Area}=1.3\times 1.9=2.47.
The area of the bottom rectangle is
\text{Area}=3.1\times (2.2-1.3)=2.79.
The total area of the irregular hexagon is found by adding the two separate areas together.
\text{Total area}=2.47+2.79=5.26 \ m^2
3. Calculate the area of the irregular hexagon ABCDEF given that the area of one of the congruent triangles is 50 \ cm^2.
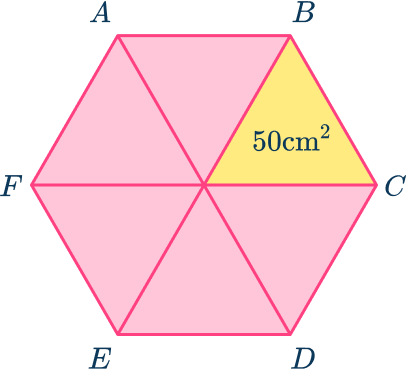




The area formula for a regular hexagon is
\begin{aligned} \text{Area } & \text{ of regular hexagon} \\\\ &=6\times \text{Area of one triangle}\\\\ &=6\times 50\\\\ &=300 \ cm^2 \end{aligned}
4. Calculate the area of the regular hexagon ABCDEF given that the length of one side of the regular hexagon is 12 \ cm.
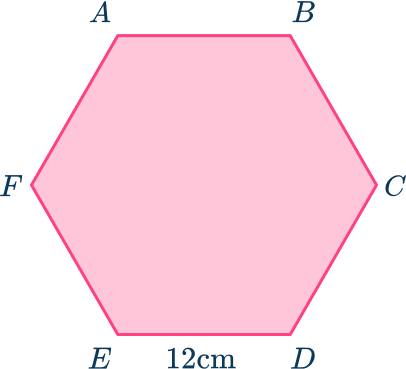




The area of a regular hexagon can be found by splitting it into 6 equilateral triangles and finding the area of one of the triangles and multiplying it by 6.
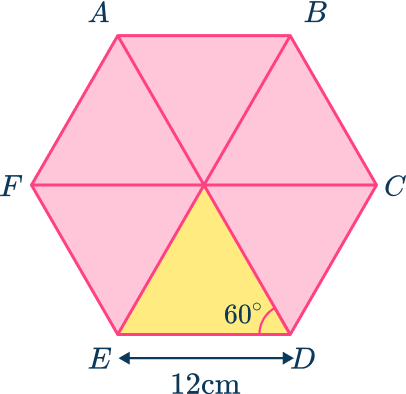
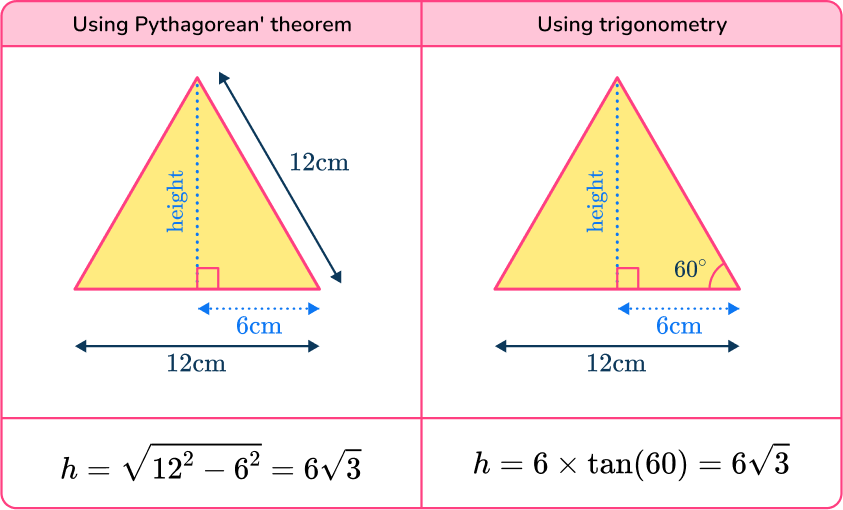
The area of one of the equilateral triangles is
\begin{aligned} A&=\cfrac{1}{2} \; bh\\\\ &=\cfrac{1}{2}\times 12\times 6\sqrt{3}\\\\ &=36\sqrt{3} \end{aligned}
The third method uses the HIGHER trigonometry formula for the area of a triangle.
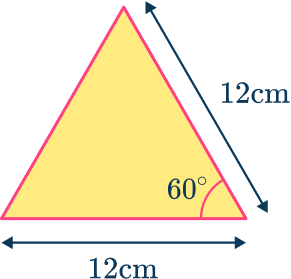
\begin{aligned} A&= \cfrac{1}{2} \; ab \sin C \\\\ &=\cfrac{1}{2} \times 12\times 12\times \sin (60)\\\\ &=36\sqrt{3} \end{aligned}
The area of the regular hexagon is
\begin{aligned} \text{Area } & \text{ of regular hexagon} \\\\ &=6\times \text{Area of one triangle}\\\\ &=6\times 36\sqrt{3}\\\\ &=216\sqrt{3}\\\\ &=374 \ cm^2 \end{aligned}
5. Calculate the area of the regular hexagon ABCDEF given that the length of the apothem of the regular hexagon is 5 \ cm.
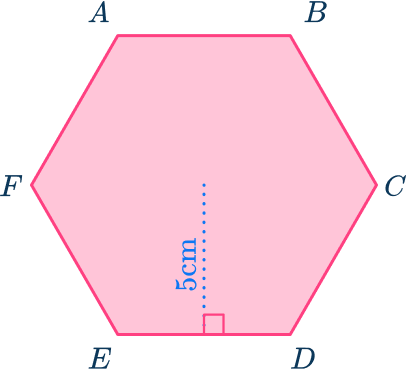




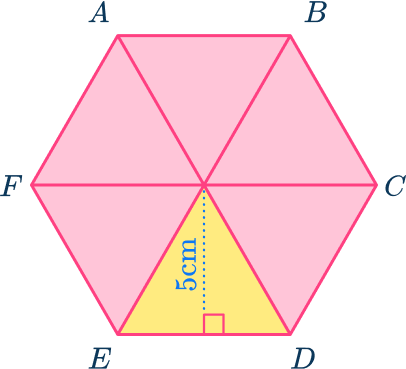
The area of a regular hexagon can be found by splitting it into 6 equilateral triangles and finding the area of one of the triangles and multiplying it by 6.
The base of the triangle is calculated using trigonometry with the angles inside the equilateral triangle.
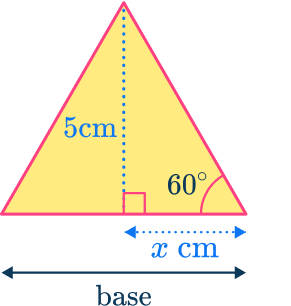
x=5\div \tan(60)=\cfrac{5\sqrt{3}}{3}
The base of one of the equilateral triangles is
\text{base}=2x=2\times \cfrac{5\sqrt{3}}{3}=\cfrac{10\sqrt{3}}{3}.
The area of one of the equilateral triangles is
\begin{aligned} A&=\cfrac{1}{2} \; bh\\\\ &=\cfrac{1}{2}\times \cfrac{10\sqrt{3}}{3}\times 5\\\\ &=\cfrac{25\sqrt{3}}{3} \end{aligned}
The area of the regular hexagon is
\begin{aligned} \text{Area } & \text{ of regular hexagon} \\\\ &=6\times \text{Area of one triangle}\\\\ &=6\times \cfrac{10\sqrt{3}}{3}\\\\ &=50\sqrt{3}\\\\ \end{aligned}
6. Calculate the area of the regular hexagon ABCDEF given that the length from the center of the hexagon to the vertices is 6 \ cm.
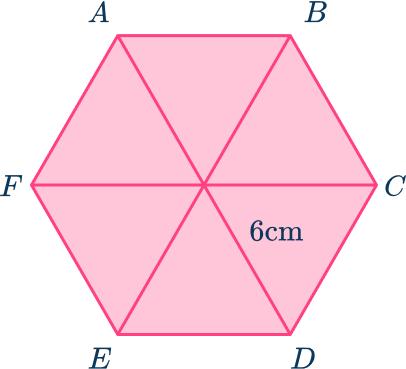




The area of a regular hexagon can be found by splitting it into 6 equilateral triangles and finding the area of one of the triangles and multiplying it by 6.
The height of the triangle can be calculated using trigonometry and the angles in the equilateral triangle.
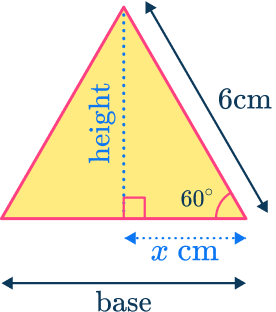
\text{height}=\sin(60)\times 6=3\sqrt{3}
The base of the triangle can be calculated using trigonometry and the angles in the equilateral triangle.
x=\cos(60) \times 6=3
The base of one of the equilateral triangles is
\text{base}=2x=2\times 3=6.
The area of one of the equilateral triangles is
\begin{aligned} A&=\cfrac{1}{2} \; bh\\\\ &=\cfrac{1}{2}\times 6\times 3\sqrt{3}\\\\ &=9\sqrt{3} \end{aligned}
The alternative method uses the HIGHER trigonometry formula for the area of a triangle.
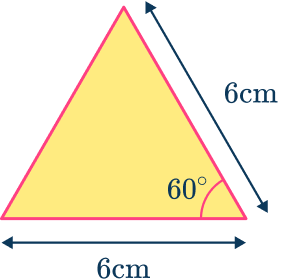
\begin{aligned} A&= \cfrac{1}{2} \; ab \sin C \\\\ &=\cfrac{1}{2} \times 6\times 6\times \sin (60)\\\\ &=9\sqrt{3} \end{aligned}
The area of the regular hexagon is
\begin{aligned} \text{Area } & \text{ of regular hexagon} \\\\ &=6\times \text{Area of one triangle}\\\\ &=6\times 9\sqrt{3}\\\\ &=54\sqrt{3} \end{aligned}
Area of a hexagon FAQs
The formula to find the area of a regular hexagon is:
\text { Area of regular hexagon }=6 \times \text { Area of one triangle }
To find the perimeter of any hexagon, you add up the length of the sides. To find the perimeter of a regular hexagon, you can simply multiply the length of the hexagon by 6.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!