15 Pythagorean Theorem Practice Problems For 8th Grade
Pythagorean Theorem practice problems involve using the relationship between the sides of a right triangle to calculate missing side lengths in triangles. The Pythagorean Theorem is introduced in 8th grade and is used to solve a variety of problems across high school.
Here, you’ll find a selection of Pythagorean Theorem questions that demonstrate the different types of questions students are likely to encounter in 8th grade.
What is the Pythagorean Theorem?
The Pythagorean Theorem is the geometric theorem that states that the square of the hypotenuse (longest side) of a right triangle is equal to the sum of the squares of the two shorter sides of the triangle.
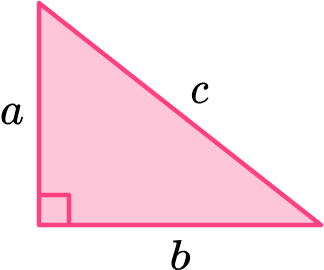
This can be written as a^2+b^2=c^2 for a triangle labeled like this:
15 Pythagoras Theorem Practice Problems
Find all of the Pythagoras Theorem questions included in this blog in this easy to download resource. Suitable for 8th grade students. Includes answer key.
Download Free Now!How to answer Pythagorean Theorem questions
1 – Label the sides of the triangle a, b, and c.
Note that the hypotenuse, the longest side of a right triangle, is opposite the right angle and will always be labeled.
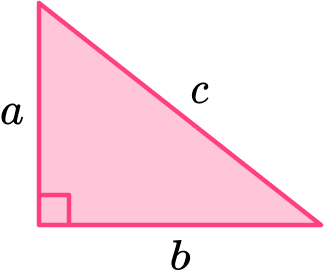
2 – Write down the formula and substitute the values>
a^2+b^2=c^23 – Calculate the answer.
You may be asked to give your answer in an exact form or round to a given degree of accuracy, such as a certain number of decimal places or significant figures.
Pythagorean Theorem in real life
Pythagorean Theorem has many real-life uses, including in architecture and construction, navigation and surveying.
Pythagorean Theorem in 8th grade
Pythagorean Theorem is usually introduced in middle school, as it is a part of the 8th grade Common Core Math Standards.
The emphasis in middle school is on students being able to:
- Explain the Pythagorean Theorem;
- Use the theorem to solve mathematical and real-world problems – with both 2D and 3D figures;
- Use the theorem to calculate the distance between two points on a coordinate grid.
The process for solving any Pythagoras Theorem problem always begins by identifying the relevant right-angled triangle and labeling the sides a, b, c. If there is not a diagram in the question, it can be helpful to draw one.
Where necessary, round your answers to 3 significant figures.
Pythagorean Theorem practice problems
1. A ship sails 6 \, km East and then 8 \, km North. Find the ship’s distance from its starting point.
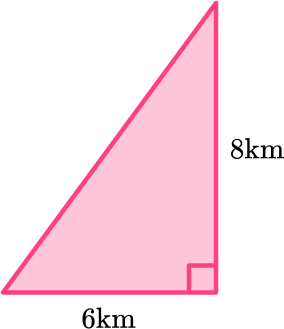
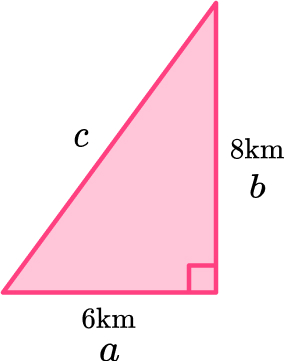
\begin{aligned} a^2+b^2&=c^2\\ 6^2+8^2&=c^2\\ 36+64&=c^2\\ 100&=c^2\\ c&=\sqrt{100}\\ c&=10 \, km \end{aligned}
The ship is 10 kilometers from its starting point.
\begin{aligned} a^2+b^2&=c^2\\ 6^2+8^2&=c^2\\ 36+64&=c^2\\ 100&=c^2\\ c&=\sqrt{100}\\ c&=10 \, km \end{aligned}The ship is 10 kilometers from its starting point.
2. A ladder is 5 \, m long. The base of the ladder is 3 \, m from the base of a vertical wall. How far up the wall does the ladder reach?
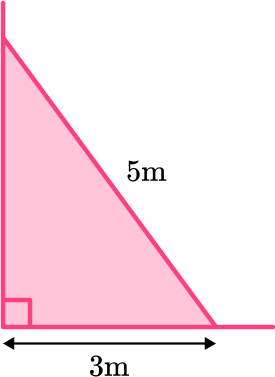
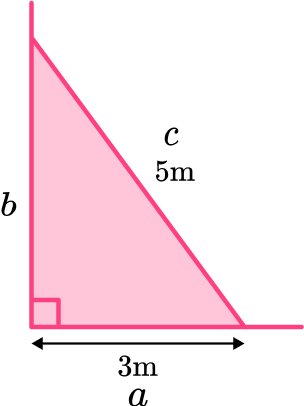
\begin{aligned} b^{2}&=c^{2}-a^{2}\\ b^{2}&=5^{2}-3^{2}\\ b^{2}&=25-9\\ b^{2}&=16\\ b&=\sqrt{16}\\ b&=4 \, m \end{aligned}
The ladder reaches 4 meters up the wall.
3. Alex and Sam start from the same point. Alex walks 400 meters west. Sam walks x meters south, until they are 600 \, m apart from each other. How far does Sam walk?
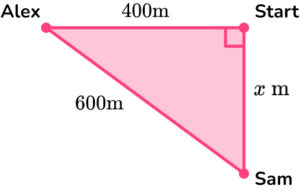
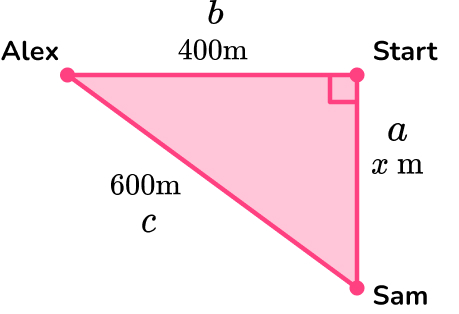
\begin{aligned} a^{2}&=c^{2}-b^{2}\\ x^{2}&=600^{2}-400^{2}\\ x^{2}&=360000-160000\\ x^{2}&=200000\\ x&=\sqrt{200000}\\ x&=447.2135955\\ x&=447 \, m ~\text{(3sf)} \end{aligned}
4. A television’s size is the measurement from the upper left hand corner of the television to the bottom right hand corner. Find the size of this television.
75 inches
150 inches
39.7 inches
55.1 inches
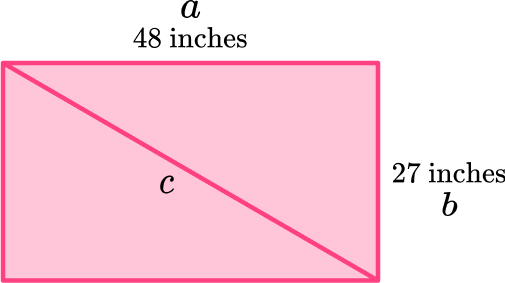
\begin{aligned} a^2+b^2&=c^2\\ 48^2+27^2&=c^2\\ 2304+729&=c^2\\ 3033&=c^2\\ c&=\sqrt{3033}\\ c&=55.07267925\\ c&=55.1 \, \mathrm{inches} ~ \text{(3sf)} \end{aligned}
5. The pole of a sailing boat is supported by a rope from the top of the pole to an anchor point on the deck. The pole is 4 \, m long and the rope is 4.5 \, m long. Calculate the distance from the base of the pole to the anchor point of the rope on the deck.
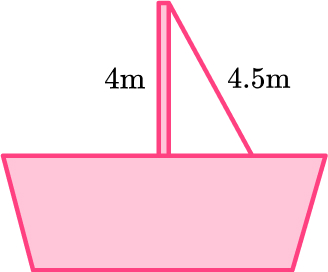
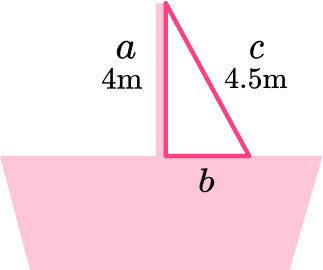
\begin{aligned} b^{2}&=c^{2}-a^{2}\\ b^{2}&=4.5^{2}-4^{2}\\ b^{2}&=20.25-16\\ b^{2}&=4.25\\ b&=\sqrt{4.25}\\ b&=2.061552813\\ b&=2.06 \, m ~\text{(3sf)} \end{aligned}
6. Work out the length of the diagonal of a square with 8 \, cm sides.
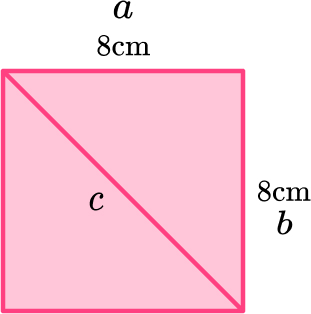
\begin{aligned} a^2+b^2&=c^2\\ 8^2+8^2&=c^2\\ 64+64&=c^2\\ 128&=c^2\\ c&=\sqrt{128}\\ c&=11.3137085\\ c&=11.3 \, cm ~ \text{(3sf)} \end{aligned}
The diagonal of the square has a length of 11.3 centimeters.
7. ABC is an isosceles triangle.
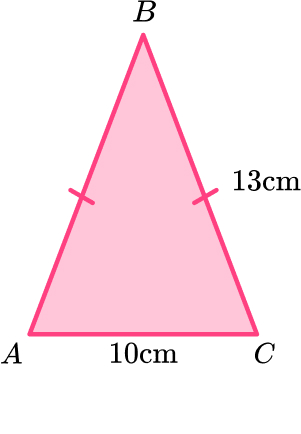
Work out the height of the triangle.
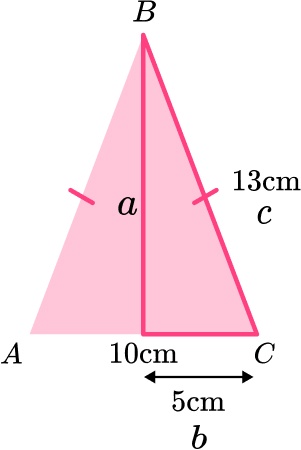
\begin{aligned} a^{2}&=c^{2}-b^{2}\\ a^{2}&=13^{2}-5^{2}\\ a^{2}&=169-25\\ a^{2}&=144\\ a&=\sqrt{144}\\ a&=12 \, cm \end{aligned}
8. ABCD is an isosceles trapezoid.
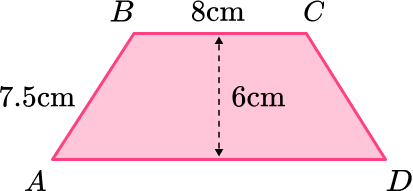
Work out the length of AD.
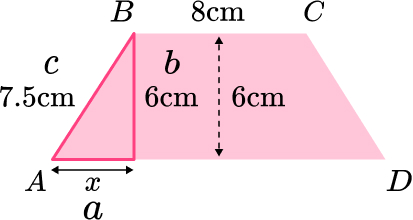
\begin{aligned} a^{2}&=c^{2}-b^{2}\\ x^{2}&=7.5^{2}-6^{2}\\ x^{2}&=56.25-36\\ x^{2}&=20.25\\ x&=\sqrt{20.25}\\ x&=4.5 \, cm \end{aligned}
AD=4.5+8+4.5=17 \, cm
9. Here is a cm square grid. Calculate the distance between the points A and B.
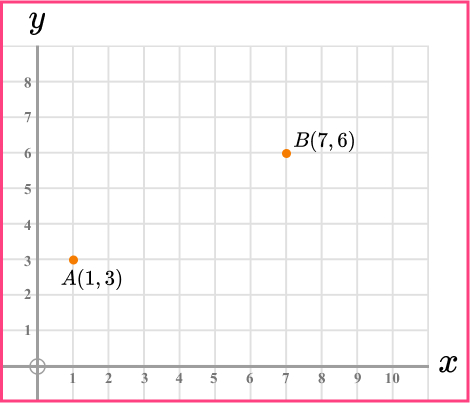
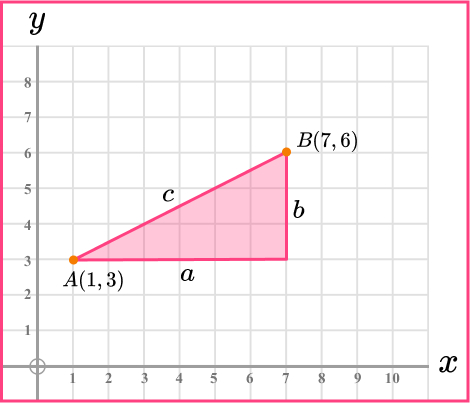
\begin{aligned} a^2+b^2&=c^2\\ 6^2+3^2&=c^2\\ 36+9&=c^2\\ 45&=c^2\\ c&=\sqrt{45}\\ c&=6.708203932\\ c&=6.7 \, cm ~ \text{(3sf)} \end{aligned}
10. Which is a right angled triangle?
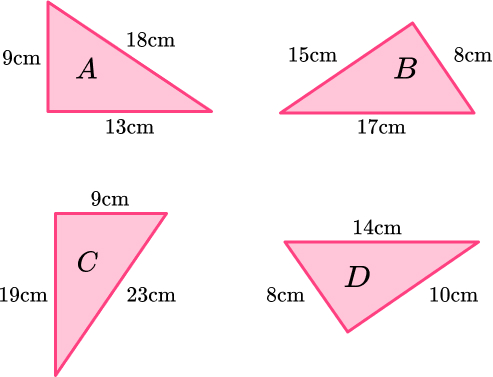
Not a right angled triangle because Pythagorean Theorem doesn’t work.
\begin{aligned} \text{B: } 8^{2}+15^{2}&=289\\ 17^{2}&=289 \\ \end{aligned}Right angled triangle because Pythagorean Theorem works.
\begin{aligned} \text{C: } 9^{2}+19^{2}&=442\\ 23^{2}&=529 \\ \end{aligned}Not a right angled triangle because Pythagorean Theorem doesn’t work.
\begin{aligned} \text{D: } 8^{2}+10^{2}&=164\\ 14^{2}&=196 \\ \end{aligned}Not a right angled triangle because Pythagorean Theorem doesn’t work.
11. PQRS is made from two right angled triangles.
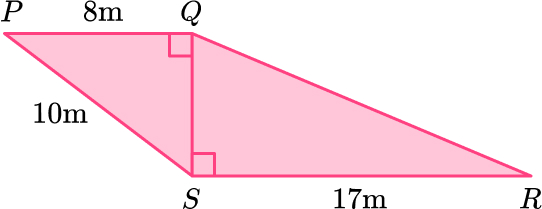
Work out the length of QR.
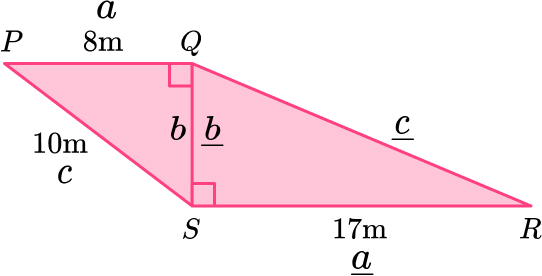
Triangle \text{PQS:}
\begin{aligned} \\ b^{2}&=c^{2}-a^{2}\\ b^{2}&=10^{2}-8^{2}\\ b^{2}&=100-64\\ b^{2}&=36\\ b&=\sqrt{36}\\ b&=6 \, m \end{aligned}Triangle \text{QRS}
\begin{aligned} \\ a^2+b^2&=c^2\\ 17^2+6^2&=c^2\\ 289+36&=c^2\\ 325&=c^2\\ c&=\sqrt{325}\\ c&=18.02775638\\ c&=18.0 \, m ~ \text{(3sf)} \end{aligned}12. Here is a pattern made from right angled triangles. Work out the length x.
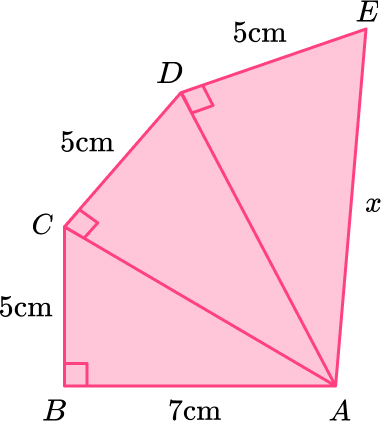
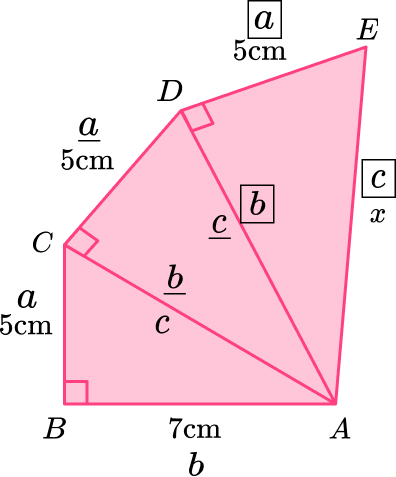
Triangle \text{ABC:}
\begin{aligned} \\ a^2+b^2&=c^2\\ 5^2+7^2&=c^2\\ 74&=c^2\\ c&=\sqrt{74}\\ c&=8.602325267 \end{aligned}
Triangle \text{ACD:}
\begin{aligned} \\ a^2+b^2&=c^2\\ 5^2+8.60232567^2&=c^2\\ 99&=c^2\\ c&=\sqrt{99}\\ c&=9.949874371 \end{aligned}13. Here is a pyramid.
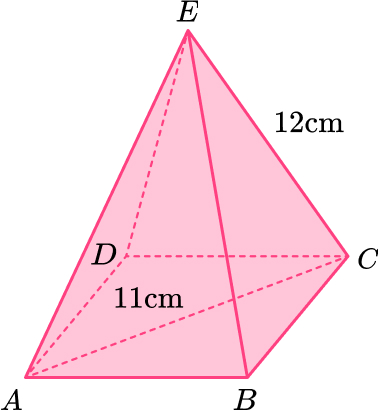
Work out the height of the pyramid.
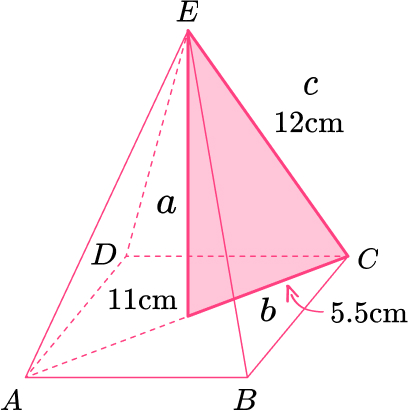
\begin{aligned} a^{2}&=c^{2}-b^{2}\\ a^{2}&=12^{2}-5.5^{2}\\ a^{2}&=113.75\\ a&=\sqrt{113.75}\\ a&=10.6653645 \mathrm{cm} \\ a&=10.7 \, cm ~ \text{(3sf)} \end{aligned}
14. Here is a cuboid.
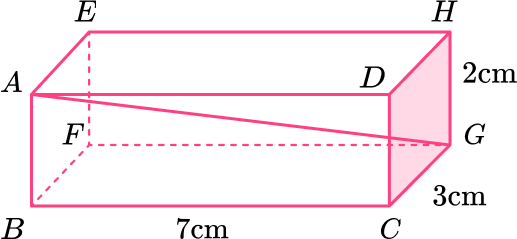
Work out the length AG.
Give your answer in its exact form.
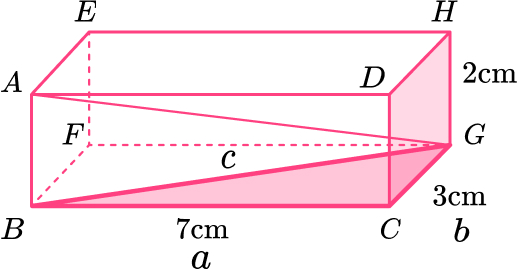
Length of \text{BG:}
\begin{aligned} \\ a^2+b^2&=c^2\\ 7^2+3^2&=c^2\\ 58&=c^2\\ c&=\sqrt{58}\\ c&=7.615773106 \end{aligned}
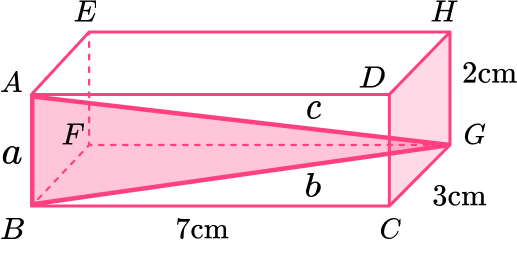
Length of \text{AG:}
\begin{aligned} \\ a^2+b^2&=c^2\\ 2^2+7.615773106^2&=c^2\\ 62&=c^2\\ c&=\sqrt{62} \, cm \end{aligned}15. Here is a right angled triangle.
Form an equation and use it to work out the value of x.
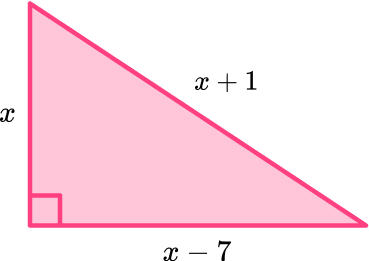
x=4 \, or \, x=12
x cannot be 4 as you can’t have a negative side length so x=12
Pythagorean Theorem in middle school
In middle school, students…
- prove the Pythagorean Theorem;
- use the Pythagorean Theorem with trigonometric ratios to solve problems;
- use the Pythagorean Theorem in proofs.
Pythagoras Theorem may feature in questions alongside other topics, such as trigonometry, circle theorems or algebra.
The Pythagorean Theorem is used to calculate a missing length in a right triangle . If you have a right angled triangle and you know two of the lengths, label the sides of the triangle a,b and c (c must be the hypotenuse – the longest side).
Pythagorean Theorem is a^2+b^2=c^2.
Substitute the values you know into Pythagorean Theorem and solve to find the missing side.
The hypotenuse of a right triangle is the longest side. If you know the lengths of the other two sides, you can find the length of the hypotenuse by squaring the two shorter sides, adding those values together and then taking the square root.
By doing this you are finding c in a^2+b^2=c^2
If your triangle is a right triangle and you know two of the sides, you can use Pythagorean Theorem to find the length of the third side. To do this, label the sides a, b and c (with c being the hypotenuse – the longest side). Substitute the values you know into a^2+b^2=c^2 and solve to find the missing side.
Looking for more Pythagorean theorem math questions?
Try these:
- Ratio questions
- Algebra questions
- Probability questions
- Trigonometry questions
- Venn diagram questions
- Long division questions
RELATED RESOURCE:
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Why not learn more about how it works?
The content in this article was originally written by former UK Secondary teacher Beki Christian and has since been revised and adapted for US schools by elementary and middle school teacher Kathleen Epperson.
