4th Grade Math Curriculum Toolkit: Lesson Guidance, Tips And Resources For Teachers

Navigating the 4th grade math curriculum can be both exhilarating and daunting. This crucial school year marks a significant transition, as students move from the foundational skills of the previous grade levels to the more complex concepts, computations and problem-solving required in upper elementary.

The 4th grade math curriculum prepares young learners for the increased rigor and independence they’ll encounter in middle school and beyond.

This blog covers the essential math skills and concepts that underpin 4th grade math, discusses common misconceptions that may arise and provides a wealth of resources and enrichment activities aligned with the 4th grade math curriculum.

4th grade math curriculum overview

The 4th grade math curriculum is designed to build upon the foundational skills students have developed in earlier grades while introducing more advanced concepts and problem-solving techniques.

Here is a summary of the key domains for the 4th-grade math curriculum, aligned with Common Core State Standards.

Operations and Algebraic Thinking

• Use the four operations with whole numbers to solve problems
• Gain familiarity with multiples and factors
• Generate and analyze patterns

Number and Operations in Base Ten

• Generalize place value understanding for multi-digit whole numbers
• Use place value understanding and properties of operations to perform multi-digit arithmetic

Number and Operations—Fractions

• Extend understanding of equivalent fractions and ordering
• Build fractions from unit fractions 
• Apply and extend previous understandings of operations on whole numbers
• Understand decimal notation for fractions, and compare decimal fractions

Measurement and Data

• Solve problems involving measurement and conversion of measurements from larger to smaller units.
• Represent and interpret data
• Geometric measurement: understand concepts of angle and measure angles

Geometry

• Draw and identify lines and angles, and classify shapes by properties of their lines and angles

Understanding the fourth grade math curriculum in greater depth

The 4th grade math curriculum, aligned with the Common Core State Standards, emphasizes the development of a solid understanding of critical mathematical concepts and skills.

It deepens their comprehension of foundational skills and prepares students for more advanced math in future grades.

Challenges of the 4th grade math curriculum

It’s not only teaching new concepts that proves challenges in 4th grade math but also addressing the common misconceptions and errors students are likely to make.

Here is the 4th grade math curriculum in more detail, including:

• Each 4th grade domain and cluster
• Common mistakes
• Strategies to help students overcome these mistakes.

All the references are to Common Core but the guidance, recommendations and resources may also apply to other state standards.

Operations and Algebraic Thinking (4.OA)

Use the four operations with whole numbers to solve problems

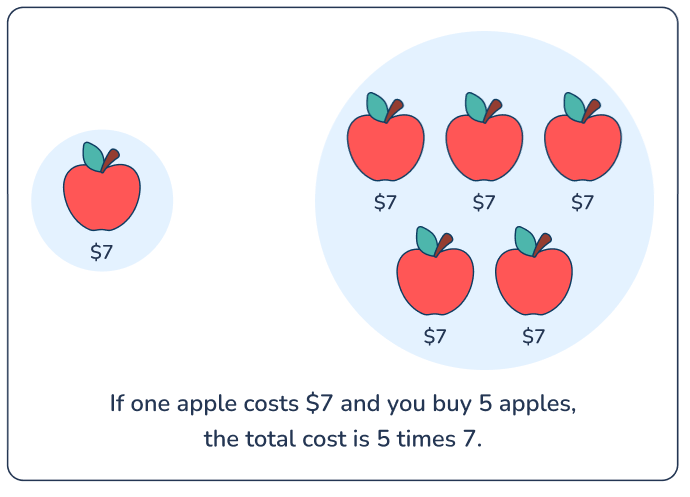
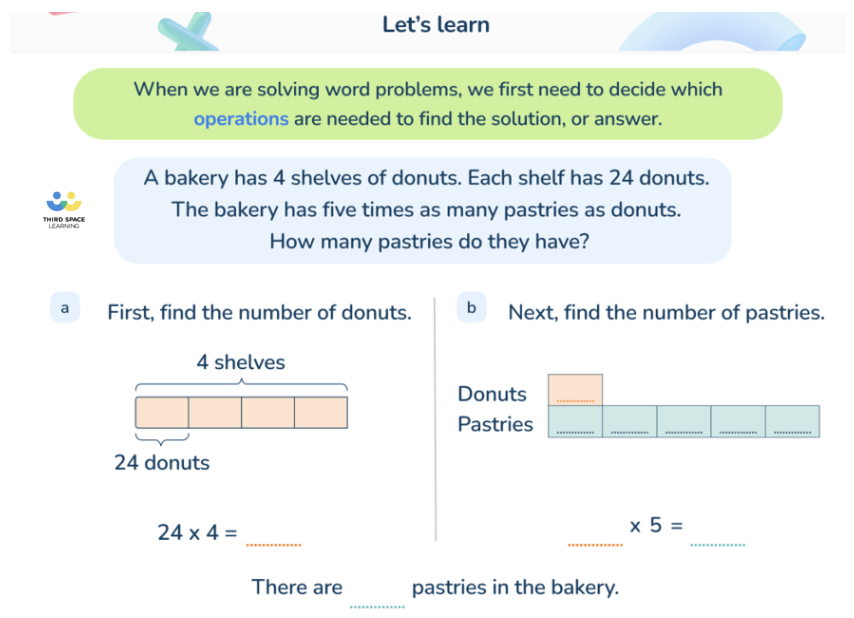
Interpret multiplication as a comparison: Students must understand that multiplication can be used to compare quantities, such as understanding that 4 times as many means multiplying by 4.

• Common mistakes: Misinterpreting the context, thinking of a multiplication equation as addition rather than a multiplicative comparison 

For example: interpreting 35 = 5 × 7 as 35 = 5 + 7.

• How to correct this: Use contextual problems and visual aids like arrays or drawings to illustrate comparisons,

For example: “If one apple costs $7 and you buy 5 apples, the total cost is 5 times 7.”

Solve multistep word problems: Students must break down a complex problem into simpler steps and apply appropriate operations in sequence.

• Common mistakes in solving multistep word problems: Missing steps or applying incorrect operations.

For example, a student adds all the numbers they see without considering the problem’s context.

• How to correct this: Teach students to break down the problem into simpler steps.

For example, use diagrams and checklists to address all parts of the problem systematically.

Gain familiarity with factors and multiples

Find factor pairs for numbers 1-100: Students should know how to identify pairs of numbers that, when multiplied together, equal the original number.

• Common mistakes in identifying factors and multiples: Students may confuse factors with multiples.

For example, listing 24 as a factor of 12.

• How to correct this: Reinforce with exercises focusing on the reciprocal nature of factors and multiples.

For example, use factor trees and Venn diagrams to segregate and understand factors and multiples visually.

Generate and analyze patterns

Create and analyze number or shape patterns: Students should be able to identify rules governing patterns and extend them accurately.

• Common mistakes in generating and analyzing patterns: Students may fail to recognize the pattern’s rule

For example, missing that the pattern increases by 3 each step.

• How to correct this: Encourage students to articulate the rule governing the pattern and validate it through multiple examples.

For example, use math manipulatives and visual aids to deliberate patterns.

Number and Operations in Base Ten (4.NBT)

Generalize place value understanding for multi-digit whole numbers

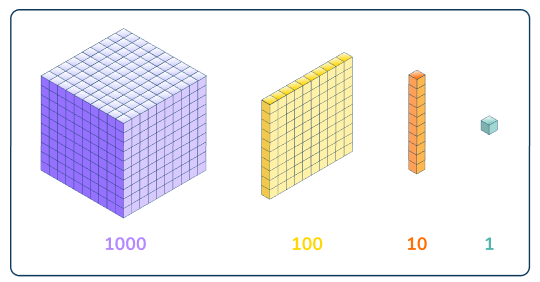
Recognize that a digit in one place represents ten times what it represents in the place to its right: Students need to comprehend the hierarchical structure of place value and its impact on the digit’s value.

• Common mistakes in understanding place value: Misplacing digits

For example, thinking in 530, the digit 3 represents 30 tens instead of 3.

• How to correct this: Practice with exercises that move digits within different place values.

For example, use a place value chart and base ten blocks to visualize the concept.

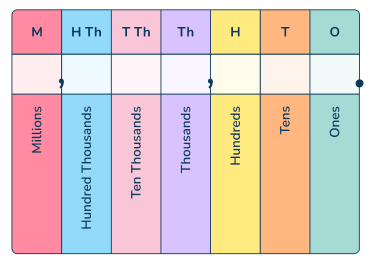
Read, write, and compare multi-digit numbers: Students should be proficient in expressing numbers in standard form, expanded form, and word form, as well as comparing their values.

• Common mistakes in reading, writing, and comparing numbers: Confusion with ordering and comparing more extensive digits.

For example, misinterpreting 5,431 as smaller than 5,143.

• How to correct this: Consistent practice with expanded, word, and standard forms.

For example, use number lines and comparative exercises to reinforce understanding of orders and magnitudes.

Use place value understanding to round multi-digit whole numbers to any place: Students should be able to apply their understanding of place value to round multi-digit whole numbers to a specified place value.

• Common mistakes in rounding multi-digit whole numbers: Incorrect identification of the target place value when rounding.

For example, rounding 456 to the nearest hundred as 500 instead of 400.

• How to correct this:  Provide real-world examples and scenarios for practical application of rounding.

For example, provide a list of snacks from the grocery store and a budget of $20. Students practice rounding to the nearest dollar to see if they have enough money for everything on the list.

Use place value understanding and properties of operations to perform multi-digit arithmetic

Fluently add and subtract multi-digit whole numbers: Students must master the standard algorithm for addition and subtraction, including regrouping and borrowing.

• Common mistakes in adding and subtracting multi-digit numbers: Errors in regrouping or borrowing.
  
• How to correct this: Step-by-step instruction with scaffolded practices

For example, utilizing lined paper to aid alignment and color-coding for different operation steps.

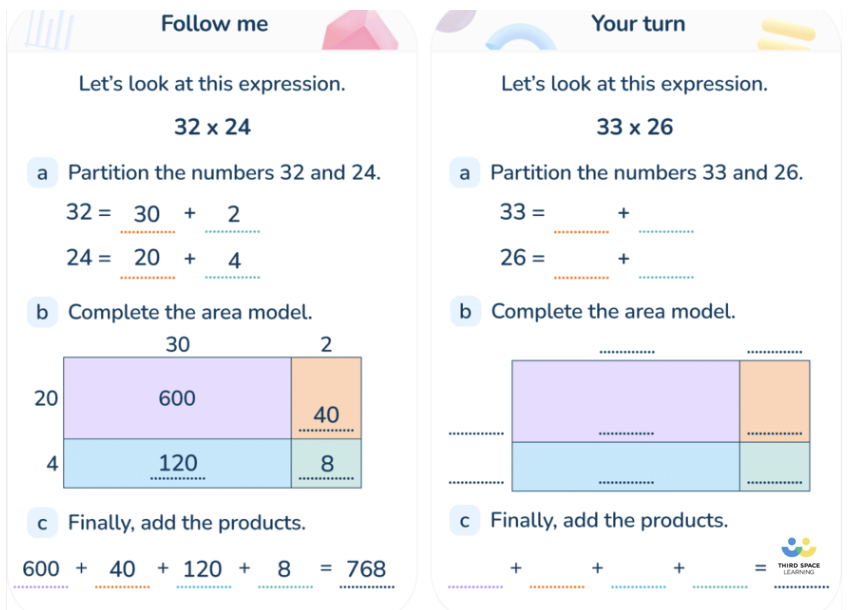
Multiply and divide multi-digit numbers: Students should be comfortable with multi-digit multiplication and understand the place value involved in these operations.

• Common mistakes in multiplying and dividing multi-digit numbers: Misalignment and misunderstanding of the division, divisors, or remainders.

For example, placing extra zeros incorrectly when multiplying.

• How to correct this: Use grid paper for alignment and visual aids, for example, arrays or area models.

Number and Operations—Fractions (4.NF)

Extend understanding of fraction equivalence and ordering

Explain why fractions are equivalent using visual fraction models: Students need to understand equivalence in fractions by visualizing that different fractions can represent the same value.

• Common mistakes in fraction equivalence: Adding the denominators along with the numerators.

For example, e.g., \frac{1}{2} + \frac{1}{4} = \frac{2}{6}.

• How to correct this: Use fractions strips and visual models to demonstrate equivalence. Emphasize the need for a common denominator in operations.

Compare fractions with different numerators and different denominators: Students should be able to find common denominators or numerators to compare the sizes of different fractions.

• Common mistakes in comparing fractions: Assuming larger numerators always mean larger values.

For example, assuming \frac{4}{10} is larger than \frac{1}{2}.

• How to correct this: Use benchmarks and encourage using visual aids like number lines or a fraction bar model.

For example, comparing fractions to \frac{1}{2}.

Build fractions from unit fractions 

Understand that a fraction \frac{a}{b} with a > 1 is a sum of fractions \frac{1}{b}: Students need to decompose fractions to see them as sums of unit fractions.

• Common mistakes in building fractions from unit fractions: Misunderstanding or treating a unit fraction as a whole number.

For example,  looking at the denominators and assuming that a larger number must mean a larger fraction.

• How to correct this: Practice decomposing fractions.

For example, use visual aids, manipulatives, and physical models to illustrate sums of unit fractions.

Add and subtract mixed numbers with like denominators: Add and subtract mixed numbers with similar denominators either converting each mixed number into an equivalent fraction or using properties of operations.

• Common mistakes in adding and subtracting mixed numbers with like denominators: Misunderstanding the relationship between mixed numbers and fractions leading to errors in calculations.
  

• How to correct this: Encourage students to first convert mixed numbers into improper fractions to simplify addition and subtraction processes.

Solve word problems involving addition and subtraction of fractions with like denominators: Fractions may pertain to the same whole and possess similar denominators. Students should employ visual fraction models and equations to represent and solve these word problems.

• Common mistakes in solving word problems involving addition and subtraction of fractions: Misinterpreting the relationship between fractions and the whole can lead to errors in problem-solving.
  

• How to correct this: Encourage the use of visual fraction models to visually represent the fractions being added or subtracted within the context of the word problem.

Apply and extend understanding of operations on whole numbers

Apply and extend previous understandings of multiplication to multiply a fraction by a whole number: Students should grasp the concept of scaling a fraction by a whole number to determine a specified fraction of the whole.

• Common mistakes: Misinterpreting the operation as simply multiplying the numerator by the whole number without adjusting the denominator.

• How to correct this: Reinforce the concept of scaling and visual representation when multiplying a fraction by a whole number. Encourage students to view the whole number as a fraction with a denominator of 1 to aid in understanding the fraction of the whole being calculated.

For example, when solving the problem \frac{2}{3} x 4, prompt students to think of the whole number 4 as \frac{4}{1} and proceed with the multiplication: (2 x 4)/(3 x 1) = \frac{8}{3}. Encourage students to simplify the resulting fraction.

Understand decimal notation for fractions, and compare decimal fractions

Express fractions with denominators 10 and 100 as decimals: Students should convert fractions with denominators of 10 or 100 into decimal form – tenths or hundredths.

• Common mistakes in decimal notation: Misplacing decimal points when converting fractions

For example, writing 0.75 as 0.075.

• How to correct this: Use decimal grids and place value charts to visualize and correctly place decimal points.

Compare decimals to hundredths: Students must compare decimal values using reasoning through place values.

• Common mistakes in comparing decimals: Confusing decimal place values.

For example, assuming 0.6 is less than 0.56 since 6 < 56.

• How to correct this: Align decimals using place value and use visual models like grids. Encourage step-by-step comparison strategies from left to right.

Measurement and Data (4.MD)

Solve problems involving measurement and conversion of measurements

Convert measurements within the same system: Students should be able to use conversion factors to change units within the same measurement system (e.g., inches to feet).

• Common mistakes in converting measurements: Inappropriate application of conversion factors. For example, addition instead of multiplication.
  
• How to correct this: Teach explicit conversion factors through consistent practice. Use real-world objects for practical understanding and visual conversion charts.

Read more: Conversion of measurement units

Apply the area and perimeter formulas for rectangles in real-world and mathematical problems: Students are expected to apply the formulas for calculating the area of a rectangle and the perimeter of a rectangle in real-world scenarios and mathematical problems.

• Common mistakes in applying the area and perimeter formulas for rectangles: Incorrectly identifying which formula to use for a given problem.

For example, students may mistakenly calculate perimeter when the question requires finding the area or vice versa.

• How to correct this: Encourage students to carefully read and analyze the problem to determine whether the question is asking for the area or the perimeter of the rectangle.

Represent and Interpret Data

Make a line plot to display a data set of measurements: Students should know how to construct and interpret a line plot accurately.

• Common mistakes in representing and interpreting data: Misreading scales or incorrectly plotting data points.
  
• How to correct this: Engage students in collecting and plotting their data. Use clear instructions on scales, ensuring comprehension and practice in accurate plotting.

Geometric measurement: understand concepts of angles and measure angles

Recognize and measure angles: Students need to understand different types of angles and use a protractor to measure them accurately.

• Common mistakes in measuring angles: Incorrect protractor placement or reading scales improperly.
  
• How to correct this: Provide hands-on protractor practice for measuring angles, including clear step-by-step placement and reading instructions. For example, allowing students to measure angles around the classroom

Recognize angle measures as additive and solve addition and subtraction problems to find unknown angles: In real-world and mathematical problems, students should apply this concept to solve addition and subtraction problems involving unknown angles on diagrams. This may involve using equations with symbols to represent the unknown angle measures for effective problem-solving.

• Common mistakes: Miscalculating the total angle measure when decomposing an angle into parts.
  
• How to correct this: Encourage students to carefully analyze the angles in the diagram and decompose them into non-overlapping parts.

Geometry (4.G)

Draw and identify lines and angles, and classify shapes by properties of their lines and angles

Draw points, lines, segments, rays, and angles: Identify and draw these geometric elements accurately.

• Common mistakes: Confusing elements like line segments and rays.
• How to correct this: Use interactive drawing exercises and visual aids to reinforce understanding. Practice distinguishing between different geometric elements using physical and digital tools.

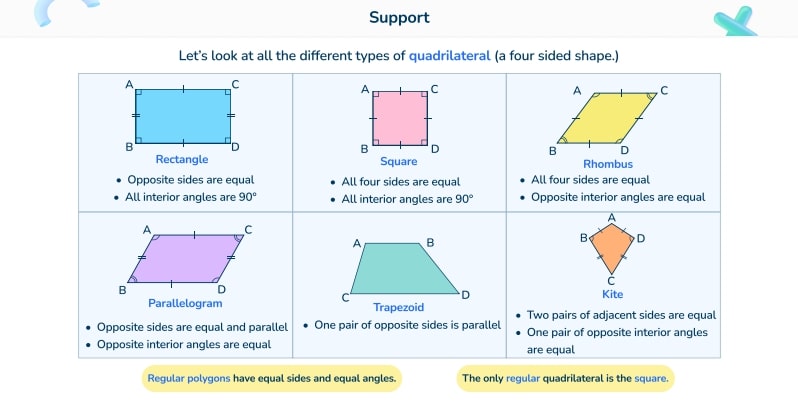
Classify shapes by properties of their lines and angles: Students should be able to distinguish and categorize shapes based on the properties of shapes, such as angles and sides.

• Common mistakes in classifying geometric shapes: Misidentifying shapes based on inadequate or incorrect properties

For example, assuming all quadrilaterals are rectangles.

• How to correct this: Encourage consistent practice to solidify understanding.

For example, having sorting activities with a variety of different shapes and practicing detailed properties

Identify lines of symmetry in two-dimensional figures: Students should know how to find and draw a line of symmetry.

• Common mistakes in recognizing symmetry: Confusing asymmetrical shapes with symmetrical ones.
  
• How to correct this: Engage students in creating symmetrical designs to reinforce their comprehension.

For example, use foldable shapes and mirrors to explore visual symmetry.

Teaching problem-solving in 4th grade math

Problem-solving in the 4th-grade math curriculum encourages persistence and the ability to analyze and articulate reasoning.  

Integrating problem-solving into daily math lessons promotes resilience and encourages students to think critically and creatively.

Here are some tips and strategies for teaching 4th grade word problems and problem-solving, aligned with the 4th grade Common Core math curriculum:

1. Make sense of problems and persevere in solving them

Encourage students to read mathematical problems carefully and underline key information.

Teach them to break down the problem into smaller, more manageable parts to identify what is being asked.

• Use a “Think-Aloud” strategy: Solve problems out loud to model your thought process, helping students visualize how to approach problems methodically.
• Implement a “Problem of the Day” routine: Introduce a new problem each day, gradually increasing in complexity.

Encourage persistence and reward effort and strategies rather than just correct answers.

2. Reason abstractly and quantitatively

Help students connect mathematical symbols to quantities and real-world objects. It can help to use visual aids and manipulatives to represent problems abstractly.

• Use visual aids: Encourage students to use drawings, charts, and manipulatives, such as base-ten blocks, to visualize problems.
• Promote estimation: Before calculating exact answers, have students estimate outcomes to develop number sense and quantitative reasoning.

3. Construct viable arguments and critique the reasoning of others

Create a classroom environment where students feel comfortable explaining their reasoning and thought processes to peers.

• Encourage a discussion-rich environment: Have students engage in respectful discussion and explain their problem-solving strategies and reasoning to their classmates.
• Use partner work: Pair students to solve problems and constructively critique each other’s solutions.

4. Model with mathematics

Incorporate real-world scenarios and applications into math problems to help students see the relevance of mathematics in everyday life.

• Use real-world applications: Integrate problems based on real-life situations students can relate to, such as planning a school event or measuring ingredients for a recipe.
• Employ visual models: Encourage students to create and interpret visual models such as graphs, tables, and diagrams.

5. Use appropriate tools strategically

Introduce various mathematical tools and teach students how to select and use them effectively. Provide opportunities for hands-on practice in different problem-solving contexts.

• Introduce various tools: Teach students to use rulers, protractors and calculators so they can independently choose the most effective strategy.
• Tool selection discussions: Engage students in conversations about which tools are best suited for different problems and why.

6. Attend to precision

Emphasize the importance of precise calculations, clear notations, and thorough explanations. Encourage students to double-check their work for accuracy and logic.

• Highlight precision and accuracy: Stress the need for accurate calculations and explanations in math problems. A lack of precision can lead to unnecessary errors.
• Double-check work: Encourage students to review their solutions to ensure all steps are correct and logical.

7. Look for and make use of structure

Help students recognize patterns and mathematical structures to simplify problem-solving.

Teach the properties and operations that can be used to decompose complex problems.

• Identify patterns and structures: Encourage students to look for patterns in numbers and operations.
• Teach operation properties: Reinforce understanding of properties like the commutative property, associative property, and distributive property to consolidate problem-solving.

8. Look for and express regularity in repeated reasoning

Encourage students to reflect on their problem-solving strategies and identify patterns or regularities.

• Reflect on strategies: Use questioning to get students to reflect on their strategies to solve problems.
• Solve related problems: Provide sets of related problems to highlight regularities and deepen understanding of repeated reasoning.

Hands-on activities for 4th grade math

Hands-on activities allow students to deepen their understanding of mathematical concepts through engaging and hands-on experiences.

Here’s a selection of creative and effective hands-on activities to add to your lesson plans that allow students to apply math to real-world contexts.

Operations and Algebraic Thinking (4.OA)

Factor Bingo – Identifying factors and multiples

• Create Bingo cards filled with numbers between 1 and 100.
• Call out a number, and students mark the factors or multiples of that number.
• The first to get five in a row wins.

This game reinforces understanding of factors and multiples.

Number and Operations in Base Ten (4.NBT)

Decimal Diner – Performing operations with multi-digit numbers

• Students create menus with prices for food and drinks.
• They then add, subtract, and multiply to calculate total costs and change.

The game simulates real-life dining scenarios and reinforces their arithmetic skills.

Number and Operations—Fractions (4.NF)

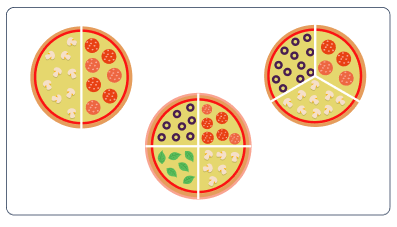
Fraction Pizzas – Understanding and building fractions

• Create a pizza party activity where students design their own pizzas using fraction pieces.
• Provide paper circles (pizza bases) and fraction pieces representing different toppings (e.g., pepperoni, mushrooms, cheese).
• Students can create pizzas based on fraction orders, such as “half pepperoni and one-fourth mushrooms.”

Students can understand equivalent fractions and the addition of fractions through this activity.

Measurement and Data (4.MD)

Angle Hunt – Measuring angles

• Set up an angle hunt around the classroom
• Students use protractors to measure angles of various objects and record their measurements.

This helps students practice using protractors and understanding angle sizes.

Geometry (4.G)

Symmetry Art – Recognizing lines of symmetry

• Students create symmetrical art projects by folding paper and cutting out shapes.
• They then unfold the shape to see the symmetrical result.

Creative tasks help students recognize and create lines of symmetry in a fun and artistic way.

Why we love teaching the 4th grade math curriculum

Fourth graders are growing in independence. They are moving away from the foundational grasp of numbers in 3rd grade and stepping into the complexities of multi-step problems and fractions.

4th grade students can handle larger numbers and more sophisticated operations but some may still benefit from visual aids and hands-on math manipulatives.

At this stage, students begin to see the logic behind math, connect ideas, and apply their knowledge creatively. Developmentally, learners are eager to explore independently but still appreciate structure and guidance.

As a 4th grade math teacher, never underestimate the power of storytelling in math problems, the effectiveness of hands-on activities, and the importance of celebrating small victories.

How Third Space Learning can help students with the 4th Grade math curriculum

In your 4th grade class, you likely have students at different stages of math development, working at various grade levels, with some needing more targeted support.

Third Space Learning offers evidence-based high-dosage tutoring for math that is personalized, one-on-one and designed to help 4th grade students at different stages in their math progress.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?