FREE DOWNLOAD
Squares Cubes And Roots Worksheet
Help your students prepare for their Maths GCSE with this free Squares, Cubes, And Roots Worksheet of 44 questions and answers
- Section 1 of the index notation, squares and cubes worksheet contains 36 skills based index notation, squares and cubes questions, in 3 groups to support differentiation
- Section 2 contains 4 applied index notation, squares and cubes with a mix of worded problems and deeper problem solving questions
- Section 3 contains 4 foundation and higher level GCSE exam style index notation, squares and cubes questions
- Answers and a mark scheme for all 44 questions
- Follows variation theory with plenty of opportunities for students to work independently at their own level
- All questions created by fully qualified expert secondary maths teachers
- Suitable for GCSE maths revision for AQA, OCR and Edexcel exam boards
Unlock access to download your free resource
You can unsubscribe at any time (each email we send will contain an easy way to unsubscribe). To find out more about how we use your data, see our privacy policy.
Raise maths attainment across your school with hundreds of flexible and easy to use GCSE maths worksheets and lessons designed by teachers for teachers.
Squares, cubes, and roots at a glance
A square number, or perfect square, is the result when an integer is multiplied by itself. For example, 9 is a square number because 3×3=9. The square root of a number is the number that has been multiplied by itself to get that number. For example the square root of 9 is 3. This is called a perfect square root since it is a whole number. We can find the square root of any number but if the number is not a perfect square then its square root will be a decimal.
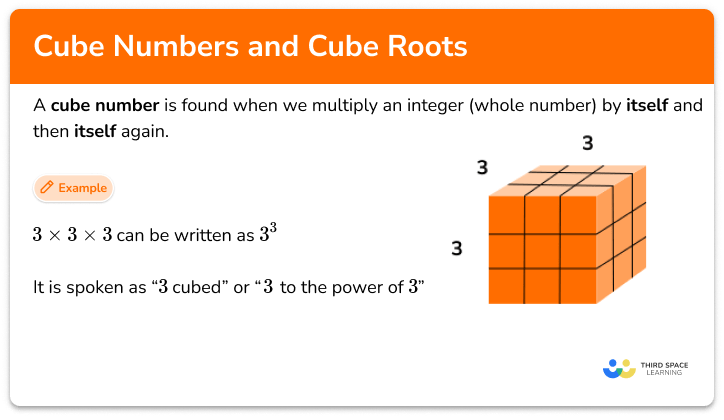
A cube number, or perfect cube, is the result when an integer is multiplied by itself three times. For example, 5x5x5=125 so 125 is a cube number. The cube root of a number is the number that has been multiplied by itself three times to get that number. For example the cube root of 125 is 5.
Square numbers and cube numbers are an important part of the number system and it is important that we can recognise the most common ones.
As well as being able to calculate squares of numbers, cubes of numbers, square roots and cube roots, we need to be able to simplify expressions involving exponents. When simplifying an expression involving indices, we don’t actually work out the calculation, but rather write it in as simple a format as possible. There are some key rules that we use when simplifying expressions involving indices:
- When multiplying terms, add the powers e.g. 3432=36
- When dividing terms, subtract the powers e.g. 5753=54
- When raising a term to another power, multiply the powers e.g. (24)3=212
These rules work only when the base number is equal and it is important to notice that the base number does not change.
Looking forward, students can then progress to additional number worksheets, for example a fractions worksheet or a rounding worksheet.
For more teaching and learning support on Number our GCSE maths lessons provide step by step support for all GCSE maths concepts.
Do you have students who need additional support?
With Third Space Learning's secondary maths tutoring programmes, students in Year 7-11 receive regular one to one maths tutoring to address gaps, build confidence and boost progress.
"My confidence in the tutoring is high. We've had some phenomenal results. I even had one girl get a Grade 8 this year; she came to every tutoring session."
Stacey Atkins, Maths Director, Outwood Grange Academies Trust