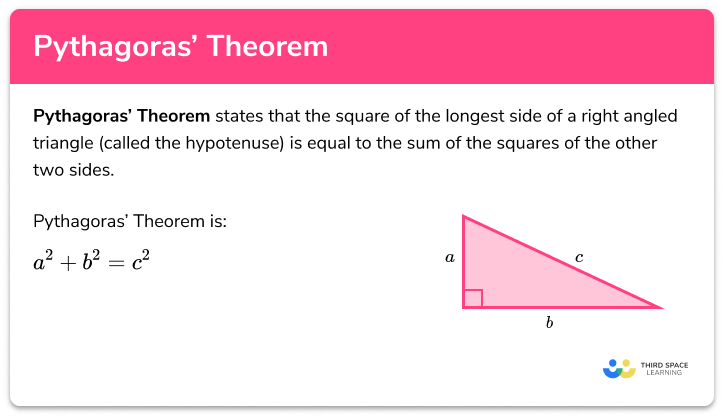
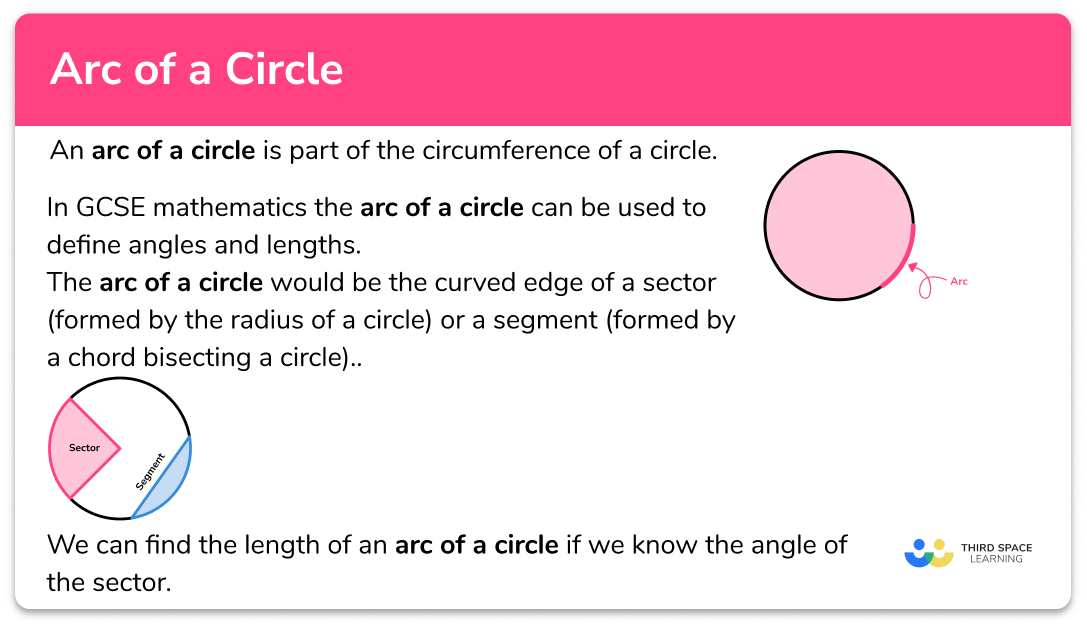
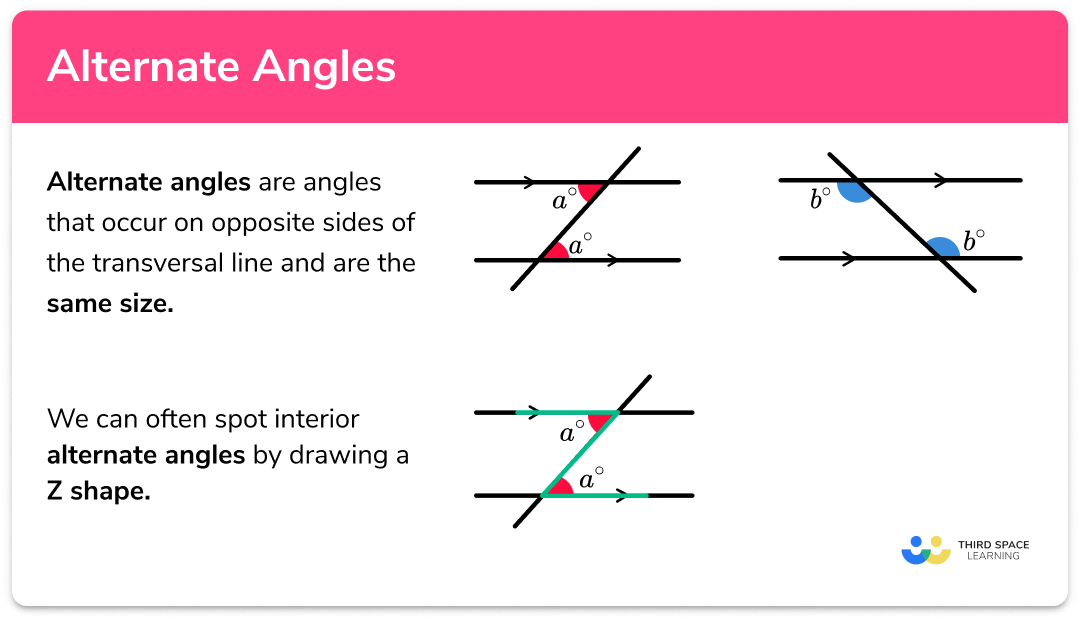
FREE DOWNLOAD
Angles In Polygons Worksheet
Help your students prepare for their Maths GCSE with this free angles in polygons worksheet of 35 questions and answers
- Section 1 of the angles in polygons worksheet contains 32 skills-based angles in polygons questions, in 2 groups to support differentiation
- Section 2 contains 3 applied angles in polygons questions with a mix of worded problems and deeper problem solving questions
- Answers and a mark scheme for all angles in polygons questions are provided
- Questions follow variation theory with plenty of opportunities for students to work independently at their own level
- All questions created by fully qualified expert secondary maths teachers
- Suitable for GCSE maths revision for AQA, OCR and Edexcel exam boards
Unlock access to download your free resource
You can unsubscribe at any time (each email we send will contain an easy way to unsubscribe). To find out more about how we use your data, see our privacy policy.
Angles in polygons at a glance
A polygon is a closed 2D shape with straight sides. A regular polygon is a polygon with all sides and all angles equal, if this is not the case it is called an irregular polygon. For example, an equilateral triangle has three equal sides and three equal angles of 60°, so it is therefore a regular polygon. Whereas an isosceles triangle only has two equal sides and angles, so is an irregular polygon.
There are several angles facts for regular and irregular polygons that are useful to know before learning about this topic. These include the fact that angles in a triangle sum to 180° and angles in a quadrilateral sum to 360°. These angle facts can then be used to work out the interior angles of any polygon, including pentagons, octagons and nonagons.
To calculate the interior angles of polygons, we divide the polygon into triangles from one vertex. The number of triangles is always two less than the number of sides of the polygon – for example, a heptagon has seven sides, and can be split into five triangles. As angles in a triangle sum to 180°, the sum of the interior angles in a heptagon must be 5180° =900°.
To find an interior angle of a regular polygon, we divide the sum of the interior angles by the total by the number of angles. For example, a hexagon can be split into four triangles, and 4180 =720°. To find an interior angle of a regular hexagon, we divide 720° by the number of sides (6), to work out that the size of each interior angle must be 120°.
The sum of the exterior angles of any polygon is 360°. If a single interior angle is known, we can calculate the size of the corresponding exterior angle by subtracting the interior angle from 180° . This is because the interior and exterior angles form a straight line.
The exterior angle of a regular polygon can be found by dividing 360° by the number of angles (or the number of sides). For example, for a regular octagon, 360 8=45°, so the size of each exterior angle is 45°. Once we have calculated an exterior angle, the interior angle can be calculated by subtracting it from 180° , in the case of the example this is 180-45=135°.
Looking forward, students can then progress to additional angles in polygons worksheets and other geometry worksheets, for example an angles in polygons worksheet or area of a triangle worksheet.

For more teaching and learning support on Geometry our GCSE maths lessons provide step by step support for all GCSE maths concepts.
Do you have students who need additional support to achieve their target GCSE maths grade?
There will be students in your class who require individual attention to help them succeed in their maths GCSEs. In a class of 30, it’s not always easy to provide.
Help your students feel confident with exam-style questions and the strategies they’ll need to answer them correctly with personalised online one to one tutoring from Third Space Learning
Lessons are selected to provide support where each student needs it most, and specially-trained GCSE maths tutors adapt the pitch and pace of each lesson. This ensures a personalised revision programme that raises grades and boosts confidence.