Inverse proportion

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Multiplying and dividing fractions Multiplying and dividing decimals Inverse functions

This topic is relevant for:

GCSE Maths Ratio and Proportion Proportion

Inverse Proportion

Here we will learn about inverse proportion, including what inverse proportion is and how to solve inverse proportion problems including real-life problem solving. We will also have a look at the inverse proportionality formula.

There are also inverse proportion worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is inverse proportion?

Inverse proportion is a type of proportionality relationship. If two quantities are inversely proportional then as one quantity increases, the other decreases.

An example of inverse proportion would be the hours of work required to build a wall. If there are more people building the same wall, the time taken to build the wall reduces.

Conversely, an example of direct proportion would be that the area of a circle is directly proportional to its radius.

Inverse proportion is also known as indirect proportion or inverse variation.

Inverse proportion is applied to real life problems such as the speed of a moving object, determining whether an item will float or sink in water, or the time taken to complete a finite task whereas direct proportion is useful in numerous real life situations such as exchange rates, conversion between units, and fuel prices.

To determine the value of a variable that is inversely proportional to another, we need to determine the relationship between the two variables and then use this to find our unknown value.

Similar to a directly proportional relationship, we need to determine the constant of proportionality, $k.$

Step-by-step guide: Direct proportion

What is inverse proportion?

Inverse proportion formula

The symbol $\propto$ is the proportionality symbol and it represents a proportional relationship between two variables. If it is inversely proportional to $x,$ we write this relationship as $y\propto\frac{1}{x}.$

This relationship can be described using an equivalence relationship. When $y$ is inversely proportional to $x$ , the value of $x \times y$ is a constant value. This value is the constant of proportionality and we use the letter $k$ to denote this value. Using a formula, we have $k=xy.$

Rearranging this formula to make $y$ the subject, we obtain the inverse proportion formula,

$y=\frac{k}{x}$ .

Step-by-step guide: Inverse proportion formula

Graphs representing an inverse proportion between two variables

Proportional relationships can also be represented by graphs. If we sketched a graph of the line $y=\frac{k}{x},$ as $x$ increases in size, $k$ is being divided by a larger number and so the result is a value $y$ that gets increasingly smaller. This gives us the curved line graph of the reciprocal function.

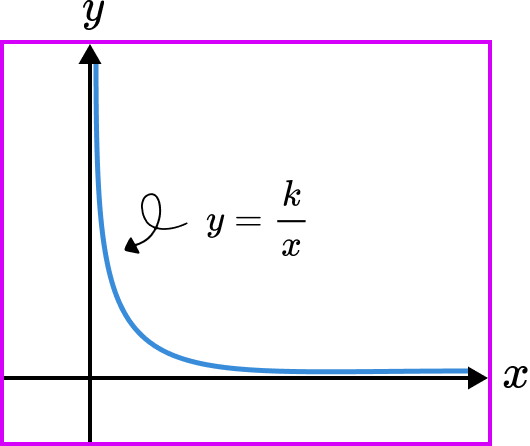
Note, the value of $y$ can be inversely proportional to other powers of $x$ including $x^{2}, \ x^{3},$ or even $\sqrt{x}.$ Each of these has a different algebraic and graphical representation.

Step-by-step guide: Directly proportional graphs / inversely proportional graphs

How to use inverse proportion

In order to work out an unknown value given an inversely proportional relationship:

Write down the inverse proportion formula.
Determine the value of $\textbf{k}$ .
Substitute $\textbf{k}$ and the known value into the inverse proportion formula.
Solve the equation.

Explain how to use inverse proportion

Inverse proportion worksheet

Get your free inverse proportion worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Inverse proportion worksheet

Get your free inverse proportion worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Inverse proportion examples

Example 1: complete the table y ∝ ⅟_x

Given that $y$ is inversely proportional to $x,$ calculate the missing value of $y$ in the table below.

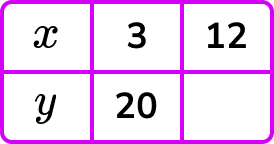
Write down the inverse proportion formula.

As $y\propto\frac{1}{x},$ we can write the formula $y=\frac{k}{x}.$

2Determine the value of $\textbf{k}$ .

Substituting a known pair of values $(3,20),$ we can say,

\begin{aligned} 20&=\frac{k}{3}\\\\ 20\times{3}&=k\\\\ k&=60 \end{aligned}

3Substitute $\textbf{k}$ and the known value into the inverse proportion formula.

Now we have the equation $y=\frac{60}{x}.$ Substituting $x=12$ into the equation to calculate the value for $y,$ we have

$y=\frac{60}{12}$ .

4Solve the equation.

Dividing $60$ by $12,$ we have $y=5.$

Notice that as the value for $x$ increased, the value for $y$ decreased.

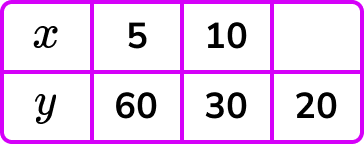
Example 2: complete the table y ∝ ⅟_x

Let $y\propto\frac{1}{x}.$ Calculate the value for $x$ when $y=20.$

Write down the inverse proportion formula.

As $y\propto\frac{1}{x}$ as stated in the question, we have

$y=\frac{k}{x}$ .

Determine the value of $\textbf{k}$ .

As $x=5$ when $y=60,$ substituting these values into the formula, we get

$\begin{aligned} 60&=\frac{k}{5}\\\\ 60\times{5}&=k\\\\ k&=300 \end{aligned}$

Substitute $\textbf{k}$ and the known value into the inverse proportion formula.

Now we have $y=\frac{300}{x}.$ We need to determine the value for $x$ when $y=20$ and so, substituting this value into the equation, we get

$20=\frac{300}{x}$ .

Solve the equation.

\begin{aligned} 20\times{x}&=300\\\\ 300\div{20}&=x\\\\ x&=15 \end{aligned}

Example 3: complete the table y ∝ ⅟_x²

Let $y$ be inversely proportional to $x^{2}.$ Calculate the missing value $q.$

Write down the inverse proportion formula.

As $y\propto\frac{1}{x^{2}},$ we have the formula $y=\frac{k}{x^{2}}.$

Determine the value of $\textbf{k}$ .

Using the table, we know that $y=4$ when $x=2.$

Note, we could also use the pair of values $y=16$ when $x=1.$

As $y=\frac{k}{x^{2}},$ substituting the values for $y=4$ and $x=2,$ we have

$\begin{aligned} 4&=\frac{k}{2^{2}}\\\\ 4&=\frac{k}{4}\\\\ 4\times{4}&=k\\\\ k&=16 \end{aligned}$

Substitute $\textbf{k}$ and the known value into the inverse proportion formula.

Now we have $y=\frac{16}{x^{2}}.$ We need to determine the value of $y=q$ when $x=4$ and so, substituting these into the equation, we have

$q=\frac{16}{4^{2}}$ .

Solve the equation.

q=\frac{16}{16}=1

Example 4: inverse proportion worded problem y ∝ ⅟_x

$2$ workers paint a fence in $9$ hours.

How long would it take $6$ workers to paint the same fence?

Write down the inverse proportion formula.

As the number of workers $x$ increases, the time $y$ taken to paint the same fence would decrease and so this is an inverse proportion of the form $y\propto\frac{1}{x}.$

This means that we have the formula $y=\frac{k}{x}.$

Determine the value of $\textbf{k}$ .

As we know $x=2$ when $y=9,$ substituting these values into the formula, we get

$\begin{aligned} 9&=\frac{k}{2}\\\\ 9\times{2}&=k\\\\ k&=18 \end{aligned}$

Substitute $\textbf{k}$ and the known value into the inverse proportion formula.

Now we have the equation $y=\frac{18}{x}.$ As we want to know the value for $y$ when $x=6,$ we substitute $x=6$ into the equation to get

$y=\frac{18}{6}$ .

Solve the equation.

As $18$ divided by $6$ is equal to $3,$ we have the solution $y=3.$

Example 5: inverse proportion worded problem y ∝ ⅟_x²

Let $n$ represent the number of dogs and $d$ represent the number of days. A bag of biscuits feeds $4$ dogs for $12$ days. Given that $d\propto\frac{1}{n^{2}},$ how many days would the same bag feed $5$ dogs?

Write down the inverse proportion formula.

As $d\propto\frac{1}{n^{2}}$ , we can state the inverse proportion formula,

$d=\frac{k}{n^{2}}.$

Determine the value of $\textbf{k}$ .

As $d=12$ when $n=4,$ substituting these into the formula, we have

$\begin{aligned} 12&=\frac{k}{4^{2}}\\\\ 12&=\frac{k}{16}\\\\ 12\times{16}&=k\\\\ k&=192 \end{aligned}$

Substitute $\textbf{k}$ and the known value into the inverse proportion formula.

Now $d=\frac{192}{n^{2}}.$ Now we have $5$ dogs, we can substitute $n=5$ into the formula to calculate the number of days of food they have,

$d=\frac{192}{5^{2}}$ .

Solve the equation.

d=\frac{192}{25}=7.68\text{ days.}

Example 6: inverse proportion worded problem y ∝ ⅟_x³

A cube of cheese has a density $d=1.075\text{g/cm}^{3}.$ The side length of the cube is $x=1.5cm.$ Another cube of cheese of the same mass has a density $d=1.072\text{g/cm}^{3}.$

What is the side length of the second cube of cheese? Write your answer to $3$ decimal places.

Write down the inverse proportion formula.

The density of an object is equal to its mass divided by its volume.

In the case of the cheese the density $d$ is inversely proportional to the cube of the side length $x$ . $d=\frac{k}{x^3}$ where $k$ is the constant of proportionality.

$k$ will represent the mass of the first cube of cheese.

Determine the value of $\textbf{k}$ .

As $d=1.075$ when $x=1.5,$ substituting these values into the formula, we get

$\begin{aligned} 1.075&=\frac{k}{1.5^{3}}\\\\ 1.075&=\frac{k}{3.375}\\\\ 1.075\times{3.375}&=k\\\\ k&=3.628125=\frac{1161}{320} \end{aligned}$

This is the mass of the cheese in grams.

Substitute $\textbf{k}$ and the known value into the inverse proportion formula.

Now we have the equation $d=\frac{3.628125}{x^{3}}.$ As the second cube has a density $d=1.072\text{g/cm}^{3},$ substituting this into the equation, we get

$1.072=\frac{3.628125}{x^{3}}$ .

Solve the equation.

\begin{aligned} 1.072\times{x}^{3}&=3.628125\\\\ x^{3}&=3.628125\div{1.072}\\\\ x^{3}&=3.384444963…\\\\ x&=\sqrt[3]{3.384444963…}\\\\ x&=1.50139795…\\\\ x&=1.501cm\text{ (3dp)} \end{aligned}

Common misconceptions

Modelling assumption

Whenever you solve word problems for inverse proportion you assume that everything has the same rate. For example, if the question involves the number of people working, we assume all the workers work at the same rate.

The constant of proportionality

For direct proportion, the constant of proportionality $k$ is the ratio of the two variables such as $k=y\div{x}.$ For inverse proportion, $k$ is the product of the two variables, such as $k=xy.$

The graph of an inversely proportional relationship does not cross either axis

The graph of any inversely proportional relationship cannot cross either axis. This is because, if we use the example $y\propto\frac{1}{x},$ if $x=0,$ the value for $y$ is undefined as we cannot divide a number by $0.$

If $y=0,$ then the value for the constant of proportionality must be $0$ or $x=0,$ but as we have just said, $x$ ≠ $0$ and so the relationship between $x$ and $y$ cannot exist for these two values as $k=0.$

Take care with writing time using the correct decimal

Time is used in some inverse proportion word problems. If an answer is $3.1$ you may be tempted to write it as $3$ hours $10$ minutes, but it would be $3$ hours $6$ minutes. (Remember there are $60$ minutes in an hour).

Graphs of the reciprocal function

The standard graph for $y\propto{x}$ is a straight line graph that passes through the origin with the gradient $k.$ The standard graph for $y\propto\frac{1}{x}$ is a curved line that does not cross either axis.

Related lessons on inverse proportion

Inverse proportion is part of our series of lessons to support revision on proportion. You may find it helpful to start with the main proportion lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Practice inverse proportion questions

160

40

20

10

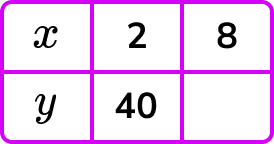
$y=\frac{k}{x}$ and so $k=xy.$

k=2\times{40}=80

y=\frac{80}{x}

When $x=8, \ y=\frac{80}{8}=10$ .

-29

6.7 \ (1d.p.)

15

13.3 \ (1d.p.)

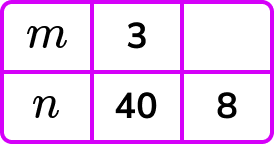
$n=\frac{k}{m^2}$ and so $k=m^{2} n.$

k=9\times{40}=360

n=\frac{360}{m^2}

When $n=8, \ m^2=\frac{360}{8}=45$

m=\sqrt{45} = 6.7 (1d.p.)

1.25

3.9 \ (1dp)

20

2

$b=\frac{k}{\sqrt{a}}$ and so $k=b\sqrt{a}.$

k=5\times{\sqrt{4}}=5\times{2}=10

b=\frac{10}{\sqrt{a}}

When $a=25, \ b=\frac{10}{\sqrt{25}}=\frac{10}{5}=2$ .

$20$ days

$24$ days

$12$ days

$108$ days

Let $p$ represent the number of people and $d$ represent the number of days of building, then

$d=\frac{k}{p}$ and so $k=dp.$

k=36\times{20}=720

d=\frac{720}{p}

When $p=60, \ d=\frac{720}{60}=12.$

$60$ minutes

$20$ minutes

$80$ minutes

$10$ minutes

Let $s$ represent speed and $t$ represent time taken, then

$s=\frac{k}{t}$ and so $k=st.$

k=8\times{40}=320

s=\frac{320}{t}

When $s=16,$

\begin{aligned} 16&=\frac{320}{t}\\\\ 16\times{t}&=320\\\\ t&=320\div{16}\\\\ t&=20 \end{aligned}

Note, the speed-distance-time formula is a known relationship (speed $=$ distance $\div$ time). For a constant distance, if the time taken to reach the destination increases, the speed must have decreased, or vice versa.

16

7

80

259

We have $c=\frac{k}{b^{2}}$ and so $k=b^{2}c.$

k=12^{2}\times{2.7}=388.8

c=\frac{388.8}{b^{2}}

When $c=1.5,$

\begin{aligned} 1.5&=\frac{388.8}{b^{2}}\\\\ 1.5\times{b^{2}}&=388.8\\\\ b^{2}&=388.8\div{1.5}\\\\ b^{2}&=259.2\\\\ b&=\sqrt{259.2}\\\\ b&=16.09968944…\\\\ b&=16\text{ bags} \end{aligned}

Inverse proportion GCSE questions

1. Let $y$ be inversely proportional to the square of $x.$

Complete the table.

Inverse proportion gcse question 1

(4 marks)

Show answer

k=x^{2}y=36 \times 2=72

(1)

$y=\frac{72}{x^{2}}$ or $y=72\div{2^{2}}$ or $y=72\div{12^{2}}$

(1)

18

(1)

0.5

(1)

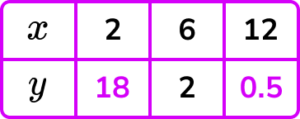
Inverse proportion gcse question 1 answer

2. It takes $6$ workers $24$ hours to build an emergency flood barrier.

The wall needs to be built in $8$ hours.

How many workers are needed to build the same emergency flood barrier in $8$ hours?

(2 marks)

Show answer

6\times 3

(1)

$18$ workers

(1)

3. It takes $360$ minutes to fill a swimming pool from $5$ taps.

(a) How many minutes would it take $3$ taps to fill the swimming pool?

(b) State one assumption you made in working out your answer to part (a).

(3 marks)

Show answer

(a)

k=xy=360 \times 5=1800

(1)

$1800 \div 3=600$ minutes

(1)

(b)

All taps work at the same rate.

(1)

Learning checklist

You have now learned how to:

Solve problems involving inverse proportion, including algebraic representations

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.