Direct proportion formula

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Substitution Rearranging formulae

This topic is relevant for:

GCSE Maths Ratio and Proportion Proportion Direct Proportion

Direct Proportion Formula

Here we will learn about direct proportion formulas, including what the proportion formulas are and how to interpret them.

There are also direct proportion formula worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the direct proportion formula?

The direct proportion formula is an algebraic formula which represents the directly proportional relationship between two variables.

Direct proportion is one type of a proportionality relationship. As one value increases, so does the other value.

The proportionality symbol is ∝. If the variables $x$ and $y$ are directly proportional then we can write the relationship using the proportionality symbol.

y\propto x

We can also write this as a formula using the constant of proportionality, $k.$

$k$ is a constant value that links the two variables.

y=kx

Proportional relationships can also be represented by graphs.

The following is a type of direct proportion graph.

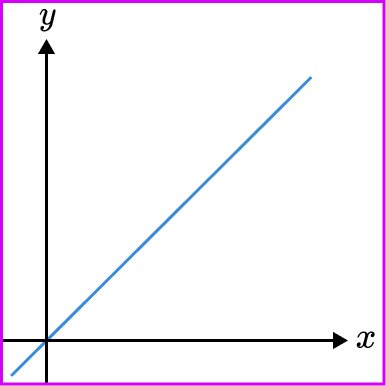
It is a straight line graph going through the origin. It has the equation $y=kx$ .

Direct proportion formulas can involve powers and roots. If the variables were $x$ and $y,$ and $y$ is directly proportional to $x^{2},$ we can write the relationship using the proportionality symbol.

y\propto x^2

We can also write this as a formula using the constant of proportionality $k.$

y=kx^2

The graph of this relationship would be quadratic and have the shape of a parabola.

What is the direct proportion formula?

How to recognise a direct proportion formula

In order to recognise a direct proportion formula:

Look for an equation in the form $y=kx^n.$
Check there are no other terms in the equation.

Explain how to recognise a direct proportion formula

Direct proportion worksheet (includes direct proportion formula)

Get your free direct proportion formula worksheet of 20+ direct proportion questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Direct proportion worksheet (includes direct proportion formula)

Get your free direct proportion formula worksheet of 20+ direct proportion questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Direct proportion formula examples

Example 1: recognise the direct proportion formula

Which of these equations indicate that $y\propto x?$

A B C D

y=x+5 \hspace{1cm} y=\frac{5}{x} \hspace{1cm} y=1-5x \hspace{1cm} y=5x

Look for an equation in the form $y=kx^n.$

We are looking for a direct proportion equation. We are looking for an equation with the variable, $x^n,$ being multiplied by a number.

We can eliminate equation B as this has a $\frac{1}{x}$ term, this would be inverse proportion.

2Check there are no other terms in the equation.

For direct proportion there can be no addition or subtraction involved in the equation.

So we can eliminate equations A and C.

The only equation which only has an $x^n$ -term being multiplied by a number is equation D. Here the power of the $x$ is $1$ .

$y=5x$ indicates that $y \propto x.$

Example 2: recognise the direct proportion formula

Which of these equations indicate that a direct proportion?

A B C D

y=\frac{4}{x} \hspace{1cm} y=4x^2 \hspace{1cm} y=4x-3 \hspace{1cm} y=4x+2

Look for an equation in the form $y=kx^n.$

We are looking for a direct proportion equation. We are looking for an equation with the variable, $x^n,$ being multiplied by a number.

We can eliminate equation A as this has a $\frac{4}{x}$ term, this would be inverse proportion.

Check there are no other terms in the equation.

For direct proportion there can be no addition or subtraction involved in the equation.

So we can eliminate equations C and D.

The only equation that only has an $x^n$ -term being multiplied by a number is equation B. Here the power of the $x$ is $2$ .

$y=4x^2$ indicates $y\propto x^2.$

How to construct a direct proportion formula

In order to construct a direct proportion formula:

Write down the general proportion formula.
Find the constant $\textbf{k}$ , the constant of proportionality.
Write down the equation.

Explain how to construct a direct proportion formula

Constructing direct proportion formula examples

Example 3: constructing a direct proportion equation

$y$ is directly proportional to $x.$

When $y=35, \ x=5.$

Find a formula for $y$ in terms of $x.$

Write down the general proportion formula.

From the first sentence we can write down the relationship as

$y\propto x.$

We can then write this as a formula using the constant of proportionality $k,$

$y=kx$ .

Where $k$ is the constant of proportionality.

Find the constant of proportionality.

We can find the constant of proportionality by substituting in the corresponding values we are given.

We are told ‘when $y=35, \ x=5’.$

$\begin{aligned} y&= kx \\\\ 35 &= k \times 5 \\\\ k&=35 \div 5=7 \end{aligned}$

Write down the equation.

To finish off we can write the direct proportion equation as

$y=7x.$

Example 4: constructing a direct proportion equation

$y$ is directly proportional to $x.$

When $y=4, \ x=20.$

Find a formula for $y$ in terms of $x.$

Write down the general proportion formula.

From the first sentence we can write down the relationship as

$y\propto x.$

We can then write this as a formula using the constant of proportionality $k,$

$y=kx$ .

Where $k$ is the constant of proportionality.

Find the constant of proportionality.

We can find the constant of proportionality by substituting in the corresponding values we are given.

We are told ‘when $y=4, \ x=20’.$

$\begin{aligned} y&= kx \\\\ 4 &= k \times 20 \\\\ k&=4 \div 20=0.2 \end{aligned}$

Write down the equation.

To finish off we can write the direct proportion equation as

$y=0.2x \ \text{or} \ y=\frac{x}{5}.$

Example 5: constructing a direct proportion equation involving a power or root

$y$ is directly proportional to $\sqrt{x}.$

When $y=40, \ x=4.$

Find a formula for $y$ in terms of $x.$

Write down the general proportion formula.

From the first sentence we can write down the relationship as

$y\propto \sqrt{x}.$

We can then write this as a formula using the constant of proportionality $k,$

$y=k\sqrt{x}$ .

Where $k$ is the constant of proportionality.

Find the constant of proportionality.

We can find this unknown value, the constant of proportionality by substituting in the corresponding values we are given.

We are told ‘when $y=40, \ x=4’.$

$\begin{aligned} y&= k\sqrt{x} \\\\ 40 &= k\times \sqrt{4} \\\\ 40 &= k\times 2 \\\\ k&=40 \div 2=20 \end{aligned}$

Write down the equation.

To finish off we can write the direct proportion equation as

$y=20\sqrt{x}.$

Common misconceptions

Confusing direct proportion and inverse proportion

You will need to learn which formula is for which type of proportionality.

Direct proportion	Inverse proportion
$y\propto x^n$	$y\propto \frac{1}{x^n}$
$y=kx^n$	$y=\frac{k}{x^n}$

Not recognising and applying any powers or roots

Most direct proportional formulas just involve $x,$ but they can involve powers such as $x^{2}$ or roots such as $\sqrt{x}$ . $\sqrt{x}$ is the same as $x^{\frac{1}{2}}$ .

Assuming the constant of proportionality can only be an integer

The constant of proportionality can be an integer (a whole number), but they can also be decimals or fractions.

For example,

$y=\frac{x}{2}$

Even though there is a fraction, the constant of proportionality is $\frac{1}{2}$ or $0.5.$

$y=\frac{x}{2}=\frac{1}{2} \times x=0.5 \times x$

Related lessons on direct proportion formula

Direct proportion formula is part of our series of lessons to support revision on proportion. You may find it helpful to start with the main proportion lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Practice direct proportion formula questions

y=2x

y=x+2

y=\frac{x}{2}

y=20x

For direct proportion there can be no addition or subtraction involved in the equation. The incorrect equation is $y=x+2.$

y=x+5

y=5x

y=\frac{5}{x}

y=5x^2

For direct proportion there can be no addition or subtraction involved in the equation. The correct equation is $y=5x.$

y=4-10x

y=10x+4

y=\frac{10}{x^2}

y=10x^3

For direct proportion there can be no addition or subtraction involved in the equation. The correct equation is $y=10x^3.$

y=4x

y=\frac{3}{x}

y=\frac{x}{4}

y=3x

Write down the relationship between $y$ and $x$ and substitute the given values to find $k,$ the constant of proportionality.

\begin{aligned} y&\propto x \\\\ y&= kx \\\\ 24 &= k\times 8 \\\\ k&=24\div 8=3 \end{aligned}

So, the equation is

y=3x.

y=50x

y=2x

y=\frac{x}{2}

y=\frac{2}{x}

Write down the relationship between $y$ and $x$ and substitute the given values to find $k,$ the constant of proportionality.

\begin{aligned} y&\propto x \\\\ y&= kx \\\\ 10&= k\times 5 \\\\ k&=10\div 5=2 \end{aligned}

So, the equation is

y=2x.

y=6x

y=2x^2

y=6x^2

y=3x

Write down the relationship between $y$ and $x$ and substitute the given values to find $k,$ the constant of proportionality.

\begin{aligned} y&\propto x^2 \\\\ y&= kx^2 \\\\ 18&= k\times 3^2 \\\\ 18&= 9k \\\\ k&=18\div 3=2 \end{aligned}

So, the equation is

y=2x^2.

Direct proportion formula GCSE questions

1. $y$ is directly proportional to $x$ and $k$ is a constant.

Identify the correct equation.

Equation A – $y=\frac{k}{x}$

Equation B – $y=kx$

Equation C – $y=k-x$

Equation D – $y=\frac{x}{k}$

(1 mark)

Show answer

Equation B

(1)

2. $y$ is proportional to $x.$

When $y=36, \ x=12.$

(a) Find the equation for $y$ in terms of $x.$

(b) Find the value of $x$ when $y=50.$

(4 marks)

Show answer

(a)

\begin{aligned} y&=kx \\\\ 36&=k \times 12 \\\\ k&=36 \div 12=3 \end{aligned}

(1)

y=3x

(1)

(b)

$50=3x \$ so $\ x=50 \div 3$

(1)

x=\frac{50}{3}=16\frac{2}{3}

(1)

3. $m$ is directly proportional to $p$ .

When $p=5, \ m=20.$

Find $m$ when $p=3.$

(3 marks)

Show answer

$m=kp \$ or $\ 20=k \times 5$

(1)

$k=4 \$ or $\ m=4p$

(1)

m=12

(1)

Learning checklist

You have now learned how to:

Recognise a direct proportion formula

Construct a direct proportion equation

Model situations by translating them into algebraic formulae

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.