GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Arithmetic Multiplying decimals Dividing decimals Proportion Lowest common multiple Highest common factor Enlargement Scale factor Converting metric units Fractions of amounts Percentage of an amount Laws of indicesThis topic is relevant for:
Best Buy Maths
Here we will learn about best buy maths, including the unitary method, common multiples (including LCM), exchange rates and shopping deals.
There are also best buy maths worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is best buy maths?
Best buys problems involve assessing which item is the best value for money.
To do this we could use the following methods,
Unitary method – this involves calculating the price per unit for each item.
Common multiples – here we find a common multiple of the number of units we have and use this make comparisons.
Shop deals – we interpret deals such as ‘ 3 for 2 ’, ‘buy one get one free’ or a percentage extra free.
Exchange rates – if the prices are in different currencies, we convert them to the same currency to compare them.
In a question you may be asked which of 2 or more products is the better value. This would indicate that you are being asked to find which of the products is the best buy.
Best buy problems may also be known as cost problems. We have to compare the cost of 2 or more items and then decide which of the items is the best value.
What is best buy?
How to use best buy maths
In order to compare deals:
- Note the cost of the items and the number of items for each deal.
- Calculate the price for an equivalent number of items for each deal.
For the unitary method, this is the price of a single item. For the common multiples method, this is the price of a common number of items. - Compare the prices of the equivalent quantities.
In order to use exchange rates:
- Identify the exchange rate and currency to be converted.
- Convert the currency.
- Compare the values in the same currency to identify the best value.
Explain how to use best buy maths
Best buy maths worksheet
Get your free best buy maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE Best buy maths worksheet
Get your free best buy maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEBest buy maths examples
Example 1: unitary method
| Offer A | Offer B |
|---|---|
| 3 footballs | 7 footballs |
| £12 | £35 |
- Note the cost of the items and the number of items for each deal.
In this example, we are told that 3 footballs = £12 and 7 footballs = £35.
2Calculate the price for an equivalent number of items for each deal.
For the unitary method, this is the price of a single item. For the common multiples method, this is the price of a common number of items.
In this example we are going to use the unitary method, calculating the price of 1 football for each deal.
3Compare the prices of the equivalent quantities.
Offer A is better value as £4 per football is cheaper than £5 per football.
Step-by-step guide: Unitary method (coming soon)
Example 2: unitary method
| Offer A | Offer A |
|---|---|
| 2kg of pasta | 1.5kg of pasta |
| £4.40 | £3.60 |
Note the cost of the items and the number of items for each deal.
In this example we are told that 2kg of pasta = £4.40 and 1.5kg of pasta = £3.60.
Calculate the price for an equivalent number of items for each deal.
For the unitary method, this is the price of a single item. For the common multiples method, this is the price of a common number of items.
We are going to use the unitary method and calculate the price of 1kg of pasta for each deal.
Compare the prices of the equivalent quantities.
Offer A is better value as £2.20 per kilogram of pasta is cheaper than £2.40 per kilogram of pasta.
Alternatively we could work out how much pasta can be bought for £1.
Here we can see that Offer A gives us more pasta per £, so is better value.
Example 3: common multiples
| Offer A | Offer A |
|---|---|
| 3 t-shirts | 4 t-shirts |
| £14 | £18 |
Note the cost of the items and the number of items for each deal.
In this example we are told that 3 t-shirts =£14 and 4 t-shirts =£18.
Calculate the price for an equivalent number of items for each deal.
For the unitary method, this is the price of a single item. For the common multiples method, this is the price of a common number of items.
This time we are going to use common multiples. This method is useful when the total prices are not easily divisible by the number of items.
12 is a common multiple of 3 and 4 so we are going to find the price of 12 t-shirts using each offer.
Compare the prices of the equivalent quantities.
Offer B is better value since the same number of t-shirts would cost less using this offer.
Example 4: common multiples
| Offer A | Offer B | Offer C |
|---|---|---|
| 200ml cola | 500ml cola | 1l cola |
| £0.80 | £1.80 | £3.50 |
Note the cost of the items and the number of items for each deal.
Here we are told that 200ml=£0.80, \ 500ml=£1.80 and 1l, or 1000ml=£3.50.
Calculate the price for an equivalent number of items for each deal.
For the unitary method, this is the price of a single item. For the common multiples method, this is the price of a common number of items.
The easiest method to use here is the common multiples method.
1000 is a common multiple of 200, 500 and 1000 so we are going to find the price of 1000ml for each offer.
Compare the prices of the equivalent quantities.
Offer C is the best value since £3.50 is the lowest cost for 1000ml of cola.
Example 5: deals
A shop is selling the same jumper on two different offers.
Which offer is better value for money?
| Offer A | Offer B |
|---|---|
| Buy one get one free | 3 for 2 |
| Jumpers cost £20 | Jumpers cost £18 each |
Note the cost of the items and the number of items for each deal.
For this question we need to think more carefully.
For Offer A, which is buy one get one free, we will get 2 jumpers for £20.
For Offer B, which is 3 for 2, we will get 3 jumpers for £18 \times 2=£36.
Calculate the price for an equivalent number of items for each deal.
For the unitary method, this is the price of a single item. For the common multiples method, this is the price of a common number of items.
Applying the unitary method we can calculate the price of one jumper for each offer.
Compare the prices of the equivalent quantities.
Offer A is better since the cost of each jumper is less.
Example 6: deals
A shop is selling the same chocolate bars on two different offers.
Which offer is better value for money?
| Offer A | Offer B |
|---|---|
| 20\% off the price | 50\% extra free |
| 250g bar costs £5 | 120g bar costs £3 |
Calculate the total cost of the items and the total number of items for each deal.
For Offer A, we need to reduce the price by 20\%.
20\% of £5= £1
£5-£1=£4
The price of a 250g bar is £4.
For Offer B, we need to increase the weight of the bar by 50\%.
50\% of 120g=60g
120g+60g=180g
The price for a 180g bar is £3.
Calculate the price for an equivalent number of items for each deal.
For the unitary method, this is the price of a single item. For the common multiples method, this is the price of a common number of items.
We are going to calculate the price of 1g of chocolate for each deal.
Compare the prices of the equivalent quantities.
Offer A is better since 1g of chocolate costs less using Offer A.
Example 7: exchange rates
The exchange rate is £1 = \$1.50.
A pair of trainers cost £60 in the UK.
The same pair of trainers cost \$100 in the USA.
Where is it cheaper to buy the trainers?
Identify the exchange rate and currency to be converted.
The exchange rate is £1 = \$1.50.
We need to convert £60 to \$ so that the currencies are the same and we can compare the amounts.
Convert the currency.
Converting £60 to \$: £60 \times 1.50 = \$90
Compare the values in the same currency to identify the best value.
The trainers cost \$90 in the UK.
The trainers cost \$100 in the USA.
They are cheaper in the UK.
Step-by-step guide: Exchange rates (coming soon)
Example 8: exchange rates
The exchange rates are £1 = \$1.40 and £1 = €1.30.
A game costs £30 in the UK.
The same game costs \$49 in the USA and €32.50 in France.
Where is it cheapest to buy the game?
Identify the exchange rate and currency to be converted.
The exchange rates are £1 = \$1.40 and £1 = €1.30.
Since both of the exchange rates involve £, we are going to convert all of the prices to £.
Convert the currency.
Convert \$49 and €32.50 to £ .
\$49 \div 1.40 = £35
€32.50 \div 1.30 = £25
Compare the values in the same currency to identify the best value.
The game costs £30 in the UK, £35 in the USA and £25 in France.
It is the cheapest in France.
Common misconceptions
- Understanding your calculation
For example, if 10 tennis balls cost £5, the price per ball would be £5 \div 10=£0.50.
An alternative would be to calculate 10 \div 5=2 which is actually the number of balls for £1. Each method is correct as long as it is comparable to the other offer and you compare them correctly.
- Incorrect use of the exchange rate when converting currencies
If £1= \$1.30, to convert £ to \$ we need to multiply by 1.30. To convert \$ to £ we need to divide by 1.30.
- Adding and subtracting amounts rather than using a multiplier
As you need to maintain proportion of amounts you should only multiply or divide to compare equivalence of amounts or values. Adding and subtracting does not maintain proportion.
Practice best buy maths questions
1. Which offer is better value for money?
| Offer A | Offer B |
| 5 melons | 8 melons |
| £15 | £16 |
Offer A: each melon is £3.
Offer B: each melon is £2.
Offer B is better value for money.
Offer A: each melon is £3.
Offer B: each melon is £2.
Offer A is better value for money.
Offer A: each melon is £15.
Offer B: each melon is £16.
Offer A is better value for money.
Offer A: each melon is £2.
Offer B: each melon is £3.
Offer A is better value for money.
Offer A, 15 \div 5 = £3 per melon.
Offer B, 16 \div 8 = £2 per melon.
So Offer B is better value for money.
2. Which offer is better value for money?
| Offer A | Offer B |
| 250 ml of shampoo | 400ml of shampoo |
| £1.25 | £1.60 |
Offer A: 1 \ ml is 5p.
Offer B: 1 \ ml is 4p.
Offer A is better value for money.
Offer A: 1 \ ml is 0.5p
Offer B: 1 \ ml is 0.4p.
Offer B is better value for money.
Offer A: 1 \ ml is £5.
Offer B: 1 \ ml is £4.
Offer B is better value for money.
Offer A: 1 \ ml is £0.50.
Offer B: 1 \ ml is £0.40
Offer B is better value for money.
Write the prices in pence.
Offer A, 125 \div 250 = 0.5 so 0.5 pence per ml.
Offer B, 160 \div 400 = 0.4 so 0.4 pence per ml.
So Offer B is better value for money.
3. Which offer is the best value for money?
| Offer A | Offer B | Offer C |
| 3 pizzas | 5 pizzas | 15 pizzas |
| £24 | £35 | £135 |
Offer A: 1 pizza for £9.
Offer B: 1 pizza for £7.
Offer C: 1 pizza for £8.
So Offer B is the best value for money.
Offer A: 1 pizza for £7.
Offer B: 1 pizza for £8.
Offer C: 1 pizza for £9.
So Offer A is the best value for money.
Offer A: 1 pizza for £8.
Offer B: 1 pizza for £7.
Offer C: 1 pizza for £9.
So Offer C is the best value for money.
Offer A: 1 pizza for £8.
Offer B: 1 pizza for £7.
Offer C: 1 pizza for £9.
So Offer B is the best value for money.
Offer A, 24 \div 3 = 8 so £8 per pizza.
Offer B, 35 \div 5 = 7 so £7 per pizza.
Offer C, 135 \div 15 = 9 so £9 per pizza.
So Offer B is the best value for money.
4. A shop is selling the same pens on two different offers.
Which offer is better value for money?
| Offer A | Offer B |
| Buy one get one free | 3 for 2 |
| Pens cost £3.20 each | Pens cost £2.25 each |
Offer A is £3.20 per pen and Offer B is £2.25 per pen so Offer B is better value for money.
Offer A is £1.60 per pen and Offer B is £1.50 per pen so Offer B is better value for money.
Offer A is £6.40 per pen and Offer B is £4.50 per pen so Offer B is better value for money.
Offer A is £6.40 per pen and Offer B is £6.75 per pen so Offer A is better value for money.
Offer A is a total of £3.20 for two pens which means that each pen costs £1.60.
Offer B is a total of £4.50 for three pens which means that each pen is £1.50.
Therefore Offer B is better value for money.
5. A shop is selling the same chocolate bar on two different offers.
Which offer is better value for money?
| Offer A | Offer B |
| 10% off the price | 25% extra free |
| 360g bar costs £2 | 200g bar costs £1.60 each |
Offer A is 50p per 100g and Offer B is 64p per 100g so Offer A is better value for money.
Offer A is £1.80 per 250g and Offer B is £1.60 per 250g so Offer B is better value for money.
Offer A is £2 per 100g and Offer B is £1.56 per 100g so Offer B is better value for money.
Offer A is 180g per £1 and Offer B is 125g per £1 so Offer B is better value for money.
Offer A: 10\% of £2 = £0.20
£2-£0.20=£1.80 so 360g for £1.80.
£1.80 \div 3.6 =£0.50 so 50p per 100g.
Offer B: 25\% of 200g = 50g
200g + 50g = 250g so 250g for £1.60.
£1.60 \div 2.5 =£0.64 so 64p per 100g.
6. The exchange rate is £1 = \$1.20.
A jumper costs £40 in the UK.
The same jumper costs \$45 in the USA.
Where is it cheaper to buy the jumper?
UK: £40
USA: 45 \times 1.20 = £54
The jumper is cheaper in the UK.
UK: 40 \times 1.20=\$48
USA: \$45
The jumper is cheaper in the USA.
UK: 40 \div 1.20=\$33.33
USA: \$45
The jumper is cheaper in the UK.
UK: 40 \times 1.20=\$48
USA: 45 \div 1.20=£37.50
The jumper is cheaper in the USA.
The exchange rate is £1 = \$1.20 so you need to multiply the price in pounds by 1.20.
UK: 40 \times 1.20=\$48
Best buy maths GCSE questions
1. Packs of pens are sold in two sizes.
12 pens cost £3
20 pens cost £4
Which size pack is better value for money?
You must show your working.
(3 marks)
12 pack, 1 pen is 25p .
(1)
20 pack, 1 pen is 20p .
(1)
20 pack is better value for money.
(1)
2. (a) A shop is selling pictures.
A 10cm by 15cm picture costs £45.
An enlargement of the same picture is for sale.
The enlargement measures 12cm by 18cm and costs £86.40.
Which picture is better value for money?
(b) Why might you choose the picture that is not the best value for money?
(5 marks)
(a)
Calculate area of a picture,
10 \times 15=150cm^2or
12 \times 18=216cm^2 .
(1)
Calculates price of equivalent unit, for example price per square centimetre,
£45 \div 150=£0.30 per square centimetre
or
£86.40 \div 216 =£0.40 per square centimetre.
(1)
Calculates both equivalent values correctly.
£0.30 per square centimetre
and
£0.40 per square centimetre.
(1)
The smaller picture is better value for money as it costs 30p per square centimetre.
(1)
(b)
You might want a larger picture.
(1)
3. Michael wants to exchange some money from pounds to Euros. Two shops are offering different exchange rates. These are represented in the graph below.
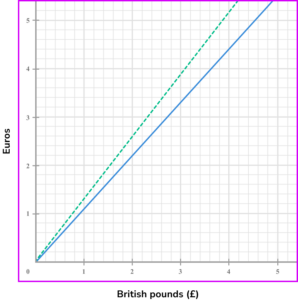
The green dotted line represents Your Money and the blue solid line represents Cash for Travellers.
(a) Which shop has a better exchange rate and how do you know from looking at the graph?
(b) What are the exchange rates that each shop is offering?
(4 marks)
(a)
Identifies that Your Money has the better exchange rate.
(1)
Identifies that Your Money has a steeper gradient.
(1)
(b)
Your Money, £1 = €1.30 .
Cash for travellers, £1 = €1.10 .
Calculates the gradient of one line.
(1)
Calculates the gradient of the second line.
(1)
Learning checklist
You have now learned how to:
- Calculate value for money using a unitary method
- Calculate value for money using common multiples and common factors
- Calculate value for money with deals such as buy one get one free and 3 for the price of 2
- Use exchange rates to convert money to different currencies
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.
Find out more about our GCSE maths tuition programme.