Reciprocal maths

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Decimals Fractions Improper fractions and mixed numbers Simplifying fractions

This topic is relevant for:

GCSE Maths Number Types Of Numbers

Reciprocal Maths

Here we will learn about reciprocals, including the definition of reciprocal and how to find reciprocals.

There are also reciprocal worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a reciprocal?

The reciprocal of a number is $1$ divided by the number. It can also be found by raising the number to the power of $-1$ .

The reciprocal, also called the multiplicative inverse, is found by writing the original number as a fraction and “flipping” it.

When we multiply a number by its reciprocal, the answer is always $1.$

For example,

Every number has a reciprocal except $0 \ (1 \div 0$ is undefined).

Given that the method of finding a reciprocal is to flip the number when it is written as a fraction, you might notice that the reciprocal of a reciprocal is the original number.

For example, the reciprocal of $5$ is $\frac{1}{5}$ and the reciprocal of $\frac{1}{5}$ is $\frac{5}{1}=5.$

What is a reciprocal?

Reciprocal graphs

Reciprocal functions produce distinctive looking graphs. Here is the graph of $y=\frac{1}{x},$ the basic reciprocal function.

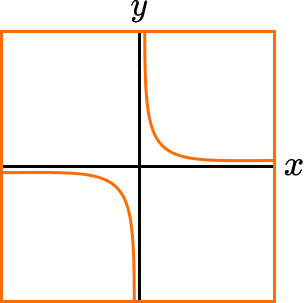
Notice that the graph is undefined for $x=0$ since we cannot calculate $1 \div 0.$

Step-by-step guide: Reciprocal graphs

How to write the reciprocal of a number

In order to write the reciprocal of a number:

Without a calculator:

Write the number as a fraction.
“Flip” the fraction.

Alternatively, if you have a calculator:

Divide $\bf{1}$ by the number or raise the number to the power of $\bf{-1}$ .

Explain how to write the reciprocal of a number

Reciprocal maths worksheet

Get your free reciprocal maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Reciprocal maths worksheet

Get your free reciprocal maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Reciprocal maths examples

Example 1: reciprocal of a whole number

Write down the reciprocal of $7.$

Write the number as a fraction.

First we write the number $7$ as a fraction. $7$ is the numerator and $1$ is the denominator.

7=\frac{7}{1}.

2“Flip” the fraction.

Then we can “flip” the fraction by inverting it, or turning it upside down.

So the reciprocal of the number $7$ is

\frac{1}{7}.

Example 2: reciprocal of a fraction

Write down the reciprocal of $\frac{2}{3}.$

Write the number as a fraction.

The number is already a fraction,

$\frac{2}{3}.$

“Flip” the fraction.

Then we can “flip” the fraction by inverting it, or turning it upside down.

So the reciprocal of $\frac{2}{3}$ is

$\frac{3}{2}.$

This can also be written as $1 \frac{1}{2}$ or $1.5.$

Example 3: reciprocal of an improper fraction

Write down the reciprocal of $\frac{9}{5}.$

Write the number as a fraction.

The number is already a fraction,

$\frac{9}{5}.$

“Flip” the fraction.

Then we can “flip” the fraction by inverting it, or turning it upside down.

So the reciprocal of $\frac{9}{5}$ is

$\frac{5}{9}.$

Example 4: reciprocal of a mixed number

Write down the reciprocal of $3\frac{1}{2}.$

Write the number as a fraction.

To find the reciprocal of a mixed fraction, it needs to be changed to an improper fraction.

$3\frac{1}{2}=\frac{7}{2}.$

“Flip” the fraction.

Then we can “flip” the fraction by inverting it, or turning it upside down.

So the reciprocal of $3\frac{1}{2}$ is

$\frac{2}{7}.$

Example 5: reciprocal of a decimal number less than 1

Write down the reciprocal of $0.3.$

Write the number as a fraction.

The number needs to be changed to a fraction,

$0.3=\frac{3}{10}.$

“Flip” the fraction.

Then we can “flip” the fraction by inverting it, or turning it upside down.

So the reciprocal of $0.3$ is

$\frac{10}{3}.$

This can also be written as $3 \frac{1}{3}.$

Example 6: reciprocal of a decimal number greater than 1

Write down the reciprocal of $4.8.$

Write the number as a fraction.

The number needs to be changed to a fraction,

$4.8=4\frac{8}{10}=\frac{48}{10}.$

“Flip” the fraction.

Then we can “flip” the fraction by inverting it, or turning it upside down.

So the reciprocal of $4.8$ is

$\frac{10}{48}.$

This can be simplified to $\frac{5}{24}.$

Example 7: reciprocal of a negative number

Write down the reciprocal of $-3.$

Write the number as a fraction.

The number needs to be changed to a fraction.

$-3=\frac{-3}{1}.$

“Flip” the fraction.

Then we can “flip” the fraction by inverting it, or turning it upside down.

So the reciprocal of $-3$ is

$\frac{1}{-3}=-\frac{1}{3}.$

Here $1 \div (-3)=-\frac{1}{3}$ therefore we can move the negative sign in front of the fraction.

Common misconceptions

Reciprocal of zero

Zero does not have a reciprocal. This is because $1 \div 0$ is undefined (it does not exist).

Fractions and decimals

Whilst some fractions can easily be written as decimals, many fractions cannot be written as exact decimals. When this is the case, leave your answer as a fraction as it is more accurate.

For example, $\frac{3}{4}=0.75$ so you could use either for your answer.

$\frac{1}{7}$ cannot be written as an exact decimal so leave your answer as a fraction.

Practice reciprocal maths questions

1.9

-\frac{1}{9}

\frac{1}{9}

0.9

To find the reciprocal of $9$ we first write it as a fraction with 1 as the denominator. Then we turn the fraction upside down.

$9=\frac{9}{1}$

So the reciprocal is $\frac{1}{9}.$

6.11

\frac{11}{6}

-\frac{11}{6}

11.6

To find the reciprocal we turn the fraction upside down.

So the reciprocal is $\frac{11}{6}.$

0.625

62.5

\frac{8}{13}

\frac{5}{13}

To find the reciprocal we turn the fraction upside down.

So the reciprocal is $\frac{5}{8}.$

As a decimal this is $0.625.$

4.15

\frac{41}{5}

\frac{5}{21}

41.5

We first need to write this mixed number as an improper fraction. Then we can turn the fraction upside down.

$4\frac{1}{5}=\frac{21}{5}$

So the reciprocal is $\frac{5}{21}.$

1.2

1.25

1.3

8

To find the reciprocal of $0.8$ we first write it as a fraction. Then we turn the fraction upside down.

$0.8=\frac{8}{10}$

So the reciprocal is $\frac{10}{8}.$

This can be written as $1.25.$

6.5

\frac{28}{5}

-5.6

\frac{5}{28}

To find the reciprocal of $5.6$ we first write it as an improper fraction. Then we turn the fraction upside down.

$5.6=5\frac{6}{10}=\frac{56}{10}$

So the reciprocal is $\frac{10}{56}.$

This can be simplified to $\frac{5}{28}.$

Reciprocal maths GCSE questions

1. Write down the reciprocal of $\frac{1}{8}$ .

(1 mark)

Show answer

8

(1)

2. Find the reciprocal of $\frac{3}{11}$ . Write your answer as a mixed number.

(2 marks)

Show answer

\frac{11}{3}

(1)

3\frac{2}{3}

(1)

3. Find the reciprocal of $3.1.$

(2 marks)

Show answer

3.1=\frac{31}{10}

(1)

\frac{10}{31}

(1)

Learning checklist

You have now learned how to:

Find the reciprocal of an integer

Find the reciprocal of a fraction or a decimal number

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.