Laws of indices

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Negative numbers Arithmetic Fractions to decimals

This topic is relevant for:

GCSE Maths Algebra

Laws Of Indices

Laws of Indices

Here we will learn everything you need to know about the laws of indices for GCSE & iGCSE maths (Edexcel, AQA and OCR). You’ll learn what the laws of indices are and how we can use them. You’ll learn how to multiply indices, divide indices, use brackets and indices, how to raise values to the power of 0 and to the power of 1, as well as fractional and negative indices.

Look out for the index laws worksheet and exam questions at the end.

What are the laws of indices?

Laws of indices provide us with rules for simplifying calculations or expressions involving powers of the same base. This means that the larger number or letter must be the same.

For example,

\[2^{5} \times 2^{3}=2^{8}\]

\[x^{10} \div x^{4}=x^{6}\]

We cannot use laws of indices to evaluate calculations when the bases are different

For example,

\[2^{5} \times 3^{3}\]

\[x^{10} \div y^{4}\]

We can however evaluate these calculations. Check out our other pages to find out how.

What are the laws of indices?

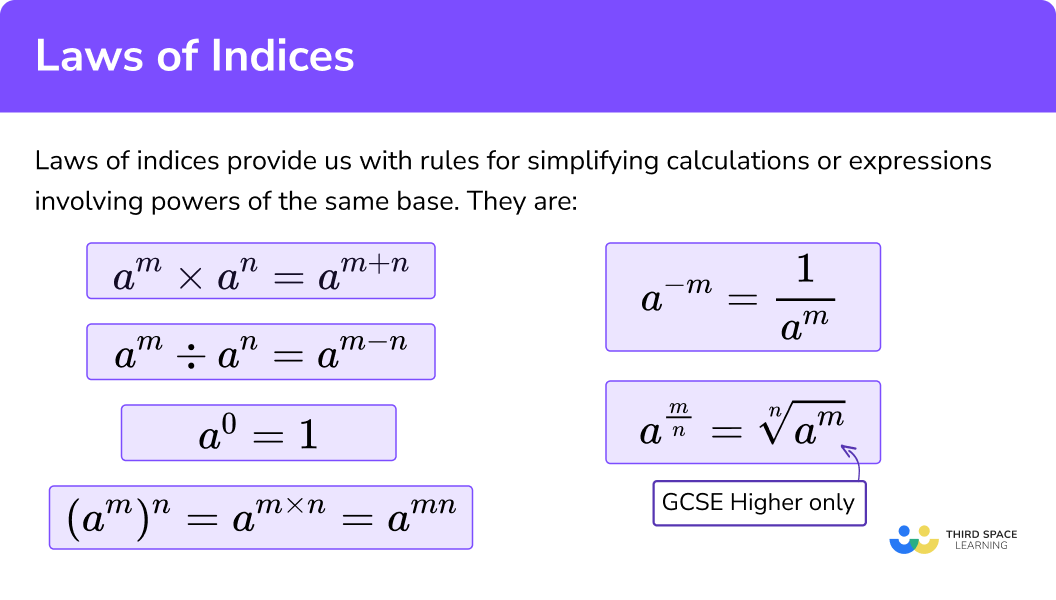
What are the 6 laws of indices?

The 6 laws of indices are:

Multiplying indices
Dividing indicies
Brackets with indices
Power of 0
Negative indices
Fractional indices

For examples and practice questions on each of the rules of indices, as well as how to evaluate calculations with indices with different bases, follow the links below.

See also: Index notation

Index laws worksheet

Get your free laws of indices worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Index laws worksheet

Get your free laws of indices worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Laws of indices methods

Law 1: Multiplying indices

When multiplying indices with the same base, add the powers.

\[a^{m} \times a^{n}=a^{m+n}\]

Step-by-step guide: Multiplying indices

Law 2: Dividing indices

When dividing indices with the same base, subtract the powers.

\[a^{m} \div a^{n}=a^{m-n}\]

Step-by-step guide: Dividing indices

Law 3: Brackets with indices

When there is a power outside the bracket multiply the powers.

\[(a^{m})^{n}=a^{m \times n}\]

Step-by-step guide: Brackets with indices

Law 4: Power of 0

Any non-zero value raised to the power of 0 is equal to 1.

\[a^{0}=1\]

Step-by-step guide: Power of 0

Law 5: Negative indices

When the index is negative, put it over 1 and flip (write its reciprocal) to make it positive.

\[a^{-m}=\frac{1}{a^{m}}\]

Step-by-step guide: Negative indices

Law 6: Fractional indices

When the index is a fraction, the denominator is the root of the number or letter, then raise the answer to the power of the numerator.

\[x^{\frac{a}{b}}=(\sqrt[b]{x})^{a}\]

Step-by-step guide: Fractional indices

What are indices?

An index is a small number that tells us how many times a term has been multiplied by itself.

The plural of index is indices.

Below is an example of a term written in index form:

\[4^{3}\]

4 is the base and 3 is the index.

We can read this as ‘4 to the power 3’

Another way of expressing 4³ is

\[4 \times 4 \times 4=64\]

Indices can be positive or negative numbers.

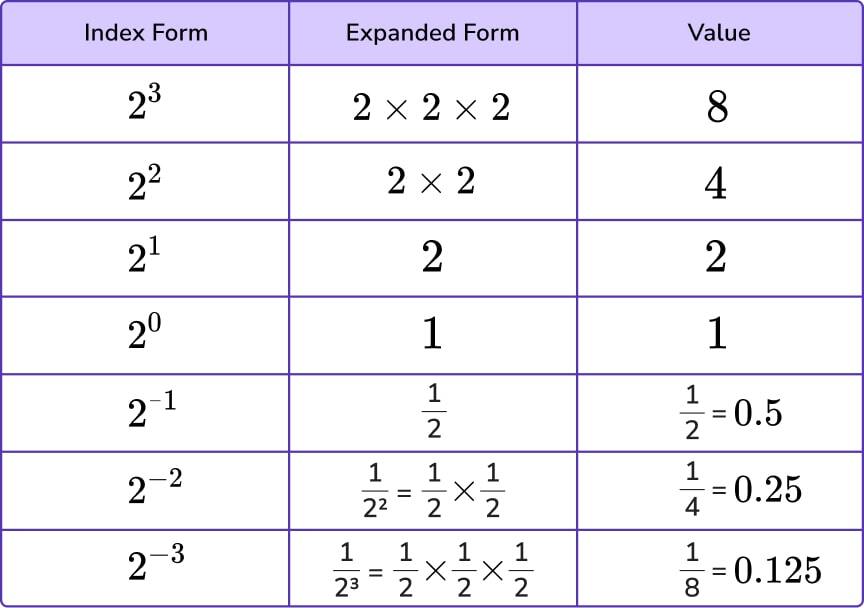
Moving up the rows we get 2 times larger per row.

Moving down the rows we get 2 times smaller per row.

Calculations with indices

In order to calculate with indices we need to be able to use the laws of indices in a variety of different ways. Let’s look at the different ways we can calculate with indices.

How to use the laws of indices

We can use the laws of indices to simplify expressions.

Explain how to use the laws of indices

Law 1: multiplying indices

When multiplying indices with the same base, add the powers.

\[a^{m} \times a^{n}=a^{m+n}\]

1 Add the powers.

2 Multiply any coefficients.

…………………………………………………………………………………………………………………………………………………….

Example

Simplify

\[4 a^{3} \times 7 a^{2}\]

This can be written as

\[4 a^{3} \times 7 a^{2}=4 \times a \times a \times a \times 7 \times a \times a\]

1 Add together the indices 3 and the 2.

\[3 + 2 = 5\]

2 Multiply 4 and 7 together.

\[4 \times 7 =28\]

So,

\[4 a^{3} \times 7 a^{2}=28 a^{5}\]

Law 2: dividing indices

When dividing indices with the same base, subtract the powers.

\[a^{m} \div a^{n}=a^{m-n}\]

Subtract the indices.
Divide any coefficients of the base number or letter.

…………………………………………………………………………………………………………………….………………………………

Example

Simplify

\[21 a^{9} \div 7 a^{2}\]

Subtract the indices 9 and 2.

\[9 – 2 = 7\]

Divide the coefficients 21 and 7.

\[21 ÷ 7 = 3\]

So,

\[21 a^{9} \div 7 a^{2}=3a^{7}\]

Law 3: brackets with indices

When there is a power outside the bracket multiply the powers.

\[(a^{m})^{n}=a^{m \times n}\]

Multiply the indices.
Raise all coefficients inside the bracket to the power outside the bracket.

Why does this work?

Let’s look at

\[(a^{3})^{4}\]

This algebraic expression has been raised to the power of 4, which means:

\[a^{3} \times a^{3} \times a^{3} \times a^{3}\]

We know when we multiply indices with the same base, we must add the powers.

\[a^{3} \times a^{3} \times a^{3} \times a^{3}=a^{12}\]

Is there a quicker way to work this out?

Simplifying a³ × a³ × a³ × a³ to a^3×4 we can work out the simplified answer is a¹².

\[(a^{3})^{4}=a^{3 \times 4}=a^{12}\]

When we have brackets and indices we can multiply the powers.

Brackets with indices examples

Example 1: no coefficient in front of base

Simplify and leave your answer in index form.

\[(a^{3})^{4}\]

Multiply the powers 3 and the 4.

\[3\times 4=12\]

So,

\[\left(a^{3}\right)^{4}=a^{12}\]

Example 2: coefficient inside bracket

Simplify and leave your answer in index form.

\[(10 a^{3})^{2}\]

Multiply the indices 3 and the 2.

\[3\times 2=6\]

Raise 10 to the power of 2.

\[10^{2}=100\]

So,

\[\left(10 a^{3}\right)^{2}=100 a^{6}\]

Example 3: negative indices

Simplify and leave your answer in index form.

\[(-4a^{-3})^{2}\]

Multiply the indices -3 and the 2.

\[-3\times 2=-6\]

Raise -4 to the power of 2.

\[(-4)^{2}=16\]

So,

\[\left(-4 a^{-3}\right)^{2}=16 a^{-6}\]

Law 4: power of 0

Any non-zero value raised to the power of 0 is equal to 1.

Example

Simplify

\[12a^{0}\]

\[= 12 (1) = 12\]

We can see that 12 × 1 = 12.

Multiplying anything by 1 leaves it unchanged, this is called the multiplicative identity.

So,

\[12 a^{0}=12\]

Law 5: negative indices

When the index is negative, put it over 1 and flip to make it positive.

\[a^{-m}=\frac{1}{a^{m}}\]

Put the term over 1.
Flip the fraction to make the index positive.
Simplify if necessary.

Example

Simplify

\[(2a)^{-3}\]

Notice how the index affects the entire bracket

Put the term over 1.

\[\frac{(2a)^{-3}}{1}\]

Flip and change the power -3 to +3.

\[\frac{1}{(2a)^{3}}\]

Simplify the denominator.

\[=\frac{1}{8a^{3}}\]

So,

\[(2 a)^{-3}=\frac{1}{8 a^{3}}\]

Law 6: fractional indices (H)

When the index is a fraction, the denominator is the root of the number or letter, then raise the answer to the power of the numerator.

\[x^{\frac{a}{b}}=(\sqrt[b]{x})^{a}\]

Use the denominator to find the root of the term
Raise the answer to the power of the numerator

Example

Evaluate

\[27^{\frac{2}{3}}\]

Use the denominator to find the cube root of the number or letter.

\[\sqrt[3]{27}=3\]

Raise the answer to the power of the numerator.

\[3^{2}=9\]

So,

\[27^{\frac{2}{3}}=9\]

Common misconceptions

The multiplication and division laws can only be used for terms with the same base

You cannot simplify

\[a^{4} \times b^{3}\]

as the bases are different

When a power is outside the bracket you must raise all terms inside the bracket by that power

E.g.

When we simplify

\[(4a)^{2}\]

We must remember to square both the 4 and the a. It is common to forget to square the 4.

\[(4 a)^{2}=4 a \times 4 a=4^{2} a^{2}=16 a^{2}\]

The brackets mean the entire term is squared.

Confusing integer and fractional powers

Raising a term to the power of 2 means we square it

E.g.

\[a^{2}=a \times a\]

Raising a term to the power of ½ means we find the square root of it

E.g.

\[a^{\frac{1}{2}}=\pm \sqrt{a}\]

Raising a term to the power of 3 means we cube it

E.g.

\[a^{3}=a \times a \times a\]

Raising a term to the power of ⅓ means we find the cube root of it

E.g.

\[a^{\frac{1}{3}}=\sqrt[3]{a}\]

Confusing positive and negative powers

We can have decimal, fractional, negative or positive integers.

Indices, powers or exponents

Indices can also be called powers or exponents.

Practice laws of indices questions

20 a^{8}

20 a^{-12}

20 a^{4}

20 a^{12}

We need to multiply the coefficients

4\times5=20

Since the base number is the same in each term, we can add the indices

6+(-2)=4

This means

4 a^{6} \times 5 a^{-2}=20 a^{4}

18 a^{11 b}

18 a^{28 b}

-18 a^{28 b}

-18 a^{11 b}

We need to multiply the coefficients

-3\times6=-18

Since the base number is the same in each term, we can add the indices

4b+7b=11b

This means

-3 a^{4 b} \times 6 a^{7 b}=-18 a^{11 b}

5 b^{2}

5 b^{5}

16 b^{5}

20 b^{5}

We need to multiply the coefficients

20\div4=5

Since the base number is the same in each term, we can subtract the indices

10-5=5

This means

20 b^{10} \div 4 b^{5}=5 b^{5}

7 a^{-5}

7 a^{11}

7 a^{5}

7 a^{-11}

We need to divide the coefficients

42\div6=7

Since the base number is the same in each term, we can subtract the indices

-3- \,-8=-3+8=5

This means

42a^{-3} \div 6 a^{-8}=7 a^{5}

36x^{2}

192x

36

192x^{2}

Anything raised to the power zero is $1$ , so

(32 x)^{0}=1

This means we have

1\times6^{2}=1\times36=36

125x^{-3}

125x^{3}

\frac{1}{125x^{-3}}

\frac{1}{125x^{3}}

The negative index number indicates we need the reciprocal of

(5x)^{3}

Since

5x^{3}=5x\times5x\times5x=125x^{3}

We have

(5 x)^{-3}=\frac{1}{125 x^{3}}

2b

\frac{3}{2b}

\frac{6}{b^{4}}

\frac{1296}{b^{4}}

The negative index number indicates we need the reciprocal of

b^{4}

The index number does not affect the $6$ , hence

6 b^{-4}=\frac{6}{b^{4}}

8

16

512

\frac{128}{3}

The index number is telling us to square the cube root, so

64^{\frac{2}{3}}=(\sqrt[3]{64})^{2}=4^{2}=16

8

\frac{1}{4}

4

-8

The index number is telling us to find the reciprocal of the square root, so

\begin{aligned} &16^{-\frac{1}{2}}\\ &=\frac{1}{16^{\frac{1}{2}}}\\ &=\frac{1}{\sqrt{16}}\\ &=\frac{1}{4} \end{aligned}

Laws of indices GCSE questions

1. Simplify

\frac{p^{7}}{p^{3}}

(1 mark)

Show answer

$p^{4}$

(1)

2. Simplify

6 h^{3} m^{6} \times 4 h^{4} m^{5}

(2 marks)

Show answer

$h^{7} \text { or } m^{11}$ seen (evidence of adding powers)

(1)

$24 h^{7} m^{11}$

(1)

3. Simplify

$\frac{12 x^{5} y^{7}}{3 x^{2} y}$

(2 marks)

Show answer

$x^{3} \text { or } y^{6}$ seen (evidence of subtracting powers)

(1)

$4 x^{3} y^{6}$

(1)

Learning checklist

You have now learned how to:

Simplify expressions involving the laws of indices

Calculate with roots, and with integer and fractional indices

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.