Geometric sequences

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Arithmetic Substitution Arithmetic sequences

This topic is relevant for:

GCSE Maths Algebra Sequences

Geometric Sequences

Here we will learn what a geometric sequence is, how to continue a geometric sequence, how to find missing terms in a geometric sequence, and how to generate a geometric sequence.

At the end, you’ll find geometric sequence worksheets based on Edexcel, AQA, and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a geometric sequence?

A geometric sequence (geometric progression) is an ordered set of numbers that progresses by multiplying or dividing each term by a common ratio.

If we multiply or divide by the same number each time to make the sequence, it is a geometric sequence.

The common ratio is the same for any two consecutive terms in the same sequence.

Here are a few examples,

First Term	Term-to-Term Rule	First $5$ Terms
$3$	Multiply by $3$	$3, 9, 27, 81, 243, ...$
$5$	Multiply by $2$	$5, 10, 20, 40, 80, ...$
$-12$	Divide by $2$	$-12, -6, -3, -1.5, -0.75, ...$
$0.8$	Multiply by $5$	$0.8, 4, 20, 100, 500, ...$
$\frac{1}{2}$	Divide by $4$	$\frac{1}{2}, \; \frac{1}{8}, \; \frac{1}{32}, \; \frac{1}{128}, \; \frac{1}{512} \ldots$

What are geometric sequences?

Geometric sequence formula

The geometric sequence formula is,

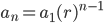
Where,

$\pmb{ a_{n} }$ is the $n^{th}$ term (general term),

$\pmb{ a_{1} }$ is the first term,

$\pmb{ n }$ is the term position,

and $\pmb{ r }$ is the common ratio.

We get the geometric sequence formula by looking at the following example,

We can see the common ratio $(r)$ is $2$ , so $r = 2$ .

$a_{1}$ is the first term which is $5$ ,

$a_{2}$ is the second term which is $10$ ,

and $a_{3}$ is the third term which is $20$ etc.

However we can write this using the common difference of $2$ ,

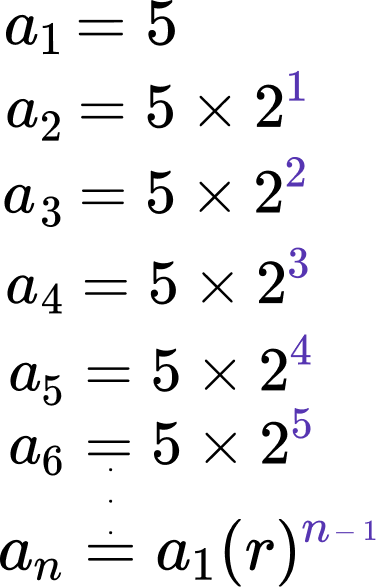
Related lessons on sequences

Geometric sequences is part of our series of lessons to support revision on sequences. You may find it helpful to start with the main sequences lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

How to continue a geometric sequence

To continue a geometric sequence, you need to calculate the common ratio. This is the factor that is used to multiply one term to get the next term. To calculate the common ratio and continue a geometric sequence you need to:

Take two consecutive terms from the sequence.
Divide the second term by the first term to find the common ratio $r$ .
Multiply the last term in the sequence by the common ratio to find the next term. Repeat for each new term.

Explain how to continue a geometric sequence

Geometric sequences worksheet

Get your free geometric sequences worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Geometric sequences worksheet

Get your free geometric sequences worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Continuing a geometric sequence examples

Example 1: continuing a geometric sequence

Calculate the next three terms for the geometric progression $1, 2, 4, 8, 16,$ …

Take two consecutive terms from the sequence.

Here we will take the numbers $4$ and $8$ .

2 Divide the second term by the first term to find the value of the common ratio, $r$ .

\begin{aligned} r&=8 \div 4 \\\\ r&=2 \end{aligned}

3 Multiply the last term in the sequence by the common ratio to find the next term. Repeat for each new term.

\begin{aligned} 16 \times 2&=32 \\\\ 32 \times 2&=64 \\\\ 64 \times 2&=128 \end{aligned}

The next three terms in the sequence are $32, 64,$ and $128$ .

Example 2: continuing a geometric sequence with negative numbers

Calculate the next three terms for the sequence $-2, -10, -50, -250, -1250, \dots$

Take two consecutive terms from the sequence.

Here we will take the numbers $-10$ and $-50$ .

Divide the second term by the first term to find the common ratio, $r.$

r=-50 \div -10

r=5

Multiply the last term in the sequence by the common ratio to find the next term. Repeat for each new term.

-1250 \times 5=-6250

-6250 \times 5=-31250

-31250 \times 5=-156250

The next three terms are $-6250, -31250,$ and $-156250.$

Example 3: continuing a geometric sequence with decimals

Calculate the next three terms for the sequence $100, 10, 1, 0.1, 0.01,$ …

Take two consecutive terms from the sequence.

Here we will take the numbers $0.1$ and $0.01$ .

Divide the second term by the first term to find the common ratio, $r$ .

\begin{aligned} r&=0.01 \div 0.1 \\\\ r&=0.1 \end{aligned}

Multiply the last term in the sequence by the common ratio to find the next term. Repeat for each new term.

\begin{aligned} 0.01 \times 0.1&=0.001\\\\ 0.001 \times 0.1&=0.0001\\\\ 0.0001 \times 0.1&=0.00001\\\\ \end{aligned}

The next three terms in the sequence are $0.001, 0.0001,$ and $0.00001.$

Example 4: continuing a geometric sequence involving fractions

Calculate the next three terms for the sequence

10, \quad 5, \quad 2\frac{1}{2}, \quad 1 \frac{1}{4}, \quad \frac{5}{8}, ...

Take two consecutive terms from the sequence.

Here we will take the numbers $5$ and $2\frac{1}{2}$ .

Divide the second term by the first term to find the common ratio, $r.$

\begin{aligned} r&=2 \frac{1}{2} \div 5\\\\ r&= \frac {1}{2} \end{aligned}

Multiply the last term in the sequence by the common ratio to find the next term. Repeat for each new term.

\begin{aligned} \frac{5}{8} \times \frac{1}{2}&=\frac{5}{16} \\\\ \frac{5}{16} \times \frac{1}{2}&=\frac{5}{32} \\\\ \frac{5}{32} \times \frac{1}{2}&=\frac{5}{64} \end{aligned}

The next three terms are

$\frac{5}{16}, \frac{5}{32},$ and $\frac{5}{64}$ .

Geometric sequence practice questions – continue the sequence

1000, 5000, 10000

950, 1400, 1850

5000, 50000, 500000

550, 555, 560

Choose two consecutive terms. For example, $5$ and $50$ .

Common ratio,

50\div 5=10

500 \times 10=5000, 5000 \times 10=50000, 50000 \times 10=500000

50, 100, 200

125, 625, 3125

50, 1000, 20000

12.5, 6.25, 3.125

Choose two consecutive terms. For example, $5$ and $25$ .

Common ratio,

25\div 5=5

25 \times 5=125, 125 \times 5=625, 625 \times 5=3125

243, 729, 2187

-243, -729, -2187

243, -729, 2187

-27, -9, -3

Choose two consecutive terms. For example, $-27$ and $-9$ .

Common ratio,

-27\div -9=3

-81 \times 3=-243, -243 \times 3=-729, -729 \times 3=-2187

0.625, 0.15625, 0.0390625

1.25, 0.625, 0.3125

10, 40, 160

0.25, 0.025, 0.0025

Choose two consecutive terms. For example, $40$ and $10$ .

Common ratio,

10\div 40=\frac{1}{4} \text{ or } 0.25

2.5 \times 0.25=0.625, 0.625 \times 0.25=0.15625, 0.15625 \times 0.25=0.0390625

\frac{12}{9}, \frac{36}{9}, \frac{108}{9}

\frac{12}{27}, \frac{36}{81}, \frac{108}{243}

\frac{4}{12}, \frac{4}{15}, \frac{4}{18}

\frac{4}{27}, \frac{4}{81}, \frac{4}{243}

Choose two consecutive terms. For example, $12$ and $4$ .

Common ratio,

4\div 12=\frac{1}{3}

\frac{4}{9} \times \frac{1}{3}=\frac{4}{27}, \frac{4}{27} \times \frac{1}{3}=\frac{4}{81}, \frac{4}{81} \times \frac{1}{3}=\frac{4}{243}

1, 1, 1

-1, -1, -1

1, -1, 1

-1, 1, -1

Choose two consecutive terms. For example, $-1$ and $1$ .

Common ratio,

-1\div 1=-1

1 \times -1=-1, -1 \times -1=1, 1 \times -1=-1

How to find missing numbers in a geometric sequence

The common ratio can be used to find missing numbers in a geometric sequence. To find missing numbers in a geometric sequence you need to:

Calculate the common ratio between two consecutive terms.
Multiply the term before any missing value by the common ratio.
Divide the term after any missing value by the common ratio.

Repeat Steps 2 and 3 until all missing values are calculated. You may only need to use Step 2 or 3 depending on what terms you have been given.

Explain how to find missing numbers in a geometric sequence

Finding missing numbers in a geometric sequence examples

Example 5: find the missing numbers in the geometric sequence

Fill in the missing terms in the sequence $7, 14, \dots, \dots,112$ .

Calculate the common ratio between two consecutive terms.

\begin{aligned} r&=14 \div 7 \\\\ r&=2 \end{aligned}

Multiply the term before any missing value by the common ratio.

14 \times 2=28

Divide the term after any missing value by the common ratio.

112 \div 2 = 56

The missing terms are $28$ and $56$ .

Note: Here, you could repeat Step 2 by using $28 \times 2 = 56.$

Example 6: find the missing numbers in a geometric sequence including decimals

Find the missing values in the sequence $0.4, \dots, ..., 137.2, 960.4.$

Calculate the common ratio between two consecutive terms.

\begin{aligned} r&=960.4 \div 137.2 \\\\ r&=7 \end{aligned}

Multiply the term before any missing value by the common ratio.

0.4 \times 7 = 2.8

Divide the term after any missing value by the common ratio.

137.2 \div 7 = 19.6

The missing terms are $2.8$ and $19.6$ .

Example 7: find the missing numbers in a geometric sequence when there are multiple consecutive terms missing

Find the missing values in the sequence, $-4, ..., \dots, -108,...$

Calculate the common ratio between two consecutive terms.

First, we need to find the factor between the two terms, $-108 \div -4 = 27$ .

To get from $-108$ to $-4$ , we jump $3$ terms.

This means that $-4$ has been multiplied by the common ratio three times or $-4 \times r \times r \times r = -4r^3$ .

$\begin{aligned} r^{3}&=27\\\\ r&=3 \end{aligned}$

Multiply the term before any missing value by the common ratio.

\begin{aligned} -4 \times 3&=-12 \\\\ -12 \times 3&=-36 \\\\ -36 \times 3&=-108 \\\\ -108 \times 3&=-324 \end{aligned}

Note: Term $-108$ is already given.

The missing terms are $-12, -36,$ and $-324.$

Divide the term after any missing value by the common ratio.

We don’t need to complete this step.

Example 8: find the missing numbers in a geometric sequence including mixed numbers

Find the missing values in the sequence

…, 4 \frac{1}{2}, \quad 13 \frac{1}{2},\quad ... , \quad...

Calculate the common ratio between two consecutive terms.

\begin{aligned} r&=13 \frac{1}{2} \div 4 \frac{1}{2}\\\\ r &=\frac{27}{2} \div \frac{9}{2}\\\\ r &=\frac{27}{2} \times \frac{2}{9}\\\\ r &=3 \end{aligned}

Multiply the term before any missing value by the common ratio.

13 \frac{1}{2} \times 3=40 \frac{1}{2}

Repeat this step to find the next term.

$40 \frac{1}{2} \times 3=121 \frac{1}{2}$

Divide the term after any missing value by the common ratio.

4 \frac{1}{2} \div 3=1 \frac{1}{2}

The missing terms in the sequence are

$1 \frac{1}{2}, 40 \frac{1}{2},$ and $121 \frac{1}{2}$ .

Geometric sequence practice questions – find missing numbers

1, 0.2

1, 0.25

1, 0.1

1, 0

Choose two consecutive terms. For example, $4$ and $2$ .

Common ratio,

2\div 4=0.5

2 \times 0.5=1, 0.5 \times 0.5=0.25

-175, -875

175, 875

-4375, -546875

1481.7, 2928.3

Choose two consecutive terms. For example, $-7$ and $-35$ .

Common ratio,

-35\div -7=5

-35 \times 5=-175, -175 \times 5=-875

0.2, 0.067

1.2, 2.4

0.12, 0.24

0.3, 0.15

Choose two consecutive terms. For example, $0.075$ and $0.0375$ .

Common ratio,

0.0375\div 0.075=0.5

-35 \times 5=-175, -175 \times 5=-875

\frac{11}{320}, \frac{11}{1280}

\frac{44}{80}, \frac{176}{80}

\frac{44}{320}, \frac{176}{1280}

\frac{11}{140}, \frac{11}{200}

Choose two consecutive terms. For example, $\frac{11}{20}$ and $\frac{11}{80}$ .

Common ratio,

\frac{11}{80} \div \frac{11}{20}=\frac{11}{80} \times \frac{20}{11}=\frac{1}{4}

\frac{11}{80} \times \frac{1}{4}=\frac{11}{320}, \frac{11}{320} \times \frac{1}{4}=\frac{11}{1280}

10, 17

9, 18

6, 12

12, 18

$3$ has been multiplied by the common ratio, $r,$ three times to get $24.$

Therefore,

$3 \times r \times r \times r=24 \text{ or } 3r^{3}=24$ .

Solving the equation,

\begin{aligned} 3r^{3}&=24\\ r^{3}&=8\\ r&=2 \end{aligned}

3 \times 2=6, 6 \times 2=12

\frac{550}{9}, \frac{290}{9}

9, 3

30, 10

45, \frac{45}{2}

$90$ has been multiplied by the common ratio, $r,$ three times to get $\frac{10}{3}.$

Therefore,

$90 \times r \times r \times r=\frac{10}{3} \text{ or } 90r^{3}=\frac{10}{3}$ .

Solving the equation,

\begin{aligned} 90r^{3}&=\frac{10}{3}\\ r^{3}&=\frac{10}{3} \div 90\\ r^{3} = \frac{1}{27} r&=\frac{1}{3} \end{aligned}

90 \times \frac{1}{3}=30, 30 \times \frac{1}{3}=10

How to generate a geometric sequence

In order to generate a geometric sequence, we need to know the $n^{th}$ term. Using $a$ as the first term of the sequence, $r$ as the common ratio and $n$ to represent the position of the term, the $n^{th}$ term of a geometric sequence is written as $ar^{n-1}.$

Once we know the first term and the common ratio, we can work out any number of terms in the sequence.

The first term is found when $n=1$ , the second term when $n=2$ , the third term when $n=3$ and so on.

To generate a geometric sequence you need to:

Substitute $n=1$ into the $n^{th}$ term to calculate the first term.
Substitute $n=2$ into the $n^{th}$ term to calculate the second term.
Continue to substitute values for $n$ until all the required terms of the sequence are calculated.

Explain how to generate a geometric sequence

Generating a geometric sequence examples

Example 9: generate a geometric sequence using the n^th term

Generate the first $5$ terms of the sequence $4^{n-1}$ .

Substitute $n = 1$ into the $n^{th}$ term to calculate the first term.

When $n = 1,\quad 4^{1-1} = 4^{0} = 1$ .

Substitute $n = 2$ into the $n^{th}$ term to calculate the second term.

When $n = 2,\quad 4^{2-1 }= 4^{1} = 4$ .

Continue to substitute values for $n$ until all the required terms of the sequence are calculated.

When $n=3, \quad 4^{3-1}=4^{2}=16$ .

When $n=4, \quad 4^{4-1}=4^{3}=64$ .

When $n=5, \quad 4^{5-1}=4^{4}=256$ .

The first $5$ terms of the sequence are $1, 4, 16, 64, 256.$

Example 10: generate a geometric sequence using a table

Complete the table for the first $5$ terms of the arithmetic sequence $6 \times 2^{n-1}.$

n	1	2	3	4	5
2^n-1
6 × 2^n-1

Substitute $n = 1$ into the $n^{th}$ term to calculate the first term.

n	1	2	3	4	5
2^n-1	2⁰ = 1
6 × 2^n-1	6

Substitute $n = 2$ into the $n^{th}$ term to calculate the second term.

n	1	2	3	4	5
2^n-1	2⁰ = 1	2¹ = 2
6 × 2^n-1	6	12

Continue to substitute values for $n$ until all the required terms of the sequence are calculated.

n	1	2	3	4	5
2^n-1	2⁰ = 1	2¹ = 2	2² = 4	2³ = 8	2⁴ = 16
6 × 2^n-1	6	12	24	48	96

Example 11: generate larger terms in a geometric sequence

A geometric sequence has the $n^{th}$ term $\left(\frac{1}{2}\right)^{n}$ .

Calculate the $1^{st}, 2^{nd}, 10^{th}$ and $12^{th}$ terms in the sequence. Express your answers as fractions.

Substitute $n = 1$ into the $n^{th}$ term to calculate the first term.

When $n=1,\quad \left(\frac{1}{2}\right)^{1}=\frac{1}{2}$ .

Substitute $n = 2$ into the $n^{th}$ term to calculate the second term.

When $n=2, \quad \left(\frac{1}{2}\right)^{2}=\frac{1}{4}$ .

Continue to substitute values for $n$ until all the required terms of the sequence are calculated.

When $n=10,\quad \left(\frac{1}{2}\right)^{10}=\frac{1}{1024}$ .

When $n=12,\quad \left(\frac{1}{2}\right)^{12}=\frac{1}{4096}$ .

The unknown terms are

$1, \frac{1}{4}, \frac{1}{1024},$ and $\frac{1}{4096}$ .

Example 12: generate a geometric sequence with a negative common ratio

Generate the first $5$ terms of the geometric sequence $2(- 3)^{n-1}$ .

Substitute $n = 1$ into the $n^{th}$ term to calculate the first term.

When $n=1, \quad 2(-3)^{n-1}=2(-3)^{1-1}=2(-3)^{0}=2 \times 1=2$ .

Substitute $n = 2$ into the $n^{th}$ term to calculate the second term.

When $n=2,\quad 2(-3)^{n-1}=2(-3)^{2-1}=2(-3)^{1}=2 \times-3=-6$ .

Continue to substitute values for $n$ until all the required terms of the sequence are calculated.

When $n=3, \quad 2(-3)^{n-1}=2(-3)^{3-1}=2(-3)^{2}=2 \times 9=18$ .

When $n=4, \quad 2(-3)^{n-1}=2(-3)^{4-1}=2(-3)^{3}=2 \times-27=-54$ .

When $n=5, \quad 2(-3)^{n-1}=2(-3)^{5-1}=2(-3)^{4}=2 \times 81=162$ .

The first $5$ terms of the sequence are $2, -6, 18, -54,$ and $162$ .

Geometric sequence practice questions – generate a sequence

10, 100, 1000, 10000, 100000

1, 10, 100, 1000, 10000

10, 20, 30, 40, 50

100, 1000, 10000, 100000, 1000000

When $n=1, 10^{1}=10$ .

When $n=2, 10^{2}=100$ .

When $n=3, 10^{3}=1000$ .

When $n=4, 10^{4}=10000$ .

When $n=5, 10^{5}=100000$ .

5, 25, 125, 625, 3125

0.2, 1, 5, 25, 125

625, 125, 25, 5, 1

1, 5, 25, 125, 625

When $n=1, 5^{1-1}=5^{0}=1$ .

When $n=2, 5^{2-1}=5^{1}=5$ .

When $n=3, 5^{3-1}=5^{2}=25$ .

When $n=4, 5^{4-1}=5^{3}=125$ .

When $n=5, 5^{5-1}=5^{4}=625$ .

1, 3, 9, 27, 81

1, 12, 144, 1728, 20736

4, 12, 36, 108, 324

12, 36, 108, 324, 972

When $n=1, 4 \times 3^{1-1}=4 \times 3^{0}=4$ .

When $n=2, 4 \times 3^{2-1}=4 \times 3^{1}=12$ .

When $n=3, 4 \times 3^{3-1}=4 \times 3^{2}=36$ .

When $n=4, 4 \times 3^{4-1}=4 \times 3^{3}=108$ .

When $n=5, 4 \times 3^{5-1}=4 \times 3^{4}=324$ .

\frac{1}{2}, 1 \frac{1}{2}, 4 \frac{1}{2}, 13 \frac{1}{2}, 40 \frac{1}{2}

\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}

\frac{1}{6}, \frac{1}{2}, 1 \frac{1}{2}, 4 \frac{1}{2}, 13 \frac{1}{2}

\frac{1}{6}, 1 \frac{1}{2}, 4 \frac{1}{2}, 13 \frac{1}{2}, 40 \frac{1}{2}

When $n=1, \frac{3^1}{6}= \frac{1}{2}$ .

When $n=2, \frac{3^2}{6}= \frac{9}{6} = 1 \frac{1}{2}$ .

When $n=3, \frac{3^3}{6}= \frac{27}{6} = 4 \frac{1}{2}$ .

When $n=4, \frac{3^4}{6}= \frac{81}{6} = 13 \frac{1}{2}$ .

When $n=5, \frac{3^5}{6}= \frac{243}{6} = 40 \frac{1}{2}$ .

2, 4, 8, 16

2, 8, 1024, 32768

1, 4, 512, 16384

4, 16, 2048, 65536

When $n=1, 2^{1}= 2$ .

When $n=3, 2^{3}= 8$ .

When $n=10, 2^{10}= 1024$ .

When $n=15, 2^{15}= 32768$ .

3, -15, 75, -375, 1875

1, -5, 25, -125, 625

1, -225, 3375, -50625, 759375

-15, 75, -375, 1875, -9375

When $n=1, 3 \times (-5)^{1-1} = 3 \times (-5)^{0} = 3$ .

When $n=2, 3 \times (-5)^{2-1} = 3 \times (-5)^{1} = -15$ .

When $n=3, 3 \times (-5)^{3-1} = 3 \times (-5)^{2} = 75$ .

When $n=4, 3 \times (-5)^{4-1} = 3 \times (-5)^{3} = -375$ .

When $n=5, 3 \times (-5)^{5-1} = 3 \times (-5)^{4} = 1875$ .

Geometric sequences GCSE exam questions

1. Which sequence is a geometric progression?

$1, 3, 5, 7, 9,…. \quad \quad \quad 1, 3, 9, 27, 81, …..$

$1, 3, 6, 10, 15, …. \quad \quad 1, 0.6, 0.2, -0.2, -0.6,….$

(1 mark)

Show answer

$1, 3, 9, 27, 81, \dots..$

(1)

2. Here is a geometric progression,

$1, -5, 25, \dots., 625, \dots$

(a) Find the common ratio.

(b) Work out the fourth term of the sequence.

(3 marks)

Show answer

(a)

$25 \div -5 = – 5$

Common ratio $= -5$

(1)

(b)

$25 \times -5$

(1)

$= -125$

(1)

3. A scientist is studying a type of bacteria. The number of bacteria over the first four days is shown below.

Day 1	Day 2	Day 3	Day 4
60	180	540	1620

How many bacteria will there be on day 7?

(3 marks)

Show answer

$180 \div 60 = 3$

(1)

$1620 \times 3 \times 3 \times 3$

(1)

$43740$

(1)

Common misconceptions

Mixing up the common ratio with the common difference for arithmetic sequences

Although these two phrases are similar, each successive term in a geometric sequence of numbers is calculated by multiplying the previous term by a common ratio and not by adding a common difference.

A negative value for r means that all terms in the sequence are negative

This is not always the case as when $r$ is raised to an even power, the solution is always positive.

The first term in a geometric sequence

The first term is $a$ . With $ar^{n-1}$ , the first term would occur when $n = 1$ and so the power of $r$ would be equal to $0$ . Anything to the power of $0$ is equal to $1$ , leaving $a$ as the first term in the sequence. This is usually mistaken when $a = 1$ as it is not clearly noted in the question for example, $2^{n-1}$ is the same as $1 \times 2^{n-1}$ .

Incorrect simplifying of the n^th term

For example, $6 \times 3^{n-1}$ is incorrectly simplified to $18^{n-1}$ as $6 \times 3 = 18$ .

The difference between an arithmetic and a geometric sequence

Arithmetic sequences are formed by adding or subtracting the same number. Geometric sequences are formed by multiplying or dividing the same number.

Learning checklist

You have now learned how to:

Recognise geometric sequences

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.