Why SSDD Problems Are Such An Effective Tool To Teach Problem Solving At KS3 & KS4
SSDD problems, or Same Surface Different Depth problems, offer a world of opportunities to develop your students’ critical thinking skills. In this article, we explain what they are and how to use them, provide you with downloadable examples and explain why they are such an effective tool. We also guide you step by step to develop your own SSDD problems – including a downloadable template!
What are SSDD problems?
SSDD stands for Same Surface, Different Depth (or same surface different deep). The idea behind them is to provide a set of questions that look the same and use the same mathematical hook but each question requires a different mathematical process to be solved.
The idea was introduced in 2014 by maths teacher and author Craig Barton. SSDD problems have gained popularity among maths teachers as an effective way to ensure students engage carefully with questions and what they are being asked to do, rather than diving in on autopilot without a solid understanding of what the question is asking from them.
– not only angles!
Think about the image of a regular pentagon. As an experienced mathematician or teacher, you may be able to consider a large number of different mathematical concepts that can be drawn from this singular image. However, for students revising for an exam, they may rely on their knowledge and experience thus far and automatically start thinking about angles in polygons – but the question could be about pythagoras’ theorem, trigonometry, area, perimeter, surds, solving equations, graphs…
This is where SSDD problems can help! They train students to read and engage with questions more carefully.
Exemplar Same Surface Different Depth Questions
Download all of the SSDD problem examples included in this blog and more. Includes answers in a printable file.
Download Free Now!What are the different types of SSDD problems?
When searching for SSDD problems, you may think that the idea behind them all is the same. However, there are different ways of producing SSDD problems.
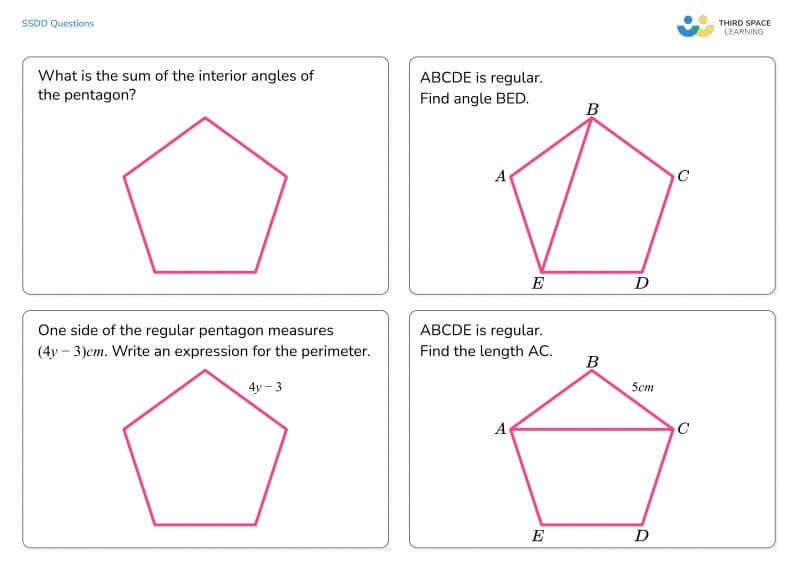
Same image, different questions (by content domain)
We can have a set of questions that use the same image but ask different questions by content domain.
Here, each question on the surface is about a regular pentagon, but looking carefully we can see that there are different mathematical ideas required to solve each question.
Answers are included in our downloadable, printable resource.
One question wants the sum of the angles to be found, one wants an angle between a diagonal and a side, one requires an algebraic relationship for the perimeter and one wants a length.
Same image, different questions (by cognitive domain)
But on another set of maths problems with the same surface image, we have 4 questions all about area but each requires a different level of thinking.
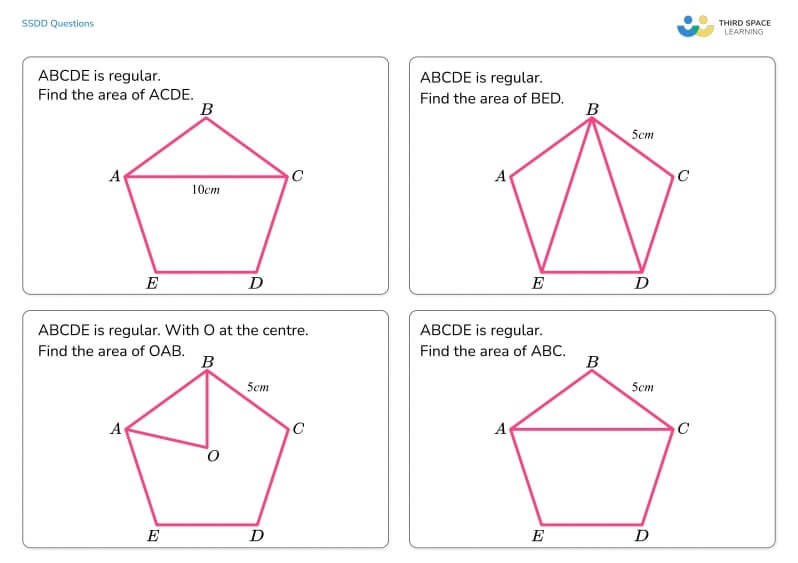
Answers are included in our downloadable resource.
Same structure to a problem with different meanings
Another type of SSDD questions could just focus on small changes to the language used in mathematical problems.
The difference between “20% of £340” and “20% off £340” is one that can cause many issues to students attempting different questions about percentages and fractions.
Similarly, with compound interest problems, if an investment made £400 compound interest – that is very different to an amount being worth £400 after receiving compound interest.
When thinking about enlarging a shape, using the same scale factor but applying it to lengths or areas or volumes produces very different answers.

Meet Skye, the voice-based AI tutor making maths success possible for every student.
Built by teachers and maths experts, Skye uses the same pedagogy, curriculum and lesson structure as our traditional tutoring.
But, with more flexibility and a lower cost, schools can scale online maths tutoring to support every student who needs it.
Watch Skye in actionWhy are SSDD problems so effective?
SSDD problems are an effective tool for teachers to introduce because of the following reasons:
- Spaced retrieval practice – While working on one topic, you can use SSDD problems to bring in aspects of other topics that students have studied previously, requiring students to retrieve past learning and, in turn, enhance their long term memory.
For example, while teaching perimeter to your class, you could give your students a set of SSDD problems based around the perimeter of a shape but also bring in aspects of algebra, area, fraction or decimal arithmetic. - Discriminative contrast – Presenting a set of questions which, on the surface, all look the same, forces students to look more deeply at each question and ask themselves “What’s the same? What’s different?”. This will make them think more carefully about how they will solve each problem.
- Attention attenuation – As mentioned earlier, we do not want students to get used to engaging autopilot to solve a series of questions all on the same topic.
SSDD problems force them to slow down in a good way and realise they may need to approach problems with a different method. They can also stop a student applying a newly learned skill on every new problem they see. For example, a student recently learns the cosine rule and then on a different day, tries to apply it on every question involving a triangle.
How to use SSDD problems
SSDD problems lend themselves very well to being introduced after a core skill has been taught, as part of the consolidation process. They can then be used for retrieval practice as starter activities or homework tasks.
They are suitable for KS3 maths problem solving and beyond.
It is important that each set of SSDD problems is chosen carefully for the task required. Some of the required knowledge from other areas of mathematics so the sequencing of topics taught will need to be considered. Many schools are building SSDD problems into their schemes of learning for primary and secondary mathematics lessons.
SSDD problems are also an excellent addition to a revision programme in the build up to GCSE maths exams. Reviews of topics followed by batches of related SSDD problems would help students with their analytical and maths problem solving skills.
Past exam paper questions could be used to create some SSDD problems. By removing some aspects of the question, you can ask learners to think about the different questions that could be asked around a concept.
How to create your own SSDD problems
Before creating your own SSDD problems, take a look at the many examples available online, in our downloadable resource and on Craig Barton’s website.
It’s also a good idea to use existing problem solving questions that can be adapted to SSDD problems.
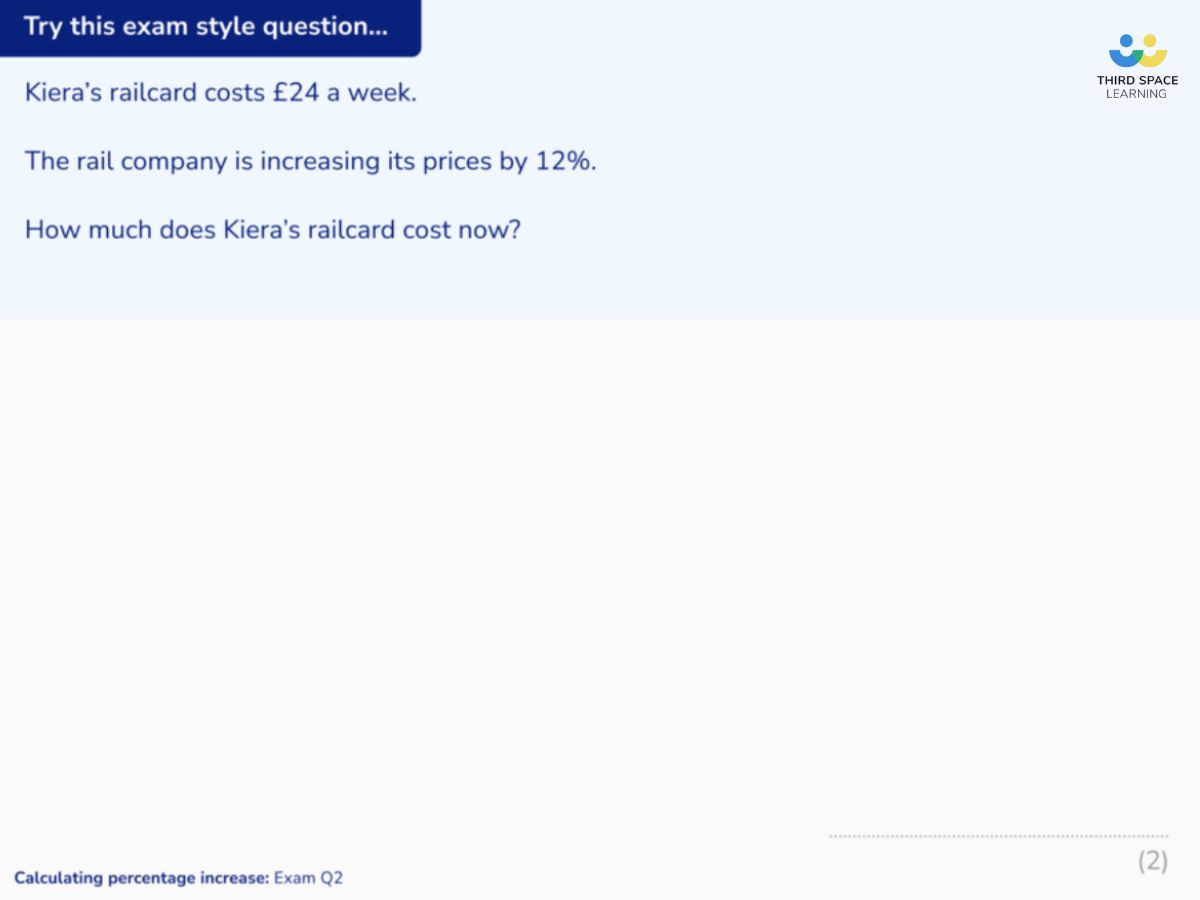
to create your own SSDD problems,
such as this question taken from our online one to one maths tutoring GCSE programme.
Creating your own SSDD problems is a two-step process:
i) Identify a core surface theme.
Think of a topic you are planning to teach in the future which may have links to other areas of mathematics. This could be an isosceles triangle, a fraction, decimal or percentage, a list of negative numbers or prime numbers, a statistical graph or table, or it could be an algebraic expression.
ii) Consider the different deep structures that you would like to embed.
Remember that there are multiple ways a set of SSDD problems could be constructed. Do you want every question to focus on a main key topic or do you want the task to be retrieving learning from the past?
SSDD problem creation step by step
Let’s build an SSDD problem together step by step.
We will use this quadratic graph as our “Same Surface”.
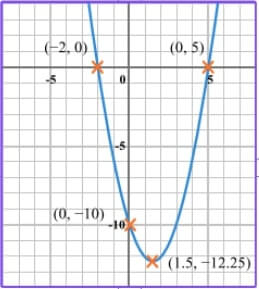
We can put this at the centre of an SSDD problems template with our first problem. This problem asks the student to find the equation of the quadratic.
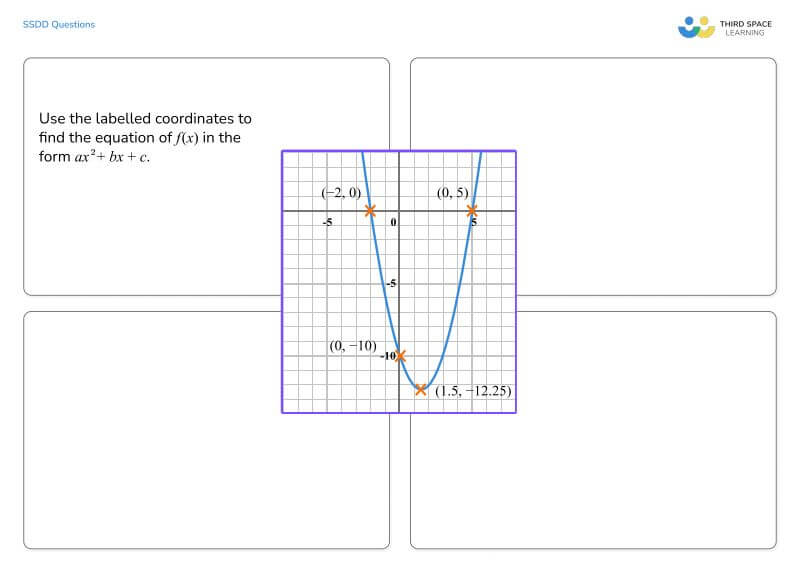
to help you develop your own SSDD problems.
We can then think about other mathematical ideas that could have this graph at the core.
For this graph, we’ve selected questions using the following concepts:
- finding gradients using tangents;
- estimating areas using trapeziums;
- locating coordinates after transformations.
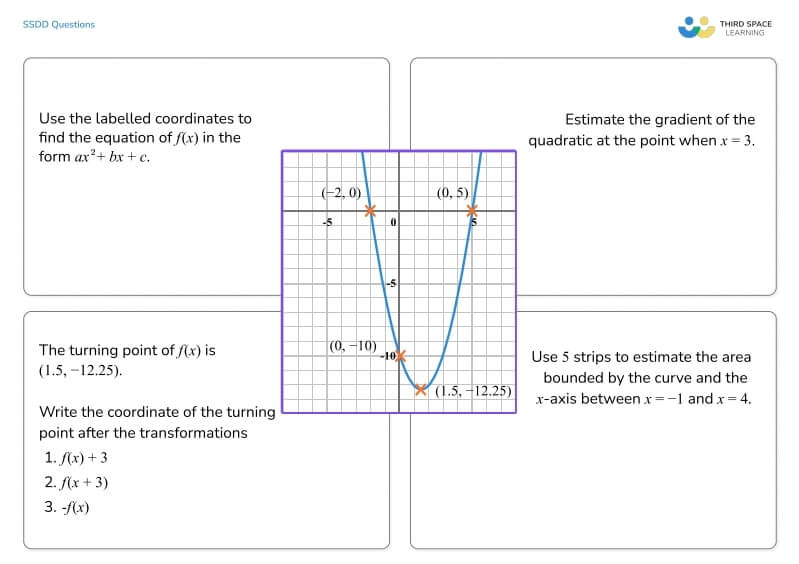
This is just one way this quadratic graph could be turned into an SSDD problem.
Alternatively, the same core diagram can be used and every question could be about finding the equation, but the information provided could change, as below:
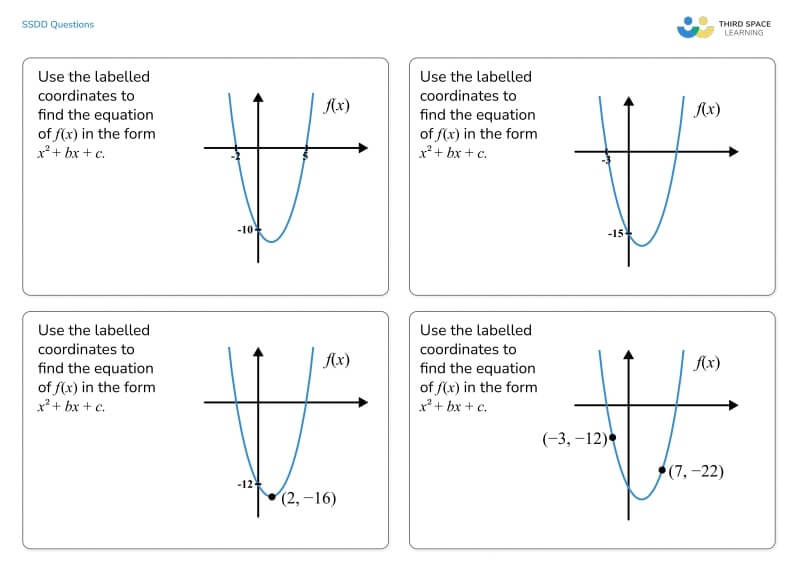
Even though it appears that each problem is the same, learners will have to think about how to use the labelled coordinates to find the equation. Each one will involve a different level of skill. This particular SSDD problem could be used for GCSE maths students or even A level maths students.
What is important is that each set of SSDD problems encourages deep thought and hits the following criteria:
- Spaced retrieval practice – Does it force students to recall past learning?
- Discriminative contrast – Can they find similarities and differences?
- Attention attenuation – Will the problems stop learners from engaging autopilot?
Example SSDD problems
Our downloadable resource includes all of the SSDD problem examples included in this blog and more, including their answers, in an easy to print PDF file.
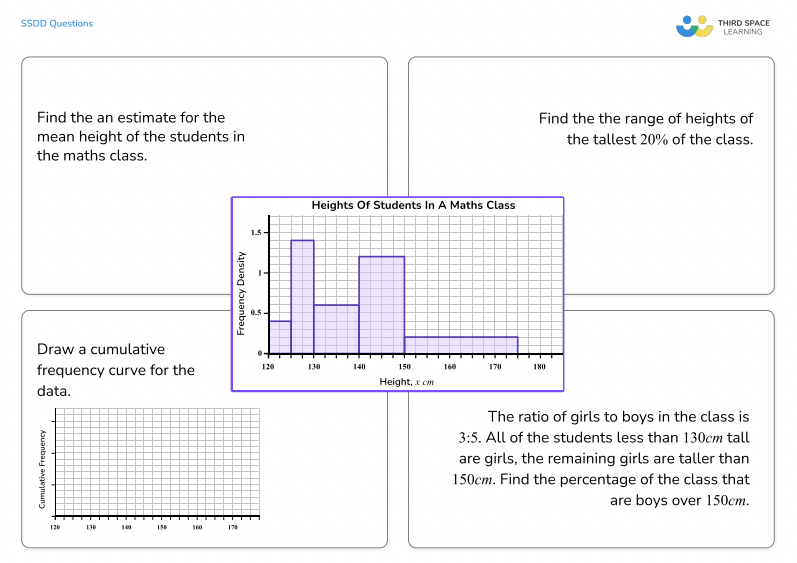

3 tips for teachers: SSDD problems
1. It is important that your students are confident tackling problem solving questions. Strengthen their skills using the problems below:
2. If you feel your class needs a little extra support to begin with, you could provide them with some scaffolding for each problem – maybe just some extra questions or a list of hints of what to look at.
For example, start with just two problems side by side and ask the class to write down a list of the things which are the same, and things that are different.
3. A nice starter activity is to get students to develop their own idea for SSDD problems by giving them an image of the “Same Surface” and asking them to come up with as many questions as possible related to that image. Students will need to be familiar with answering these before they can create their own!
For example, you could provide them with a set of coordinates.
- Can they find a straight line that goes through that point?
- Can they find a pair of simultaneous equations with that coordinate as the solution?
- Can they find a list of 8 coordinates so that the mean averages of the x-values and the mean average of the y-values is that point?
Once you and your pupils are confident working with SSDD problems, they can easily be embedded into your starter activities, exit tickets, retrieval practice questions, revision lessons and homeworks. This will have a significant impact on the progress of your students and produce great mathematicians who engage closely with questions, think critically and problem solve with ease.
Looking for more SSDD problems and examples? Download our resource and check out Craig Barton’s SSDD problems website: ssddproblems.com.
Need help with teaching problem solving?
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Skye – our AI maths tutor built by teachers – gives students personalised one-to-one lessons that address learning gaps and build confidence.
Since 2013 we’ve taught over 2 million hours of maths lessons to more than 170,000 students to help them become fluent, able mathematicians.
Explore our AI maths tutoring or find out about an online maths tutor for your school.