Addressing Maths Misconceptions: The 4-Stage Process To Identify And Correct Misconceptions, Tested In Over 700,000 Lessons

At Third Space Learning, we teach around 7,000 online maths lessons every week as part of our 1-to-1 maths intervention programmes. That means 7,000 opportunities for pupils to make mistakes, and for tutors to correct them. 

Mistakes come in all sorts of different forms. Some can be as simple as not reading the question properly – something we’re all familiar with! Others may arise from not understanding what is being asked, understanding the question but making a calculation error, or forgetting the method to find the answer. 

But sometimes a pupil will make a mistake that suggests a deeper lack of understanding, which can’t be solved simply by providing the correct answer in its place – a misconception. 

What is a misconception?

Consider the following example: two students are asked to word out ‘0.3 x 30’.

Student A answers as follows, showing their working: 

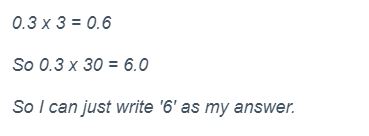
Student B answers like this: 

Both answers are wrong, but Student A has made a mistake where Student B has made a misconception. 

Student A has made a simple and relatively common multiplication error: 3 x 3 = 6 instead of 9. Their fundamental understanding of multiplying decimals by powers of 10 appears to be sound. 

Student B seems to have applied the ‘trick’ method of multiplying by 10 to the equation, and simply added a zero to the end of the correct initial calculation. This betrays a lack of understanding of the concept of multiplying decimal numbers by powers of 10 – a misconception. 

Read more: Maths Tricks or Bad Habits?

Why is it important to address misconceptions?

Calculation errors are commonplace and usually the results of ‘slips of the mind’ that are easily rectified. 

Misconceptions are different. If we only address them by quickly correcting the error they can recur and build over time, leaving pupils with significant gaps in their maths understanding that will carry on into later years (and further). 

As an example, in our online 1-to-1 SATs revision programme one of the most commonly reported misconceptions is thinking that any fraction with a larger denominator is a larger fraction. In the example below – taken from one of the lessons in our online 1-to-1 curriculum – a pupil might initially believe that both 4/7 and 2/7 are larger than 1/3 or 2/3 in this case. 

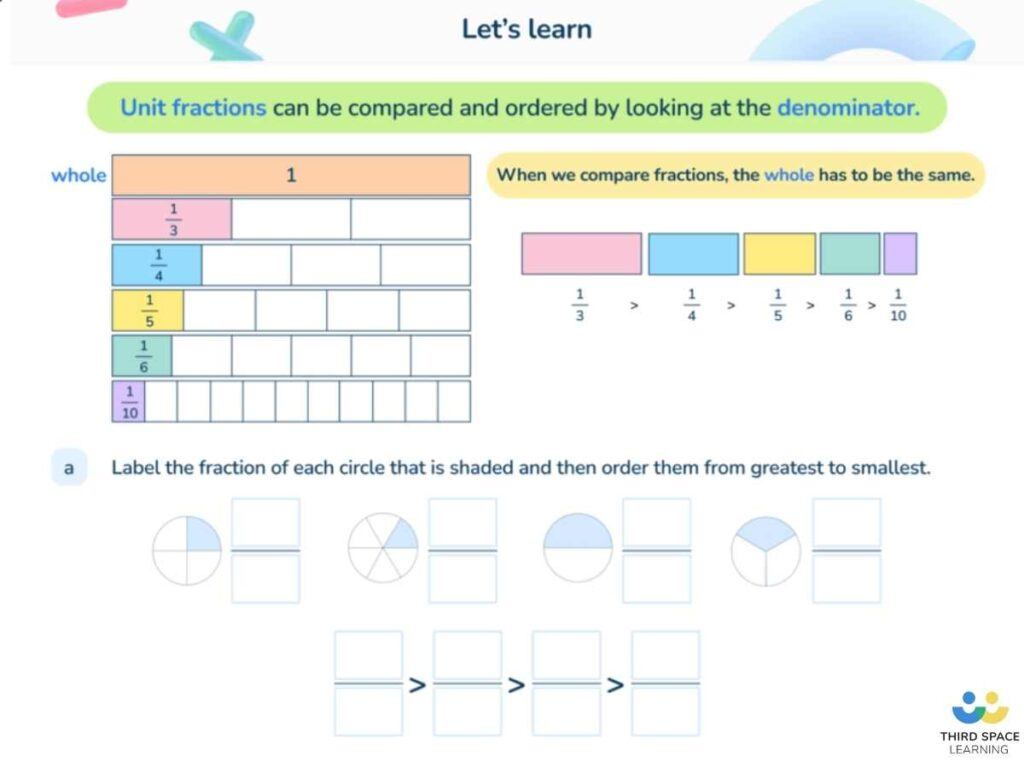
Pupils may often fall into the misconception that a larger denominator means the fraction itself is larger. This misconception actually comes from a Year 3 topic; it is a gap in their knowledge that they have carried almost to the KS2 SATs. Without being addressed, it might even cost them several marks in the exams!

When misconceptions like these arise our tutors need to be able to address not only their result, but also the misconception itself; this is the only way to ensure the gap in pupils’ maths knowledge is filled. 

Why Third Space Learning’s maths interventions are a great way of addressing pupil misconceptions

We include a module in our tutor training programme specifically on addressing misconceptions, equipping tutors with the tools they need to help their pupils overcome knowledge gaps. 

Our programmes cover every aspect of effective tutoring – from delivery, to effectively imparting subject knowledge, to pupil encouragement techniques and promoting pupil voice – ensuring they are able to provide the best teaching possible for our intervention pupils.

Moreover our tutors are ideally suited to address misconceptions; they work one-on-one with pupils in sessions lasting up to one hour, where the pupil is their sole focus. Tutor and pupil can work through problems in a way that is difficult for teachers in classrooms of around 30 pupils, ensuring that each pupil’s specific misconceptions are addressed. 

How our tutors tackle misconceptions

With thousands of lessons under our belt and plenty of experience identifying and addressing misconceptions, we’ve identified a distinct process for identifying and tackling misconceptions, comprised of four stages: preparation, investigation, addressing, and assessing – and this is what we train our tutors to do. 

N.B. While we refer to what our tutors do in each of these stages, most of the content here can also be used by class teachers/TA’s etc. 

Stage 1: Make sure you’re ready to identify misconceptions when they arise. 

Before trying to fix a misconception, you need to be able to spot one. You can make this easier on yourself by: 

• Reading up on common misconceptions for the topic you’ll cover before teaching. 
• Establishing an environment that encourages pupils to articulate their thinking and feel comfortable with making mistakes. 

As part of our online 1-to-1 interventions we have pupils sit an initial Diagnostic Assessment consisting of a series of multiple choice questions on various maths topics. 

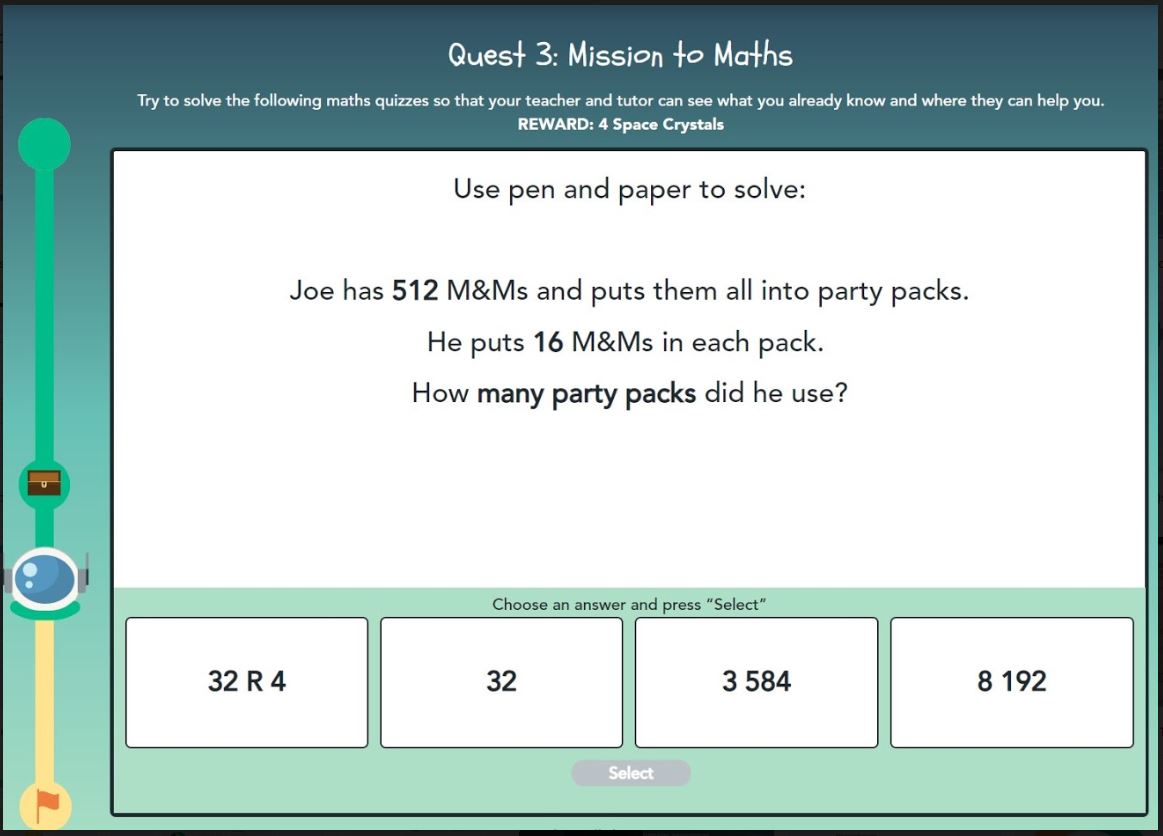
Each question includes one correct answer and three distractors, carefully designed to highlight specific misconceptions a pupil may have about each topic. This means tutors have an awareness of every pupil’s potential misconceptions before they even start teaching, and are prepared to address them if they appear during the lesson. 

We ensure our tutors can correctly address misconceptions by first ensuring that they’re subject experts. Not only do we hire from applicants with a STEM background, we provide them with further National Curriculum-aligned training to develop a strong subject knowledge base from which to base their tutoring.

We also provide tutors with in-house CPD on spotting and correcting common misconceptions, supplemented by concept-related videos in their online training portal, to refresh their memories ahead of lessons. They also spend time analysing and peer-reviewing lessons to help them pinpoint those moments where things start to go wrong in a pupil’s understanding.

Stage 2: Investigation

This step is about identifying when a misconception has been made. In order to establish this, our tutors: 

• Identify the initial mistake that was made (e.g. the wrong answer to a word problem). 
• Facilitate a discussion about the mistake, focusing on having the pupil explain their thinking e.g. by asking questions such as “How did you come up with that answer?” and “Why do you think it’s correct?” This clears up whether the error was a simple case of ‘slip of the mind’, or a misconception. 
  • N.B. Our tutors also encourage pupils to explain their reasoning even when they get an answer right; sometimes misconceptions can occur without affecting the specific problem being solved.
• Use further questioning to find the specific knowledge gaps the pupil has; this ensures they are addressing the correct misconception(s).

1-to-1 tutoring means this stage – often one that can take time in a full 30-pupil classroom – occurs quickly and easily, ensuring misconceptions can be properly addressed in a more timely manner. 

Stage 3: Addressing the misconception

It’s here that tutors actually set about ‘filling’ the knowledge gap. The exact method for this will depend on the topic; for example a misconception about rounding may be best dealt with by using a number line to visually present the concept. Some of the more common misconceptions in primary school maths are explored below. 

Where a misconception is relatively small, we encourage our tutors to deal with it immediately. However, it’s important to adapt to each situation based on the resources available. 

If a child expresses a misconception during the warm-up activity for example, and the related topic will be covered in the main body of the lesson, the tutor may model the correct answer and highlight that a misconception has been made. 

They will then address the misconception more thoroughly when it comes up later in the lesson. This way the pupil is aware of their misconception and the fact that it will be addressed, but valuable time is not spent on something that may well be dealt with in the natural progression of the lesson.

Stage 4: Assessing Learning

In the same manner as any new topic being learnt, tutors will gauge a pupil’s understanding of the material (and therefore whether they have addressed the misconception sufficiently) through assessment. 

In the case of misconceptions, assessment is simple enough: ask the pupil a similar style of question to the original, or else ask them to re-explain the concept you’ve just been discussing back to you.

If the misconception remains or if the pupil expresses confusion it is important to once again investigate their knowledge gaps related to this topic; we want to establish roughly how much time we will need to dedicate to teaching this. 

Three Common Misconceptions and How To Address Them

Misconception 1: Using addition to solve subtraction

We spend a lot of time teaching addition and then spend much less time teaching subtraction. With this in mind it’s no wonder that pupils often revert to using addition when faced with a subtraction question. 

One of the best ways to overcome this misconception by teaching the part, part, whole model; where the underlying model of both addition and subtraction are clear.

This is much better than rushing through using examples with bigger and bigger numbers, as it means children really understand how subtraction and addition fit together.

It is much better if a child really understands that 5-2=3 and how this relates to 3+2=5 and 5-3=2 and 2+3=5 than if a child can do equations with numbers to 20.

Misconception 2: Understanding money through 1-to-1 correspondence

One-to-one correspondence is one of the key maths concepts we teach at the early years level, and is central to many of the topics we teach in primary school. But when we introduce money we run the risk of confusing children – the idea that one coin could represent 10 of another can be very difficult for pupils to grasp.   

One practical solution is getting children to see how heavy, awkward and fiddly carrying lots of 1p coins around is. We can then show them how larger denominations of coins are a helpful solution to this problem – one 10p coin being much easier to carry around than 10 1p coins, for example. 

This can even be represented visually; during our online interventions tutors may use images of coins in much the same way we might use real coins – after all, 20 1p coins take up a lot more space on a screen than a single 20p coin! 

Misconception 3: Confusing square numbers with multiples of 2

The superscript 2 in square numbers is a recipe for confusion; pupils can very easily fall into the trap of assuming this means multiplying by two. Address this head on and use cubes to show 3 x 2 as well as 3², and discuss how these are different.

In our one-to-one online interventions our tutors make use of pictures of cubes for much the same purpose, as well as using multiplication grids etc. 

It’s important not to rush through this: repeat the discussion for lots of different examples to ensure pupils are secure in their understanding.  This technique of showing non examples as well as examples is another really good way of building deep understanding within a new schema.

Read more: Common Primary Maths Misconceptions

---

Misconceptions can grow to become serious hindrances to pupils’ maths progress if they are left unaddressed, but it is often extremely difficult (if not outright impossible) for class teachers to cover every pupil’s misconceptions in class. 

That’s why we’ve trained our tutors to be able to identify and rectify maths misconceptions when they encounter them during one-to-one interventions. We help plug gaps in pupil knowledge to ensure they can make progress – in class, in SATs and beyond!