High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Addition and subtraction Multiplication and division Fractions Fractions operations Decimals Order of operations

Math resources Number and quantity Arithmetic

Two step word problems

Two-step word problems

Here you will learn about two-step word problems, including how to solve a two-step word problem, how to represent these problems using equations, and how to assess the reasonableness of answers.

Students will first learn about two-step word problems as part of operations and algebraic thinking in $3$ rd grade and will continue using this skill throughout elementary and middle school.

What are two-step word problems?

Two-step word problems are word problems or story problems that require two steps to find the answer. These two steps can involve the same operation or two different operations.

To solve a two-step word problem, you must read the problem carefully before identifying each of the two steps. After identifying the two steps, you can write an equation for each step. Then you will need to solve each equation in order before arriving at the final answer.

For example,

Sarah had $\$15.$ She spent $\$8$ on a new book. Then her mom gave her $\$5.$ How much money does she have now?

We can break down the problem into steps and write an equation.

Sarah starts with $\$15,$ so this is the starting number.

Then she spends $\$8$ on a new book. This means you need to subtract $\$8.$ This is step one.

\$15-\$8 = x

$x$ represents the amount of money Sarah has after buying the book.

\$15-\$8=\$7

Next, Sarah receives $\$5$ from her mom. This needs to be added to the remaining amount from step one. This is step two.

\$7 + 5 = t

$t$ represents the total of money Sarah has after her mom gave her $\$5$ .

\$7+5=\$12

Sarah has $\$12$ now.

You can also write an equation showing both steps and use the order of operations rules to solve.

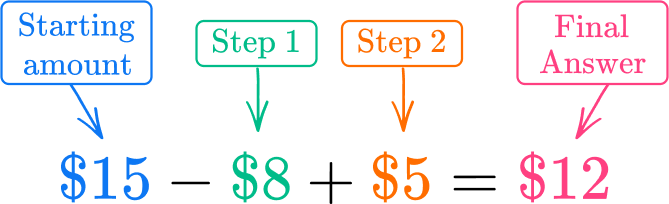
After solving the problem, you should ask yourself: Is my answer reasonable?

You can use quick mental math or estimation to see if your answer is reasonable.

You can round the $\$8$ to $\$10$ to make the estimation easier.

$\$15-\$10 + \$5 = \$10,$ so Sarah has about $\$10$ left. This means the answer of $\$12$ is reasonable.

What are two-step word problems?

[FREE] Arithmetic Worksheet (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of arithmetic. 10+ questions with answers covering a range of 4th, 5th and 6th grade topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Arithmetic Worksheet (Grade 4 to 6)

DOWNLOAD FREE

Common Core State Standards

How does this relate to $3$ rd grade math and $4$ th grade math?

Grade 3 – Operations and Algebraic Thinking (3.OA.D.8)
Solve two-step word problems using the four operations. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.

Grade 4 – Operations and Algebraic Thinking (4.OA.A.3)
Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.

How to solve two-step word problems

In order to solve two-step word problems:

Identify the first step and write an equation.
Identify the second step and write an equation.
Solve the equations in order.
Assess the reasonableness of your answer.

Two-step word problems examples

Example 1: two-step addition (same operation)

Hannah bought $2$ bags of candy for trick-or-treaters. One bag had $78$ pieces of candy and the other had $92$ pieces of candy. Hannah’s friend came over and dumped another bag of candy in the bowl. This bag had $124$ pieces of candy. How many pieces of candy are in the bowl altogether?

Identify the first step and write an equation.

First, you need to find out the total number of pieces Hannah dumped into the bowl from her two bags.

78+92=x

2Identify the second step and write an equation.

Next, you need to add the total pieces that Hannah’s friend dumped into Hannah’s total from the previous step.

x+124=c

3Solve the equations in order.

78 + 92 = 170

170 + 124 = 294

There are a total of $294$ pieces of candy in the bowl.

4Assess the reasonableness of your answer.

You can use mental math or estimation to see if your answer is reasonable.

You can quickly round each number to $100,$ which gives you a total of $300$ pieces of candy. This is close to the actual answer of $294,$ so the answer is reasonable.

Example 2: two-step problem (different operation)

A teacher ordered $8$ new boxes of pencils for her classroom. Each box of pencils had $16$ pencils. She decided to combine all of the pencils, and then split them evenly between the $4$ student tables in the room. How many pencils will each table get?

Identify the first step and write an equation.

First, you need to find the total number of pencils in all the boxes.

$8 \times 16=x$

Identify the second step and write an equation.

Next, you need to divide the total number of pencils by the number of tables.

$x \div 4=p$

Solve the equations in order.

\begin{aligned} & 8 \times 16=128 \\\\ & 128 \div 4=32 \end{aligned}

Each table will get $32$ pencils.

Assess the reasonableness of your answer.

You can use mental math or estimation to see if your answer is reasonable.

$8 \times 20=$ about $160$ total pencils divided by $4$ tables $=$ about $40$ pencils on each table. So the answer of $32$ is reasonable.

Example 3: solving two-step word problems with fractions

A cookie recipe calls for $\cfrac{1}{2}$ cup of white sugar and $\cfrac{3}{4}$ cup of brown sugar.

The baker is making $6$ batches of cookies. What is the total amount of sugar (white and brown) that will be used?

Identify the first step and write an equation.

First, you need to add the amounts of sugar to find the total amount of sugar needed for $1$ batch.

$\cfrac{1}{2}+\cfrac{3}{4}=x$

Identify the second step and write an equation.

Next, you need to multiply the total amount of sugar by the number of batches being made.

$x \times 6=s$

Solve the equations in order.

\begin{aligned} &\cfrac{1}{2}+\cfrac{3}{4}=1 \cfrac{1}{4} \\\\ &1 \cfrac{1}{4} \times 6=7 \cfrac{1}{2} \end{aligned}

$7 \cfrac{1}{2}$ total cups of sugar will be needed for $6$ batches of cookies.

Assess the reasonableness of your answer.

You can use mental math or estimation to see if your answer is reasonable.

$\cfrac{1}{2}$ and $\cfrac{3}{4}$ is a little more than $1$ cup.

Since there will be $6,$ the answer will be more than $6$ cups.

Therefore, the answer of $7 \cfrac{1}{2}$ cups is reasonable.

Example 4: solving two-step word problems with decimals

Chris makes $\$12.50$ an hour at his job at the roller skating rink. He worked $25$ hours. After he got his paycheck, he spent $\$65$ on a new pair of shoes. How much money does he have left from his paycheck?

Identify the first step and write an equation.

First, you need to find out how much money Chris’s paycheck was by multiplying the hourly rate by the number of hours he worked.

$12.50 \times 25=x$

Identify the second step and write an equation.

Next, you need to subtract $\$65$ from the total paycheck amount.

$x-65=m$

Solve the equations in order.

\begin{aligned} &12.50 \times 25=312.50 \\\\ &312.50-65=247.50 \end{aligned}

Chris has $\$247.50$ left from his paycheck.

Assess the reasonableness of your answer.

You can use mental math or estimation to see if your answer is reasonable.

To estimate the amount of Chris’s paycheck, you can multiply $12$ by $25.$ You could also multiply $12$ by $30,$ but note this will be a high estimate.

$12 \times 25=300-65 = \$235$ which makes $\$247.50$ a reasonable answer.

Example 5: interpreting remainders in two-step division word problem

Five $5$ th grade classes each have $24$ students and $2$ teachers attending a field trip. Each bus can hold $48$ people. How many buses are needed to carry all of the students and teachers to the field trip?

Identify the first step and write an equation.

First, you need to find out how many students and teachers are attending the field trip altogether. To do this, you will need to multiply $5 \times 26.$

$5 \times 26=x$

Identify the second step and write an equation.

Next, you need to divide the total number of people by the number of people each bus can carry.

$x \div 48=b$

Solve the equations in order.

Now that you have identified the steps, you can solve the equations in order.

\begin{aligned} & 5 \times 26=130 \\\\ & 130 \div 48=2 \; R \, 34 \end{aligned}

For this problem, you will need to refer back to the question in order to interpret the remainder. It asks: How many buses are needed to carry all of the students and teachers to the field trip?

So in this word problem, the answer $2 \; R \, 34$ represents $2$ full buses with $34$ people leftover. Since those $34$ people also need a bus to ride to the field trip, you would round up the answer to $3$ so that all people can attend the field trip.

$3$ buses are needed to carry all of the students and teachers to the field trip.

Assess the reasonableness of your answer.

You can use mental math or estimation to see if your answer is reasonable.

There are about $125$ people attending the field trip (about $25$ people $\times 5$ classes) and about $50$ people can fit on a bus. $125 \div 50=2.5,$ so the answer of $3$ buses is reasonable.

Example 6: interpreting remainders in two-step division word problems

Haruki had $39$ books. He got $7$ more books for his birthday. His bookshelf has $4$ shelves. He wants to put the same number of books on each shelf and put the remaining books on top of his bookshelf. How many books will go on top of Haruki’s bookshelf?

Identify the first step and write an equation.

First, you need to determine how many books Haruki has altogether.

So step $1$ is to add to find the total number of books.

$39+7=x$

Identify the second step and write an equation.

Next, you will need to divide the total number of books by the number of shelves Haruki has.

$x \div 4=b$

Solve the equations in order.

Now that you have identified the steps, you can solve the equations in order.

\begin{aligned} & 39+7=46 \\\\ & 46 \div 4=11 \mathrm~{R} 2 \end{aligned}

For this problem, you will need to refer back to the question in order to interpret the remainder. It asks: How many books will go on top of Haruki’s bookshelf?

So in this word problem, the remainder is your answer.

$2$ books will go on top of Haruki’s bookshelf.

Assess the reasonableness of your answer.

You can use mental math or estimation to see if your answer is reasonable.

Haruki has about $45$ books that he wants to divide equally between $4$ shelves, which means there would be about $11$ books on each shelf with about $1$ left over. So the answer of $2$ books is reasonable.

Teaching tips for two-step word problems

Begin with simple $2$ -step word problems on math worksheets that involve familiar situations and basic operations. Gradually increase the complexity as learners gain confidence and understanding.

Lesson plans should involve step-by-step problem-solving strategies, such as underlining important information, identifying keywords, and breaking the problem into smaller parts. Model how to solve each step before tackling the problem as a whole.

Connect math word problems to real-life scenarios that are relevant and interesting to students. This can help them see the practical application of math and reasoning skills and increase engagement on word problem worksheets.

Provide students with a template if needed to help them break down the problem into steps. You can also provide students with a printable answer key to check their work. If their answers do not match, they can go back to investigate and find the correct steps.

Start with simple two-step word problems with $1$ -digit numbers to allow students to focus on identifying the two steps. Then advance to $2$ -digit and $3$ -digit problems.

Easy mistakes to make

Incorrect order of operations
Students might perform operations in the wrong order, leading to incorrect solutions. It is imperative that students write their equations correctly to ensure the operations are performed in the correct order.

Not checking the solution
Sometimes, students may not take the time to review their solution to ensure it makes sense in the context of the problem. Checking the answer against the problem statement or using estimation to verify reasonableness can help catch errors.

Missing a step or performing the steps in the wrong order
Sometimes, students may misinterpret the problem statement, causing them to miss a step or mix up the order of steps. It’s crucial to carefully read and understand what the problem is asking for before attempting to solve it.

Practice two-step word problem questions

\$304

\$192

\$382

\$202

This is a two-step subtraction word problem, meaning each of the two steps involves subtraction.

$1$ st step: Subtract the amount spent on the phone bill.

$2$ nd step: Subtract the amount spent at dinner from what is left after step $1.$

\begin{aligned} & \$ 287-\$ 56=\$ 231 \\\\ & \$ 231-\$ 39=\$ 192 \end{aligned}

$154$ marbles

$190$ marbles

$136$ marbles

$100$ marbles

This two-step word problem involves two different operations.

$1$ st step: Subtract the number of marbles Elliot lost.

$2$ nd step: Add the number of marbles Elliot bought to the total remaining marbles from step $1.$

145-18 = 127

$127 + 27 = 154$ marbles

$42$ bags

$6$ bags

$48$ bags

$7$ bags

This two-step word problem involves two different operations.

$1$ st step: Find the total number of cookies Mrs. Smith baked.

$2$ nd step: Divide the total number of cookies by the number of cookies per bag to find the total number of bags.

24+18=42

$42 \div 6=7$ bags

\$78

\$62

\$25.50

\$9.50

This two-step word problem involves two different operations. Also note that there is an extra bit of unnecessary information in the word problem (Sarah has $15$ comic books).

$1$ st step: Determine the total cost of the comic books Sarah buys.

$2$ nd step: Add the amount spent on the poster to the total from step $1.$

\begin{aligned} & \$ 3.50 \times 5=\$ 17.50 \\\\ & \$ 17.50+\$ 8=\$ 25.50 \end{aligned}

\$748

\$52

\$359

\$42

This two-step word problem involves two different operations.

$1$ st step: Multiply to find the amount Libby earned from selling $29$ boxes of cookies.

$2$ nd step: Determine how much more money Libby needs to earn to reach her goal by subtracting the total from step $1$ from her goal amount.

\begin{aligned} & 29 \times \$ 12=\$ 348 \\\\ & \$ 400-\$ 348=\$ 52 \end{aligned}

15 \mathrm{R}4

16

15

15 \cfrac{4}{7}

This two-step word problem involves two different operations.

$1$ st step: Subtract to find the number of fossils remaining after donating to the museum.

$2$ nd step: Determine how many fossils Georgio can put on each shelf by dividing the remaining fossils by the number of shelves.

\begin{aligned} & 128-19=109 \\\\ & 109 \div 7=15 \mathrm{R} 4 \end{aligned}

Two-step word problems FAQs

What are two-step word problems?

Two-step word problems are word problems or story problems that require two steps to find the answer. These two steps can involve the same operation or two different operations.

How do I solve a two-step word problem?

To solve a two-step word problem, you must read the problem carefully before identifying each of the two steps. After identifying the two steps, you can write an equation. Then you will need to perform each step in the correct order before arriving at the final answer.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.